Самостоятельная работа по теме решение задач с помощью систем уравнений ответы

Самостоятельная работа по теме: «Решение задач с помощью систем уравнений». Работа представлена в двух вариантах с ответами. Дидактические материалы по алгебре для 7 класса./ Б. Г.Зив, В. А. Гольдич

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Скачать:

Видео:Урок по теме РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ СИСТЕМЫ УРАВНЕНИЙ 7 КЛАСССкачать

Предварительный просмотр:

1. Скорость теплохода по течению реки 45,2 км/ч, а против течения – 36, 2 км/ч. Найдите скорость течения реки.
2. Из А в В ( АВ = 18 км) вышел турист. Через 1,5 ч из В ему на встречу вышел другой турист, и они встретились через 1 ч 20 мин. Если бы они вышли одновременно, то встретились бы через 2 ч. Какова скорость каждого туриста?

1. Сумма двух чисел равна 98, а разность 42,4. Найдите эти числа.
2. Автомобиль за 3,5 ч проехал на 10 км больше, чем мотоциклист за 2,5 ч. Скорость мотоциклиста на 20 км/ч больше скорости автомобиля. Найдите скорость автомобиля и мотоциклиста.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

По теме: методические разработки, презентации и конспекты

Урок математики (алгебры) по теме: «Решение задач с помощью систем уравнений второй степени».

Урок математики (алгебры) по теме: «Решение задач с помощью систем уравнений второй степени». Урок для учащихся 9 класса. Применение индивидуальных карточек на уроке помогает учащимся решать самостоят.

Решение задач с помощью систем уравнений с двумя переменными второй степени.

Презентация к уроку по математике 9 класс. Задачи на совместную работу и на использование формулы двузначного числа.

Алгоритмы решения задач с помощью систем уравнений

В курсе алгебры 9 класса отводится всего 4 часа на решение задач с помощью систем уравнений второй степени. Это задачи на движение, совместную работу и задачи с геометрическим содержанием. Для каждого.

Решение задач с помощью систем уравнений

Презентация «Решение задач с помощью систем уравнений», подготовленная по учебнику «Алгебра. 7 класс. Макарычев Ю.Н.». Прекрасно подходит учителям математики для использования на уроках. СКАЧАТЬ.

«Решение задач с помощью систем уравнений и систем неравенств»

Урок математики в 9 классе на тему «Решение задач с помощью систем уравнений и систем неравенств».

Решение задач с помощью систем уравнений с двумя переменными.

Урок изучения нового материала в 9 классе.

Решение задач с помощью систем уравнений второй степени. 9 класс . план-конспект.

План — конспект «Решение задач с помощью систем уравнений второй степени» составлен на основе требований ФГОС по математике для 9 класса. Урок познования нового материала с применением про.

Видео:Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Самостоятельная работа «Решение задач с помощью систем уравнени»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 1

1. Задуманы два натуральных числа. Найдите эти числа, если их произведение равно 48, а их сумма равна 16.

2. Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого

3. Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов. Найдите их скорости, если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 2

1.Задуманы два натуральных числа. Найдите числа, если их частное равно 3, а их разность равна 6.

2.Известно что, два карандаша и три тетради стоят 35 рублей, а две тетради и три карандаша стоят 40 рублей. Необходимо выяснить, сколько стоят пять карандашей и шесть тетрадей.

3.Разность катетов прямоугольного треугольника равна 23 см, а его гипотенуза равна 37 см. Найдите площадь треугольника.

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 1

1. Задуманы два натуральных числа. Найдите эти числа, если их произведение равно 48, а их сумма равна 16.

2. Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого

3. Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов. Найдите их скорости, если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 2

1.Задуманы два натуральных числа. Найдите числа, если их частное равно 3, а их разность равна 6.

2.Известно что, два карандаша и три тетради стоят 35 рублей, а две тетради и три карандаша стоят 40 рублей. Необходимо выяснить, сколько стоят пять карандашей и шесть тетрадей.

3.Разность катетов прямоугольного треугольника равна 23 см, а его гипотенуза равна 37 см. Найдите площадь треугольника.

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 1

1. Задуманы два натуральных числа. Найдите эти числа, если их произведение равно 48, а их сумма равна 16.

2. Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого

3. Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов. Найдите их скорости, если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

Самостоятельная работа по теме: « Решение задач с помощью систем уравнений» Вариант 2

1.Задуманы два натуральных числа. Найдите числа, если их частное равно 3, а их разность равна 6.

2.Известно что, два карандаша и три тетради стоят 35 рублей, а две тетради и три карандаша стоят 40 рублей. Необходимо выяснить, сколько стоят пять карандашей и шесть тетрадей.

3.Разность катетов прямоугольного треугольника равна 23 см, а его гипотенуза равна 37 см. Найдите площадь треугольника.

3. Обозначим скорость легковушки буквой x , а грузовика — y. Оба автомобиля проехали одно и тоже расстояние (S = vt). S = x • 3,5 и S = y • 5 ⇒ 3,5x = 5y ⇒ 3,5x – 5y = 0 .
Так же известно, что скорость лег. автомобиля на 30 км/ч больше скорости грузовика, ⇒ x = y + 30 ⇒ x – y – 30 = 0 ; скорость лег. автомобиля равна 100км/ч, а грузового — 70км/ч.

Видео:Алгоритм решения задач с помощью систем уравнений. Практическая часть. 9 класс.Скачать

Ср 8.1 Решение задач с помощью систем уравнений

Просмотр содержимого документа
«Ср 8.1 Решение задач с помощью систем уравнений»

Самостоятельная работа 8.1

Решение задач с помощью систем уравнений

А1. В первый день продали 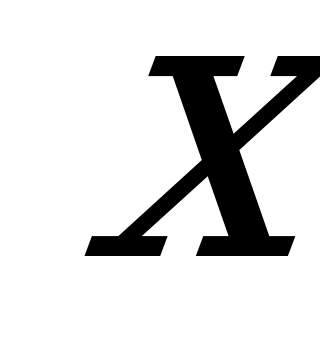кг картофеля, а во второй кг. Составьте систему уравнений с двумя переменными по следующему условию:

а) всего за два дня продали 164 кг картофеля;

б) разница между количеством картофеля, проданных в первый и второй дни , равна 18 кг.

А2. Сумма двух чисел равна 92, а их разность равна 16. Найдите эти числа.

А3. Три яблока и две груши весят вместе 1 кг 200 г, а два яблока и три груши весят 1 кг 300 г. Сколько весит яблоко и сколько весит груша?

В1. Моторная лодка прошла 63 км по течению реки и 45 км против течения, затратив на весь путь 6 ч. Найдите скорость лодки в стоячей воде и скорость течения, если известно, что, двигаясь 5 ч по течению реки, она проходит тот же путь, что за 7 ч. Против течения.

Задания А1-А3 соответствуют уровню обязательной подготовки.

Самостоятельная работа 8.1

Решение задач с помощью систем уравнений

А1. На верхней полке 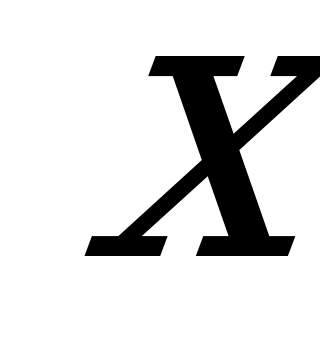книг, а на нижней книг. Составьте систему уравнений с двумя переменными по следующему условию:

а) всего на полках 112 книг;

б) на верхней полке на 36 книг больше, чем на нижней.

А2. Сумма двух чисел равна 17, а их разность равна 7. Найдите эти числа.

А3. Семь альбомов и две тетради стоят вместе 111 руб, а пять альбомов и три тетради стоят 84 руб. Сколько стоит один альбом и сколько стоит одна тетрадь?

В1. Моторная лодка прошла 63 км по течению реки и 45 км против течения, затратив на весь путь 6 ч. Найдите скорость лодки в стоячей воде и скорость течения, если известно, что, двигаясь 5 ч по течению реки, она проходит тот же путь, что за 7 ч. Против течения.

Задания А1-А3 соответствуют уровню обязательной подготовки.

Видео:Решение задач с помощью систем уравнений второй степени. Алгебра, 9 классСкачать

Самостоятельная работа по теме «Решение задач с помощью систем уравнений»

2 варианта по 3 задачи.

1. Задуманы два натуральных числа. Найдите эти числа, если их произведение равно 48, а их сумма равна 16.

2. Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если известно, что один из них на 7 см больше другого

3. Легковой автомобиль за 3,5 часа проехал то же расстояние, что и грузовой за 5 часов. Найдите их скорости, если известно, что легковой автомобиль двигался на 30 км/ч быстрее грузового.

1. Задуманы два натуральных числа. Найдите числа, если их частное равно 3, а их разность равна 6.

2. Известно что, два карандаша и три тетради стоят 35 рублей, а две тетради и три карандаша стоят 40 рублей. Необходимо выяснить, сколько стоят пять карандашей и шесть тетрадей.

3. Разность катетов прямоугольного треугольника равна 23 см, а его гипотенуза равна 37 см. Найдите площадь треугольника.

1. 12 и 4
2. 12 см, 5 см
3. 100км/ч / 70км/ч.

1. 9 и 3
2. 80 рублей
3. 210 см 2

🎦 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра 9 класс (Урок№26 - Решение задач с помощью систем уравнений второй степени.)Скачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ. §3 алгебра 7 классСкачать

Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

АЛГЕБРА 7 класс. Решение задач с помощью систем уравненийСкачать

Решение задач с помощью систем уравнений | Алгебра 7 класс #48 | ИнфоурокСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

7 класс// АЛГЕБРА // Решение задач с помощью систем уравненийСкачать

Решение задач с помощью систем уравнений, 7 классСкачать

🔥 КУДА ИДТИ УЧИТЬСЯ, ЕСЛИ ТУПОЙ?Скачать

Самостоятельная работа 4.3.Решение текстовых задач с помощью системы линейных уравненийСкачать

Решение задач с помощью систем уравнений второй степени. Урок 17. Алгебра 9 классСкачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать