Самостоятельная работа по алгебре решение уравнений в целых числах

Данная работа содержит 4 варианта самостоятельной работы по теме «Целые уравнения» с заданиями в формате ОГЭ.

Просмотр содержимого документа
«Самостоятельная работа по теме «Решение целых уравнений»»

;

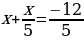
Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

(−2х + 1) ( − 2х −7) = 0;

Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

х 3 + 2х 2 – 9х – 18 = 0

(х + 3) 4 – 2(х + 3) 2 – 15 = 0

;

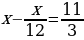
Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

х 3 + 5х 2 – х – 5 = 0

(х – 4) 4 – 4(х – 4) 2 – 21 = 0

;

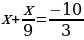
Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

(5х – 2) ( − х + 3) = 0;

Решите уравнение. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Самостоятельная работа по алгебре «Решение целых уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

ВАРИАНТ 1. Решите уравнения

А) х 3 – 5х 2 – х + 5 = 0

Б) х 4 – 2х 2 – 8 = 0

В) (х 2 – 5х)(х 2 – 5х + 10) + 24 = 0

ВАРИАНТ 2. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 – 8х 2 – 9 = 0

В) (х 2 + 4х)(х 2 + 4х – 17) + 60 = 0

ВАРИАНТ 3. Решите уравнения

А) х 3 – 7х 2 – 4х + 28 = 0

Б) х 4 – 24х 2 – 25 = 0

В) (х 2 – 2х)(х 2 – 2х – 27) + 72 = 0

ВАРИАНТ 4. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 + 5х 2 – 36 = 0

В) (х 2 – 7х )(х 2 – 7х + 22) + 120 = 0

ВАРИАНТ 1. Решите уравнения

А) х 3 – 5х 2 – х + 5 = 0

Б) х 4 – 2х 2 – 8 = 0

В) (х 2 – 5х)(х 2 – 5х + 10) + 24 = 0

ВАРИАНТ 2. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 – 8х 2 – 9 = 0

В) (х 2 + 4х)(х 2 + 4х – 17) + 60 = 0

ВАРИАНТ 3. Решите уравнения

А) х 3 – 7х 2 – 4х + 28 = 0

Б) х 4 – 24х 2 – 25 = 0

В) (х 2 – 2х)(х 2 – 2х – 27) + 72 = 0

ВАРИАНТ 4. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 + 5х 2 – 36 = 0

В) (х 2 – 7х )(х 2 – 7х + 22) + 120 = 0

ВАРИАНТ 1. Решите уравнения

А) х 3 – 5х 2 – х + 5 = 0

Б) х 4 – 2х 2 – 8 = 0

В) (х 2 – 5х)(х 2 – 5х + 10) + 24 = 0

ВАРИАНТ 2. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 – 8х 2 – 9 = 0

В) (х 2 + 4х)(х 2 + 4х – 17) + 60 = 0

ВАРИАНТ 3. Решите уравнения

А) х 3 – 7х 2 – 4х + 28 = 0

Б) х 4 – 24х 2 – 25 = 0

В) (х 2 – 2х)(х 2 – 2х – 27) + 72 = 0

ВАРИАНТ 4. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 + 5х 2 – 36 = 0

В) (х 2 – 7х )(х 2 – 7х + 22) + 120 = 0

ВАРИАНТ 1. Решите уравнения

А) х 3 – 5х 2 – х + 5 = 0

Б) х 4 – 2х 2 – 8 = 0

В) (х 2 – 5х)(х 2 – 5х + 10) + 24 = 0

ВАРИАНТ 2. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 – 8х 2 – 9 = 0

В) (х 2 + 4х)(х 2 + 4х – 17) + 60 = 0

ВАРИАНТ 3. Решите уравнения

А) х 3 – 7х 2 – 4х + 28 = 0

Б) х 4 – 24х 2 – 25 = 0

В) (х 2 – 2х)(х 2 – 2х – 27) + 72 = 0

ВАРИАНТ 4. Решите уравнения

А) х 3 + 3х 2 – 4х – 12 = 0

Б) х 4 + 5х 2 – 36 = 0

В) (х 2 – 7х )(х 2 – 7х + 22) + 120 = 0

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 861 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 51 человек из 23 регионов

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 521 материал в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

12. Целое уравнение и его корни

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 28.10.2018
• 2200
• 109

• 05.10.2018
• 470
• 5

• 11.06.2018
• 741
• 7

• 31.05.2018
• 535
• 9

• 22.04.2018
• 406
• 1

• 09.04.2018
• 471
• 13

• 03.04.2018
• 1840
• 36

• 31.03.2018
• 2175
• 34

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 06.11.2018 4330
• DOCX 16.5 кбайт
• 242 скачивания
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Гуляев Александр Фёдорович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 9 месяцев
• Подписчики: 0
• Всего просмотров: 45366
• Всего материалов: 39

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Алгебра 10 класс (Урок№9 - Решение уравнений в целых числах.)Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Около 20% детей до 15 лет не воспринимают прочитанную информацию

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Вузы РФ не будут повышать стоимость обучения на первом курсе

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Олимпиадные задания. Решение уравнений в целых числах
методическая разработка по алгебре (9, 10, 11 класс) на тему

В данной работе представлены различные способы решения уравнений в целых числах. Работа может быть использована при подготовке к олимпиадам, на кружковых и факультативных занятиях.

Видео:9 класс. Алгебра. Решение уравнений в целых числах.Скачать

Скачать:

Видео:10 класс. Алгебра. Решение уравнений в целых числахСкачать

Предварительный просмотр:

МБОУ «Высокогорская средняя общеобразовательная школа №2

Высокогорского муниципального района Республики Татарстан»

Решение уравнений в целых числах

Аксанова Ильсияр Исмагиловна

Учитель математики высшей категории

С. Высокая Гора – 2015 г.

Работа посвящена решению уравнений в целых числах. Актуальность этой темы обусловлена тем, что задачи, основанные на решении уравнений в целых числах, часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике и на ЕГЭ в старших классах. В школьной программе эта тема рассматривается в ознакомительном порядке. В работе представлены различные способы решения уравнений в целых числах, разобраны конкретные примеры. Данная работа будет полезна учителям старших классов для подготовки к ЕГЭ и олимпиадам.

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми , в честь древнегреческого математика Диофанта Аксандрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

При решении уравнений в целых и натуральных числах можно условно выделить следующие способы решения:

• способ перебора вариантов;
• применение алгоритма Евклида;
• применение цепных дробей;
• разложения на множители;
• решение уравнений в целых числах как квадратных относительно какой-либо переменной;
• метод остатков;
• метод бесконечного спуска;
• оценка выражений, входящих в уравнение.

В работе представлены два приложения: п риложение 1. Таблица остатков при делении степеней ( a n : m ); приложение 2. Задачи для самостоятельного решения

1. Способ перебора вариантов.

Пример 1.1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49 х + 51 у = 602.

Решение. Выразим из уравнения переменную х через у х = , так как х и у – натуральные числа, то

х = 602 — 51 у ≥ 49, 51 у ≤553, 1≤ у ≤10 .

Полный перебор вариантов показывает, что натуральными решениями уравнения являются х =5, у =7.

2. Применение алгоритма Евклида. Теорема.

Дано уравнение ax+by=c , где a, b, c -целые числа, a и b не равны 0.

Теорема: Если c не делится нацело на НОД( a,b ), то уравнение не разрешимо в целых числах. Если НОД( a,b )=1или c делится на НОД( a,b ), то уравнение разрешимо в целых числах. Если (x 0 , y 0 )- какое-нибудь решение уравнения, то все решения уравнения задаются формулами:

y=y 0 +at , где t — принадлежит множеству целых чисел.

Пример 2.1. Решить уравнение в целых числах 5 х + 7 у = 19

Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Тогда 5 x 0 + 7 y 0 = 19, откуда

5( х – x 0 ) + 7( у – y 0 ) = 0,

5( х – x 0 ) = –7( у – y 0 ).

Поскольку числа 5 и 7 взаимно простые, то

х – x 0 = 7 k , у – y 0 = –5 k.

Значит, общее решение:

х = 1 + 7 k , у = 2 – 5 k ,

где k – произвольное целое число.

Ответ: (1+7 k ; 2–5 k ), где k – целое число.

Пример 2.2. Решить уравнение 201 х – 1999 у = 12.

Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201 х – 1999 у = 1. Тогда пара чисел

x 0 = 1273·12 = 15276, y 0 = 128·12 = 1536

является решением уравнения 201 х – 1999 у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999 k , у = 1536 + 201 k , где k – целое число,

или, используя, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201, имеем

х = 1283 + 1999 n , у = 129 + 201 n , где n – целое число.

Ответ: (1283+1999 n , 129+201 n ), где n – целое число.

3. Метод остатков.

Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.

Замечание . Говоря строго математическим языком, для решения уравнения в данном случае применяется теория сравнений.

Рассмотрим примеры, которые раскрывают сущность данного метода.

Пример 3.1. Решить уравнение в целых числах x 3 + y 3 = 3333333;

Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в приложении 1), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

Пример 3.2. Решить уравнение в целых числах x 3 + y 3 = 4( x 2 y + xy 2 + 1).

Перепишем исходное уравнение в виде ( x + y ) 3 = 7( x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

Пример 3.3. Решить в целых числах уравнение x 2 + 1 = 3 y .

Решение. Заметим, что правая часть уравнения делится на 3 при любом целом y .

Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.По теореме о делении с остатком целое число х либо делится на 3, либо при делении на три в остатке дает 1 или 2.

Если х = 3 k , то правая часть уравнения на 3 не делится.

Если х = 3 k+ 1, то x 2 + 1= (3 k+ 1) 2 +1=3 m +2, следовательно, опять левая часть на 3 не делится.

Если х = 3 k+ 2, то x 2 + 1= (3 k+ 2) 2 +1=3 m +2, следовательно, и в этом случае левая часть уравнения на три не делится.

Таким образом, мы получили, что ни при каких целых х левая часть уравнения на 3 не делится, при том, что левая часть уравнения делится на три при любых значениях переменной y . Следовательно, уравнение в целых числах решений не имеет.

Ответ: целочисленных решений нет.

Пример 3.4. Решить в целых числах x³ — 3y³ — 9z³ = 0 (1)

Решение. Очевидно, что решением уравнения будет тройка чисел (0; 0; 0).

Выясним, имеет ли уравнение другие решения. Для этого преобразуем уравнение (1) к виду

x ³ = 3 y ³ + 9 z ³ (2)

Так как правая часть полученного уравнения делится на 3, то и левая должна делиться на три, следовательно, так как 3 — число простое, х делится на 3, т.е. х = 3 k , подставим это выражение в уравнение (2), получим:

27 k 3 = 3 y ³ + 9 z ³, откуда

9 k 3 = y ³ + 3 z ³ (3)

следовательно, y ³ делится на 3 и y = 3 m . Подставим полученное выражение в уравнение (3): 9 k 3 = 27 m ³ + 3 z ³, откуда

3 k 3 = 9 m ³ + z ³ (4)

В свою очередь, из этого уравнения следует, что z 3 делится на 3, и z = 3 n . Подставив это выражение в (4), получим, что k 3 должно делиться на 3.

Итак, оказалось, что числа, удовлетворяющие первоначальному уравнению, кратны трём, и сколько раз мы не делили бы их на 3, опять должны получаться числа, кратные трём. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0) является единственным.

4. Решение уравнений в целых числах сведением их к квадратным.

Пример 4.1. Решить в простых числах уравнение

х 2 – 7 х – 144 = у 2 – 25 у .

Решим данное уравнение как квадратное относительно переменной у . Получим: у = х + 9 или у = 16 – х .

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х , имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

Пример 4.2 . Решить в целых числах уравнение x + y = x 2 – xy + y 2 .

Рассмотрим данное уравнение как квадратное уравнение относительно x :

x 2 – ( y + 1) x + y 2 – y = 0.

Дискриминант этого уравнения равен –3 y 2 + 6 y + 1. Он положителен лишь для следующих значений у : 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х , которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

Пример 4.3 . Решить уравнение в целых числах: 5 х 2 +5 у 2 +8 ху +2 у -2 х +2=0.

Рассмотрим уравнение как квадратное относительно х:

5 х 2 + (8 у — 2) х + 5 у 2 + 2 у + 2 = 0

D = (8 у — 2) 2 — 4·5(5 у 2 + 2 у + 2) = 64 у 2 — 32 у + 4 = -100 у 2 — 40 у – 40 = = -36( у 2 + 2 у + 1) = -36( у + 1) 2

Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.

-36( у + 1) 2 = 0. Это возможно при у = -1, тогда х = 1.

5. Разложение на множители .

Пример 5.1. Решить в целых числах уравнение x 2 – xy – 2 y 2 = 7.

Разложим левую часть на множители ( x – 2 y )( x + y ) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2 y = 7, x + y = 1;

2) x – 2 y = 1, x + y = 7;

3) x – 2 y = –7, x + y = –1;

4) x – 2 y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

Пример 5.2 . Решить уравнение в целых числах: х 2 + 23 = у 2

Решение. Перепишем уравнение в виде:

у 2 — х 2 = 23, ( у — х )( у + х ) = 23

Так как х и у – целые числа и 23 – простое число, то возможны случаи:

Решая полученные системы, находим:

Пример 5.3 . Решить уравнение в целых числах y 3 — x 3 = 91.

Решение. Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:

( y — x )( y 2 + xy + x 2 ) = 91

Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91

Проводим исследование. Заметим, что для любых целых x и y число

y 2 + yx + x 2 ≥ y 2 — 2| y || x | + x 2 = (| y | — | x |) 2 ≥ 0,

следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение равносильно совокупности систем уравнений:

Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.

Пример 5.4 . Решить в целых числах уравнение x + y = xy .

Решение. Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1)

x + y – xy – 1 = – 1

Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: ( x — 1)( y — 1) = 1

Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1). Записав соответствующие системы уравнений и, решив их, получим решение исходного уравнения.

Пример 5.5 . Доказать, что уравнение ( x — y ) 3 + ( y — z ) 3 + ( z — x ) 3 = 30 не имеет решений в целых числах.

Решение. Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:

( x — y )( y — z )( z — x ) = 10

Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

6. Метод бесконечного спуска.

Метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.

Пример 6.1 . Решить уравнение в целых числах 5 x + 8 y = 39.

Выберем неизвестное, имеющее наименьший коэффициент , и выразим его через другое неизвестное: . Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3 y без остатка делится на 5.

Введем дополнительную целочисленную переменную z следующим образом: 4 –3 y = 5 z . В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами. Решать его будем уже относительно переменной y , рассуждая аналогично: . Выделяя целую часть, получим:

Рассуждая аналогично предыдущему, вводим новую переменную

Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z : = . Требуя, чтобы было целым, получим: 1 – u = 2 v , откуда u = 1 – 2 v . Дробей больше нет, спуск закончен.

Теперь необходимо «подняться вверх». Выразим через переменную v сначала z , потом y и затем x :

z = = = 3 v – 1; = 3 – 5 v .

Формулы x = 3+8 v и y = 3 – 5 v , где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.

Ответ: x = 3+8 v и y = 3 – 5 v.

7. Оценка выражений, входящих в уравнение.

Пример 7.1. Решить в целых числах уравнение ( х 2 + 4)( у 2 + 1) = 8ху

Решение. Заметим, что если ( х ;у ) – решение уравнения, то (- х ;- у ) – тоже решение.

И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:

Пусть х > 0, у > 0, тогда, согласно неравенству Коши,

тогда их произведение ( х + )( у + ) = 4·2 = 8, значит, х + = 4 и у + = 2.

Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.

Пример 7.2 . Решить уравнение в целых числах

x 2 + 13 y 2 – 6 xy = 100

Решение . x 2 + 13 y 2 –6 xy= 100 ↔ ( x- 3 y ) 2 + 4 y 2 = 100 . Так как ( x- 3 y ) 2 ≥ 0 , то 4 y 2 ≤ 100 , или │ 2 y│≤ 10 . Аналогично, в силу 4 y 2 ≥ 0 должно выполняться │x- 3 y│≤ 10 .

📹 Видео

Решите уравнение в целых числах x^3-10x^2+yx-y=0 ★ Диофантовы уравнения ★ Как решать?Скачать

Решение уравнений в целых числахСкачать

16. Решение линейных уравнений в целых числах. Часть 1. Алексей Савватеев. 100 уроков математикиСкачать

Уравнение в целых числах.Скачать

2 урок. Решение уравнений в целых числах.Скачать

Решите уравнение в целых числах 3x^2+5y^2=345 ✱ Диофантовы уравнения ✱ Как решать?Скачать

Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

Уравнение с двумя неизвестными. Решить в целых числах. ЗадачаСкачать

Решите уравнение в целых числах ➜ x²-y²=2023Скачать

Решить уравнение в целых числахСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Как решать уравнения с двумя переменными в целых числах! Лёгкий способ!Скачать

Решите уравнение в целых числах ➜ 2x^2+xy=x+7Скачать

Целое уравнение и его корни. Алгебра, 9 классСкачать