Данная самостоятельная работа позволит отработать навык решения целых уравнений (метов вынесения общего множителя, замена переменной). Учителю — выявить пробелы по данной теме
- Просмотр содержимого документа «Самостоятельная работа «Уравнения с одной переменной»»
- Самостоятельная работа по теме «Интегрирование методом замены переменной»
- Методы решения систем уравнений с двумя переменными
- п.1. Метод подстановки
- п.2. Метод сложения
- п.3. Метод замены переменных
- п.4. Графический метод
- п.5. Примеры
- 🌟 Видео
Просмотр содержимого документа
«Самостоятельная работа «Уравнения с одной переменной»»
Самостоятельная работа «Уравнения с одной переменной»
Видео:Решение уравнения методом замены переменнойСкачать

Самостоятельная работа по теме «Интегрирование методом замены переменной»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
Вычисление неопределенных интегралов методом введения новой переменной .
Цель работы : овладение методом введения новой переменной.
для вычисления интегралов.
Умение и навыки, которые должны приобрести студенты: самостоятельно вычислять интегралы.
Рекомендации по выполнению .
1.Разобрать решение примеров.
2.Выполнить задания тренажера , используя указания.
3.Оформить решение задач тренажера в тетради.
Определение. Дифференцируемая функция F ( x ) называется первообразной функции f ( x ) на заданном промежутке, если для всех x из этого промежутка справедливо равенство: F ’( x )= f ( x ).
Теорема. Если функция F ( x ) является первообразной функции f ( x ) на некотором промежутке, то множество всех первообразных этой функции имеет вид F ( x )+С, где С – любое действительное число.
Определение. Совокупность всех первообразных F ( x )+С функции f ( x ) на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом 
Таким образом, если F ( x ) – какая-нибудь первообразная функции f ( x ) на некотором промежутке, то 
Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной: отсюда происходит и само название «неопределенный интеграл».
Свойства неопределенного интеграла:
1. 

2.
3.
Таблица неопределенных интегралов дана в конспекте.
Алгоритм интегрирования методом замены переменной:
1. Определить, к какому табличному интегралу приводится данный интеграл.
2. Определить, какую часть подынтегральной функции заменить новой переменной, и записать эту замену.
3. Найти дифференциалы обеих частей замены и выразить дифференциал старой переменной через дифференциал новой переменной.
4. Произвести замену под интегралом.
5. Найти полученный интеграл по таблице.
6. В результате произвести обратную замену, т.е. перейти к старой переменной. Результат полезно проверить дифференцированием.
Пример : 



В простых случаях введение новой переменной u рекомендуется выполнять в уме, применяя следующие преобразования дифференциала dx :

Cos x dx=d(sinx);
И обозначая мысленно выражение в скобка через u . Такой прием интегрирования называют непосредственным.
1 . ∫ cos 3 x dx . 2. ∫ sin 
Указание. Пример 1 можно решить двумя способами: 1) положив 3 x = u , x = u /3, dx = du /3; 2)приведя интеграл к виду 
1. ∫ e -3 x dx . 2. ∫ 
1. ∫( e x /2 + e — x /2 ) dx . 2. ∫ 
3. ∫(3-2 x ) 4 dx . 4. ∫ 
5. ∫ 
7. ∫ 

Указание. Примеры решаются по формуле:
∫ 
Т.е. если числитель подынтегральный дроби есть производная от знаменателя, то интеграл равен логорифму знаменателя.
1. ∫ 

3. ∫ctg x dx . 4. ∫tg x dx.
5. 

7. 

9. ∫ sin 2 x cosx dx. 10. ∫ cos 3 x sinx dx .
Указание. Примеры можно решить подстановкой sinx = u или непосредственно, заменив cosx dx через d ( sinx ).
1. 
3. 
5. 
Указание . Примеры можно решить подстановкой x 3 = u или непосредственно, заменив x 2 dx через 
1. 

2. 

3. 

4. 
5. 
6. 
Оформить решение примеров в тетради .
По результатам решения тренажера выставляется оценка, которая учитывается при приеме дифференцированного зачета.
Шкала оценки образовательных достижений
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Методы решения систем уравнений с двумя переменными
п.1. Метод подстановки
Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.
Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.
п.2. Метод сложения
п.3. Метод замены переменных
Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.
п.4. Графический метод
Графический метод подробно рассмотрен в §15 данного справочника.
п.5. Примеры
Пример 1. Решите систему уравнений:
а) ( left< begin mathrm & \ mathrm & endright. )
Решаем методом подстановки: ( left< begin mathrm & \ mathrm & endright. )
Для нижнего уравнения: ( mathrm )
Подставляем в верхнее уравнение: ( mathrm )
б) ( left< begin mathrm & \ mathrm & endright. )
Замена переменных: ( left< begin mathrm & \ mathrm & endright. )
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: ( left< begin mathrm & \ mathrm & endright.Rightarrow left< begin mathrm & \ mathrm & endright. )
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ mathrm< D=9^2-4cdot 2cdot 10=1, b=frac> = left[begin mathrm & \ mathrm & endright. $$ Возвращаемся к исходным переменным: ( left[begin left<begin mathrm & \ mathrm & endright.& \ left<begin mathrm & \ mathrm & endright. endright. )
🌟 Видео
Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

8 класс "Решение уравнений методом замены переменной"Скачать

9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Решение уравнений методом замены переменной.Скачать

решение уравнения с заменой переменнойСкачать
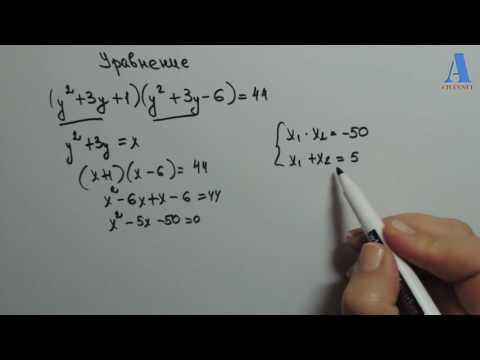
МЕРЗЛЯК-6 САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ТЕМЕ РЕШЕНИЕ УРАВНЕНИЙ ПАРАГРАФ-41Скачать

Решение биквадратных уравнений. 8 класс.Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение систем уравнений методом подстановкиСкачать

решение уравнений методом замены переменных 1Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Математический анализ, 20 урок, Метод замены переменнойСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Пример 47. Решить систему методом замены переменнойСкачать

Как решать уравнения с дробью? #shortsСкачать

Система уравнений. Метод алгебраического сложенияСкачать














