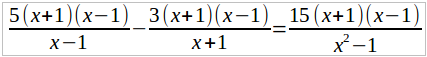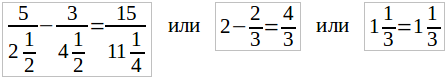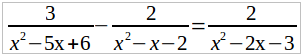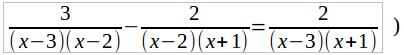Самое сложное уравнение в мире и ответ на него

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

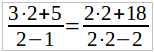
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Почему самые сложные уравнения физики такие трудные?

Уравнения Навье-Стокса описывают простые повседневные явления, вроде воды, текущей из садового шланга — однако на них основана задача, решение которой оценили в миллион долларов

В физике есть уравнения, описывающие всё, от растяжения пространства-времени до полёта фотона. Однако же лишь один набор уравнений считается настолько математически сложным, что его выбрали в роли одной из семи «Задач тысячелетия», за решение которых Математический институт Клэя предлагает премию в миллион долларов: это уравнения Навье-Стокса, описывающие течение жидкостей.

Недавно я писал о том, как для этих уравнений был получен новый важный результат. И эта работа свидетельствует о том, что прогресс на пути к «премии тысячелетия» будет более тяжёлым, чем ожидалось. Почему же эти уравнения, описывающие такие знакомые явления, как вода, текущая по шлангу, математически понять гораздо сложнее, чем, допустим, уравнения поля Эйнштейна, включающие в себя такие ошеломляющие объекты, как чёрные дыры?

Ответ, как я понял, кроется в турбулентности. Это явление испытывали мы все, в полёте в неоднородном воздухе на высоте в 10 000 м, или при наблюдении за воронкой от уходящей в слив воды в ванне. Однако из осведомлённости не следует познание: турбулентность — одна из наименее понятных областей физического мира.

Пример потока без турбулентности — это спокойная река. Каждая её часть движется в одном и том же направлении с одной и той же скоростью. Турбулентная жидкость появляется, когда поток реки ломается так, что разные части потока начинают двигаться в разных направлениях с разными скоростями. Физики описывают формирование турбулентности сперва как появление воронки в гладком потоке, а затем как формирование мелких воронок в первой воронке, и ещё более мелких воронок в этих воронках — море воронок, уходящих внутрь жидкости, так, что жидкость разбивается на дискретные части, каждая из которых взаимодействует друг с другом и движется в своём собственном направлении.

Исследователи хотят понять, как именно гладкий поток разбивается на турбулентные завихрения, и смоделировать будущую форму жидкости, после того, как турбулентность взяла своё. Но Задача тысячелетия формулируется более скромно: нужно лишь доказать, что решения всегда существуют. То есть, вопрос в том, могут ли уравнения описать любую жидкость, с любыми начальными условиями, и до бесконечно далёкого будущего?

«Первый шаг — просто попытаться доказать, что у уравнений есть какие-то решения, — говорит Чарли Фефферман, математик из Принстонского университета. — Это не даёт настоящего понимания поведения жидкостей, но если у вас и этого нет, то вы вообще ничего не знаете».

Так как можно доказать существование решений? Начать нужно с того, чтобы понять, из-за чего их может не оказаться. Уравнения Навье-Стокса подразумевают подсчёт изменения таких величин, как скорость и давление. Математиков беспокоит следующий вариант развития событий: вы прогоняете эти уравнения, и через какое-то конечное время они сообщают вам, что частица жидкости движется с бесконечной скоростью. А это проблема — подсчитать изменение бесконечного значения не проще, чем поделить на ноль. Математики называют такие ситуации «взрывом», и в случае взрыва уравнения перестают работать и решений не находится.

Уравнения Навье-Стокса описывают поток несжимаемой жидкости.

В целом произведение массы (голубая часть) на ускорение (фиолетовая) приравнивается к силам, действующим на жидкость (оранжевая):

• ρ — плотность жидкости;
• dV/dt — изменение скорости по времени;
• V ∇V — скорость и направление движения;
• ∇P — изменение внутреннего давления;
• ρ g — влияние внешних сил (к примеру, гравитации);
• μ ∇ 2 V — влияние внутренних сил (вязкость).

Доказательство отсутствия взрывов (и существования решений) равносильно доказательству того, что максимальная скорость любой частицы жидкости остаётся ограниченной неким конечным значением. Одной из наиболее важных величин оказывается кинетическая энергия жидкости.

Когда вы начинаете моделировать поток при помощи уравнений Навье-Стокса, у вашей жидкости есть некое начальное количество энергии. В турбулентных потоках энергия может начать концентрироваться. Вместо того, чтобы равномерно распространяться по всей реке, кинетическая энергия может собираться в водоворотах произвольно малого размера, и частицы в этих водоворотах (теоретически) могут разогнаться до бесконечной скорости.

«При переходе на всё меньшие и меньшие масштабы, кинетическая энергия становится всё менее и менее полезной для контроля решения. Решение может делать, что угодно, и я не буду знать, как его контролировать», — говорит Влад Викол, математик из Принстонского университета, написавший новую работу вместе с Тристаном Бакмастером.

Математики классифицируют частично дифференциальные уравнения на основании того, до какой степени они могут начать вести себя плохо на бесконечно малых масштабах. Уравнения Навье-Стокса находятся на экстремальном конце этой шкалы. Сложность математики уравнений в каком-то смысле отражает сложность турбулентных потоков, которые они должны уметь описывать.

«Когда вы увеличиваете масштаб в каком-то месте, то с математической точки зрения вы теряете информацию о решении, — говорит Викол. — Но турбулентность должна описывать именно это — передачу кинетической энергии от крупных ко всё более мелким масштабам, поэтому она прямо-таки просит вас увеличивать масштаб».

Говоря о математических свойствах физических уравнений, естественно задаться вопросом: а изменят ли эти рассуждения то, как мы расцениваем физический мир? В случае с уравнениями Навье-Стокса и Задачей тысячелетия ответ будет одновременно «да» и «нет». После почти 200 лет экспериментов ясно, что уравнения работают: течение, предсказанное Навье-Стоксом, последовательно совпадает с течением, наблюдаемым в экспериментах. Если вы — физик, работающий в лаборатории, вам этого может быть достаточно. Но математикам нужно знать больше — они хотят проверить, можно ли следовать этим уравнениям до упора, чтобы следить за тем, как именно меняется поток, от одного момента времени к другому (для любой начальной конфигурации жидкости), и даже уловить источник турбулентности.

«Поведение жидкостей таит в себе сюрпризы, — говорит Фефферман. — Эти сюрпризы в принципе объясняются фундаментальными уравнениями, управляющие потоками жидкостей, но как перейти от уравнений, управляющих движением жидкости, к описанию того, как на самом деле движется жидкость — это загадка».

Видео:Как решают уравнения в России и СШАСкачать

10 нерешенных математических задач, с которыми академики бьются и по сей день

Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать

Гипотеза Коллатца

Небольшой прогресс в решении этой задачи почти вековой давности наметился буквально в прошлом месяце. Однако знаменитый американской математик Терренс Тао лишь ближе всех подошел к нему, но ответа все равно пока не нашел. Гипотеза Коллатца является фундаментом такой математической дисциплины, как «Динамические системы», которая, в свою очередь, важна для множества других прикладных наук, например, химии и биологии. Сиракузская проблема выглядит, как простой безобидный вопрос, но именно это делает ее особенной. Несмотря на все попытки, эта проблема до сих пор остается самой известной нерешенной математической задачей.

Видео:Обманул балди и решил 3 пример😱Скачать

Проблема Гольдбаха (бинарная)

Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: «каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этого варианта. Однако предложенное Эйлером следствие этого утверждения, которое и назвали «бинарной проблемой Гольдбаха», до сих пор не поддается никому. Это одна из самых древних нерешенных математических задач человечества.

Видео:Мэри решает сложные примеры по математике | Одарённая (2017)Скачать

Гипотеза о числах-близнецах

Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии. Однако, до сих пор она остается нерешенной математической проблемой, над которой бьются лучшие умы.

Видео:Прогульщик опоздал на 20-мин. и получил две ЗАДАЧИ... Его ответ поставил профессора в ступор...Скачать

Гипотеза Римана

Одна из «проблем тысячелетия», за решение которой назначен приз в миллион долларов, а также вхождение в пантеон «богов» современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что «гипотеза Римана» верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако до сих пор она остается, пожалуй, самой неприступной нерешенной задачей современной математики.

Видео:Математика это не ИсламСкачать

Гипотеза Берча и Суиннертон-Дайера

Эллиптическими кривыми называются такие линии на графике, которые описываются, на первый взгляд, безобидными уравнениями вида y²=x³+ax+b. Некоторые их свойства чрезвычайно важны для алгебры и теории чисел, а решение данной задачи может серьезно продвинуть науку вперед. Наибольший прогресс в нахождении ответа на эту нерешенную математическую задачу был достигнут в 1977 году коллективом математиков из Англии и США, которые смогли найти доказательство гипотезы Берча и Суиннертон-Дайера для одного из частных случаев.

Видео:Как выглядит самая сложная задача математики? Фрактал КоллатцаСкачать

Проблема плотной упаковки равных сфер

Под размерностью или измерением понимается количество линий, вдоль которых размещаются шары. В реальной жизни больше третьей размерности не встречается, однако математика оперирует и гипотетическими значениями. Решение этой задачи может серьезно продвинуть не только теорию чисел и геометрию вперед, но также поможет в химии, информатике и физике. Пожалуй, это одна из немногих нерешенных математических задач, которая имеет четкое практическое применение.

Видео:9 Математических Загадок, Которые Поставят в Тупик Даже Самых УмныхСкачать

Проблема развязывания

Первые шаги на пути решения этой задачи были сделаны в 2011 году американским математиком Грегом Купербергом. В его работе развязывание узла из 139 вершин было сокращено со 108 часов до 10 минут. Результат впечатляющий, но это лишь частный случай. На данный момент существует несколько десятков алгоритмов разной степени эффективности, однако ни один из них не является универсальным. Среди применений этой области математики — биология, в частности, процессы сворачивания белков.

Видео:ЖЕСТКАЯ задача на логику! Попробуй решить!Скачать

Самый большой кардинал

Мощность множества характеризуется его кардинальным числом или просто кардиналом. Существует целая онлайн-энциклопедия бесконечностей и примечательных «конечностей», названная в честь Георга Кантора. Этот немецкий математик первым обнаружил, что неисчислимые множества могут быть больше или меньше друг друга. Более того, он смог доказать разницу в мощностях различных бесконечностей. Проблема тут заключается в доказательстве того, что существует кардинал (или, возможно, кардиналы) с некоторым заданным большим кардинальным свойством. До сих пор эта задача остается нерешенной.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Что не так с суммой числа π и e?

Если от предыдущего абзаца у читателя не заболела голова, то вот продолжение загадки — а что с πe, π/e и π-e? Также неизвестно, а знать это наверняка довольно важно для теории чисел. Трансцедентность числа доказал в конце XIX века Фердинанд фон Линдеман вместе с невозможностью решения задачи квадратуры круга. С тех пор значимых подвижек в решении вопроса не было.

Видео:Переставь одну цифру! Задача на логикуСкачать

Является ли γ рациональной?

Значение γ было вычислено до нескольких тысяч знаков после запятой, первые четыре из которых — 0,5772. Она достаточно широко используется в математике, в том числе вместе с другим числом Эйлера — e. Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени. Но пока доказать ее рациональность не удалось — для этого нам и нашим компьютерам нужно больше времени. До этих пор рациональность постоянной γ остается нерешенной математической проблемой.

Кстати, мы недавно запустили ютуб-канал! В новом видео рассказали о главных достижениях женщин-ученых, о которых все почему-то забыли:

💡 Видео

Решаем два варианта Добротина за 2 часаСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Думала не справлюсь😂 #shortsСкачать

8 ЛОГИЧЕСКИХ ЗАГАДОК ДЛЯ САМЫХ УМНЫХ! Насколько хорошо развит твой мозг?Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать