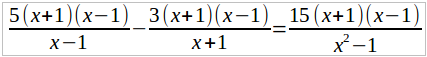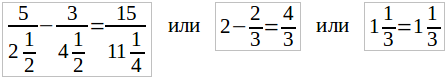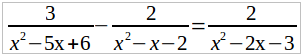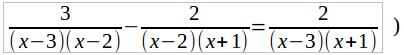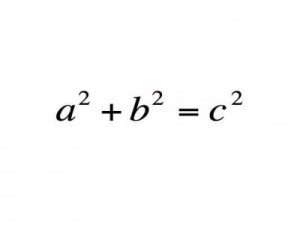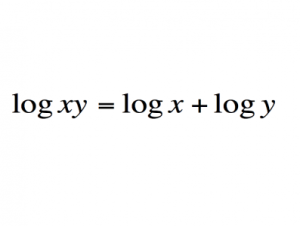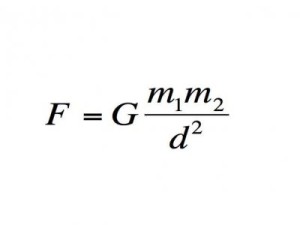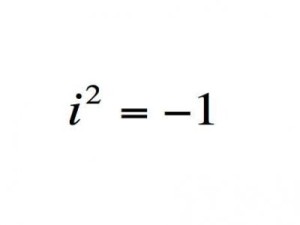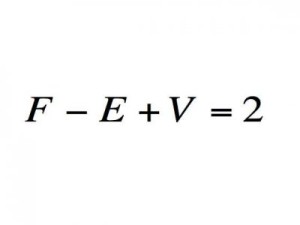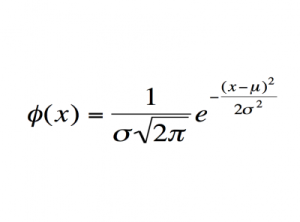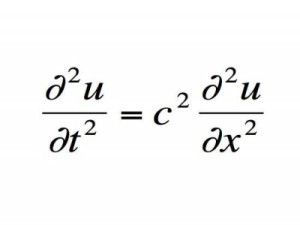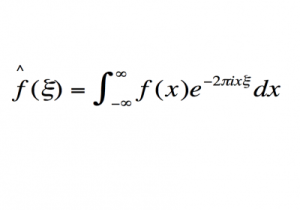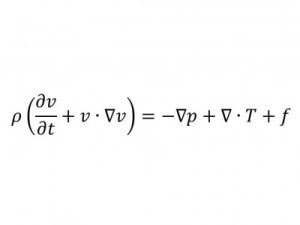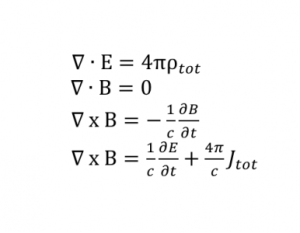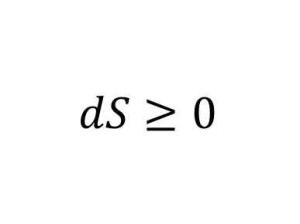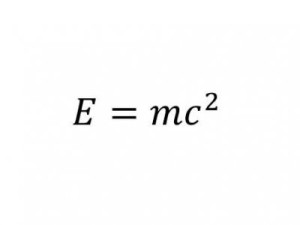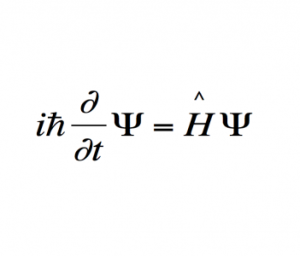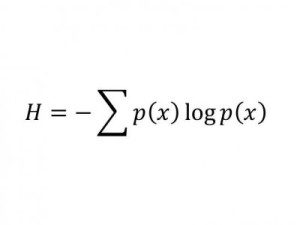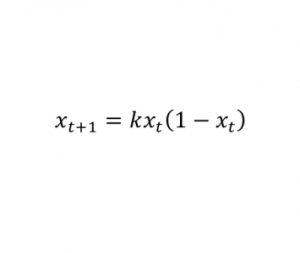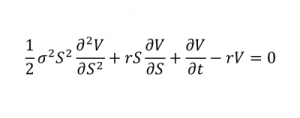Самое сложное уравнение в мире алгебра (2 видео)

Математические уравнения, которые изменили мир

Для большинства людей математика — это что-то скучное и совершенно ненужное в обычной жизни. Глядя на все эти цифры, сложно понять, что в них такого. На самом деле математика, наравне с физикой — самые важные предметы, ведь она по сути раскрывает секреты мироздания.

В этой статье мы расскажем о математических уравнениях, которые изменили мир. И, может быть, в очередной раз взглянув на эти цифры, ты уже будешь думать о них не просто как о наборе символов, а как о чем-то, что помогло человечеству продвинуться вперед.

Содержание

Теорема Пифагора
Закон всемирного тяготения Ньютона
Логарифмы
Второй закон термодинамики
Преобразование Фурье
Концепция эквивалентности массы и энергии
Уравнения Максвелла
Уравнение Шредингера
Математика
Формулы и уравнения, которые изменили мир
Теорема Пифагора
Логарифм и его тождество
Основная теорема анализа
Классическая теория тяготения Ньютона
Комплексные числа
Эйлерова характеристика полиэдров
Нормальное распределение
Волновое уравнение
Преобразование Фурье
Уравнения Навье—Стокса
Уравнения Максвелла
Второй закон термодинамики
Теория относительности Эйнштейна
Уравнение Шрёдингера
Информационная энтропия Шаннона
Логистическая модель роста популяций
Модель Блэка-Скоулза
Вместо заключения
📽️ Видео

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Теорема Пифагора

Вряд ли кто-то не слышал или не видел этой теоремы, даже если он плохо учился в школе. Она говорит о том, что сумма квадратов длин катетов равна квадрату гипотенузы. Если говорить простыми словами, то это отношение длин сторон прямоугольного треугольника.

Казалось бы, одна из самых простых формул, глядя на которую, глаза не начинают слезиться от огромного количества символов, но она сделала для человечества очень много. Помимо архитектуры и других инженерных дисциплин, теорема Пифагора применяется в навигации, картографии и других важных для человечества науках.

Теорему Пифагора применяют в таком большом количестве точных наук, что проще сказать, где она не используется. Несмотря на то, что теорема была открыта несколько тысячелетий назад, она до сих пор служит на благо человечества.

Видео:Как выглядит самая сложная задача математики? Фрактал КоллатцаСкачать

Закон всемирного тяготения Ньютона

Эта формула выглядит чуть сложнее, чем предыдущая, и она принесла не меньше благ человечеству. Исаак Ньютон, одна из самых выдающихся личностей в науке, открыл этот закон около 1666 года и буквально перевернул им мир.

Эта формула позволила лучше понять движение различных физических объектов и явлений. Причем Ньютон своим законом заложил основы для более сложных научных теорий, таких как Общая теория относительности и Квантовая гравитация.

Видео:Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать

Логарифмы

Пожалуй, самые нелюбимые формулы у школьников, ведь мало кто понимает их суть и необходимость. Может сейчас важность логарифмов и не так велика, но в прошлом, до появления цифровых компьютеров, они являлись наиболее быстрым способом умножения больших чисел.

Ну, и что такого, спросишь ты, умножать стали быстрее, как же это повлияло на мир? А так, что теперь ученые смогли сосредоточиться на воплощении своих теорий в жизнь, а не на долгих и нудных подсчетах.

Видео:19 задание: Теория чисел | Математика с Кириллом Нэш | ЕГЭ 2024 | SMITUPСкачать

Второй закон термодинамики

Второй закон термодинамики говорит о том, что в закрытой системе энтропия всегда постоянна и возрастает. Звучит непонятно, если не разобраться. Если сказать просто, то в системе, которая первоначально находится в упорядоченном неравномерном состоянии, например, горячая рядом с холодной, они будут стремиться к выравниванию, то есть к стабилизации температур, пока они не станут одинаковыми. Кроме того, уравнение говорит, что каждый раз, когда энергия изменяется или перемещается, она становится менее полезной.

Казалось бы, и что здесь такого, и чем это поменяло мир? А тем, что благодаря этому закону началось развитие двигателей внутреннего сгорания, современной металлургии, эффективного производства электроэнергии и других сфер деятельности.

Видео:Сложное уравнение с дробями. Алгебра 7 класс.Скачать

Преобразование Фурье

Французский математик Жан-Батист Жозеф Фурье сформулировал свое уравнение интегралов еще в начале 19 века, но они до сих пор используются в науке. Если говорить простым языком, то преобразования Фурье необходимы для понимания более сложных волновых структур, например, человеческой речи, позволяя разбить беспорядочную функцию на комбинацию простых волн. Это значительно упрощает анализ сигналов.

Для каких сфер она несет пользу? Для астрономии, акустики, радиотехники и для других, работающих со звуком. Ты сталкиваешься с преобразованием Фурье каждый раз, когда слушаешь музыку или голосовое сообщение, включаешь радио в машине и так далее.

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Концепция эквивалентности массы и энергии

Думаем, ты слышал об уравнении Альберта Эйнштейна, сформулированном им в 1905 году, хотя на самом деле оно было предложено еще до знаменитого ученого. Казалось бы, что в нем особенного, ведь оно куда короче всего того, что преподают на математике даже на гуманитарных факультетах. Но с этой концепцией человечество вступило в новую эпоху.

Опираясь на эту формулу, ученые изучают космос, строят ускорители частиц, стараются понять природу субатомного мира. Концепция стала настолько известной, что, наравне со значком атома, является одним из главных символов науки.

Видео:Математика это не ИсламСкачать

Уравнения Максвелла

Британский физик, математик и механик Джеймс Клерк Максвелл был весьма плодовит в плане науки и заложил основы современной классической электродинамики, а также ввел несколько понятий в физику, которые используются и по сей день.

Одним из главных трудов Максвелла стала система из 20 уравнений, описывающих работу электрических и магнитных полей, а также их взаимодействие. В настоящее время уравнения Максвелла представляют собой систему из четырех уравнений, которые можно описать следующими словами:

1. Электрический заряд является источником электрической индукции.
2. Магнитные заряды не обнаружены.
3. Изменение магнитной индукции порождает вихревое электрическое поле.
4. Электрический ток и изменение электрической индукции порождают вихревое магнитное поле.

Выглядит как китайская грамота для гуманитарных умов, но поверь, без этих четырех уравнений ты бы, возможно, не пользовался сейчас благами цивилизации вроде компьютеров, смартфонов и другой техники, работающей на электричестве, или, как минимум, они выглядели бы иначе.

Видео:Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

Уравнение Шредингера

Многие знают ученого Эрвина Шредингера только по мысленному эксперименту «кота Шредингера». Но этот австрийский ученый сделал для науки куда больше, чем простой мысленный эксперимент, выведя уравнение, описывающее, как состояние квантовой системы изменяется со временем и определяет поведение атомов и субатомных частиц в квантовой механике.

Эта сложная формула открыла человечеству путь к атомной энергетике, микрочипам, квантовым вычислениям и другим важным для современного общества дисциплинам.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Математика

52. Более сложные примеры уравнений.
Пример 1 .

5/(x – 1) – 3/(x + 1) = 15/(x 2 – 1)

Общий знаменатель есть x 2 – 1, так как x 2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x 2 – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

5x + 5 – 3x + 3 = 15

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x 2 – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

2x 2 + 6x – 2x – 6 = 2x 2 + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x 2 . Однако, мы можем от обеих частей уравнения вычесть по 2x 2 — от этого уравнение не нарушится; тогда члены с x 2 уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

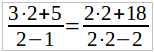
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x 2 + 4x – 10 = 2x 2 + 16x – 18.

Здесь уже члены с x 2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2 2 – 3 · 2 = –2 и 2) 1 2 – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x 2 – 5x + 6 = x 2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x 2 – x – 2 = x 2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x 2 – 2x – 3 = x 2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

3x + 3 – 2x + 6 = x – 2

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Видео:Уравнение годаСкачать

Формулы и уравнения, которые изменили мир

Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен и приводит примеры их практического применения.

Теорема Пифагора

Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Важность: Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.

Современное использование: Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.

Логарифм и его тождество

Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.

Важность: Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.

Современное использование: Логарифмы важная составляющая для понимания радиоактивного распада.

Основная теорема анализа

Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Важность: Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.

Современное использование: Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.

Классическая теория тяготения Ньютона

Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.

Важность: Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом. Мы используем ее и по сей день для проектирования орбит спутников и космических аппаратов.

Современное использование: Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.

Комплексные числа

Комплексные числа — расширение поля вещественных чисел.

Важность: Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.

Современное использование: Широко используется в электротехнике и сложных математических теориях.

Эйлерова характеристика полиэдров

Важность: Внесла вклад в понимание топологического пространства, в котором рассматриваются только свойства непрерывности. Необходимый инструмент для инженеров и биологов.

Современное использование: Топология используется, чтобы понять поведение и функции ДНК.

Нормальное распределение

Важность: Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.

Современное использование: Используется в клинических испытаниях для определения эффективности лекарств по сравнению с отрицательными побочными эффектами.

Волновое уравнение

Дифференциальное уравнение, описывающее поведение волн.

Важность: Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.

Современное использование: Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.

Преобразование Фурье

Важность: Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.

Современное использование: Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.

Уравнения Навье—Стокса

В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.

Важность: Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.

Современное использование: Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.

Уравнения Максвелла

Описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Важность: Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.

Современное использование: Радар, телевидение и современные средства связи.

Второй закон термодинамики

Вся энергия и тепло со временем исчезнет.

Важность: Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.

Современное использование: Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.

Теория относительности Эйнштейна

Энергия равна массе, умноженной на квадрат скорости света.

Важность: Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.

Современное использование: Помогло создать ядерное оружие. Используется в GPS навигации.

Уравнение Шрёдингера

Нелинейное уравнение Шрёдингера

Описывает материю как волну, а не как частицу.

Важность: Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.

Современное использование: Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.

Информационная энтропия Шаннона

Оценивает количество данных в куске кода путем расчета вероятности его символов.

Важность: Это уравнение, которое открыло дверь в Информационную Эпоху.

Современное использование: В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).

Логистическая модель роста популяций

Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.

Важность: Помогла в развитии теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.

Современное использование: Используется для моделирования землетрясений и прогноза погоды.

Модель Блэка-Скоулза

Модель Блэка Скоулза

Одна из моделей ценообразования опционов.

Важность: Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.

Современное использование: Даже после кризиса используются для определения цен.

Вместо заключения

В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина—Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. Мы надеемся, что нам удалось показать насколько важна математика, и насколько бесценен ее вклад для всех людей.