Сегодня мы снова настроены на математическую тематику. Ведь в руки нам попал задачник СССР с математическими олимпиадными заданиями. В этом задачнике есть различные примеры, есть и такая категория примеров, которые вообще не имеют решения. Давайте посмотрим первый пример…
Он довольно простой. Почему этот пример не имеет решения?
Итак, первый пример… Разберем подробно…
- 7+1 = 8
- 7+1-8 = 0
- 1+7+7-1 = 14
- 14/0 — на ноль делить нельзя. Пример не имеет решение
Раскрываем скобки. Для этого значение перед скобками, умножаем на каждое значение в скобках, и складываем их в соответствии с их знаками. Тогда получаем:
- Решение простых линейных уравнений
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- Нерешаемые задачи: уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия
- Предыстория
- Институт Клэйя
- Задачи тысячелетия
- Что доказал Григорий Перельман
- Теория Янга-Миллса
- Уравнения Навье-Стокса
- Задача Берча — Свиннертон-Дайера
- Равенство классов p и np
- Гипотеза Римана
- Гипотеза о циклах Ходжа
- 💡 Видео
Видео:Ученые не могут решить простую математическую задачу уже больше 80 летСкачать

Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать
![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg)
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Видео:Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать
![Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]](https://i.ytimg.com/vi/QgzBDZwanWA/0.jpg)
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
- Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Видео:Переставь одну цифру! Задача на логикуСкачать

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
- Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
- Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
Видео:Уравнение, которое может решить только 2 школьниковСкачать

Нерешаемые задачи: уравнения Навье-Стокса, гипотеза Ходжа, гипотеза Римана. Задачи тысячелетия
Нерешаемые задачи — это 7 интереснейших математических проблем. Каждая из них была предложена в свое время известными учеными, как правило, в виде гипотез. Вот уже много десятилетий над их решением ломают головы математики во всем мире. Тех, кто добьется успеха, ждет вознаграждение в миллион американских долларов, предложенное институтом Клэйя.
Видео:Задача, которую на моей памяти не решил ещё никтоСкачать

Предыстория
В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.
Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:
- проблема непротиворечивости арифметических аксиом;
- общий закон взаимности на пространстве любого числового поля;
- математическое исследование физических аксиом;
- исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
- проблема строгого обоснования исчислительной геометрии Федора Шуберта;
- и пр.
Видео:ЖЕСТКАЯ задача на логику! Попробуй решить!Скачать

Институт Клэйя
Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.
В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Задачи тысячелетия
В список института Клэйя изначально входили:
- гипотеза о циклах Ходжа;
- уравнения квантовой теории Янга — Миллса;
- гипотеза Пуанкаре;
- проблема равенства классов Р и NP;
- гипотеза Римана;
- уравнения Навье Стокса, о существовании и гладкости его решений;
- проблема Берча — Свиннертон-Дайера.
Эти открытые математические проблемы представляют огромный интерес, так как могут иметь множество практических реализаций.
Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Что доказал Григорий Перельман
В 1900 году известный ученый-философ Анри Пуанкаре предположил, что всякое односвязное компактное 3-мерное многообразие без края гомеоморфно 3-мерной сфере. Ее доказательство в общем случае не находилось в течение века. Лишь в 2002-2003 годах петербургский математик Г. Перельман опубликовал ряд статей с решением проблемы Пуанкаре. Они произвели эффект разорвавшейся бомбы. В 2010 году гипотеза Пуанкаре была исключена из списка «Нерешенные задачи» института Клэйя, а самому Перельману было предложено получить полагающееся ему немалое вознаграждение, от которого последний отказался, не объяснив причин своего решения.
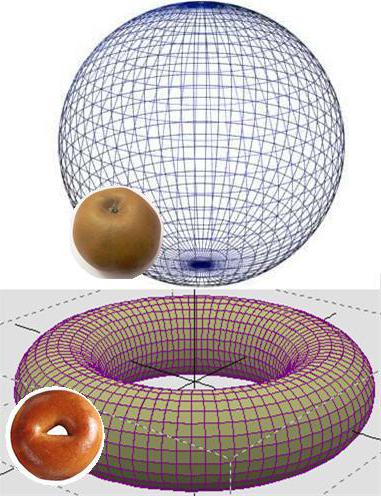
Самое понятное объяснение того, что удалось доказать российскому математику, можно дать, представив, что на бублик (тор), натягивают резиновый диск, а затем пытаются стянуть края его окружности в одну точку. Очевидно, что это невозможно. Другое дело, если произвести этот эксперимент с шаром. В таком случае вроде бы трехмерная сфера, получившаяся из диска, окружность которого стянули в точку гипотетическим шнуром, будет трехмерной в понимании обычного человека, но двумерной с точки зрения математики.
Пуанкаре предположил, что трехмерная сфера является единственным трехмерным «предметом», поверхность которой можно стянуть в одну точку, а Перельману удалось это доказать. Таким образом, список «Нерешаемые задачи» сегодня состоит из 6 проблем.
Видео:Показательные и логарифмические уравнения | Подготовка к ЕГЭ по математике 2024Скачать

Теория Янга-Миллса
Эта математическая проблема была предложена ее авторами в 1954-м году. Научная формулировка теории имеет следующий вид: для любой простой компактной калибровочной группы квантовая пространственная теория, созданная Янгом и Милльсом, существует, и при этом имеет нулевой дефект массы.
Если говорить на языке, понятном для обычного человека, взаимодействия между природными объектами (частицами, телами, волнами и пр.) делятся на 4 типа: электромагнитное, гравитационное, слабое и сильное. Уже много лет физики пытаются создать общую теорию поля. Она должна стать инструментом для объяснения всех этих взаимодействий. Теория Янга-Миллса — это математический язык, с помощью которого стало возможно описать 3 из 4-х основных сил природы. Она не применима к гравитации. Поэтому нельзя считать, что Янгу и Миллсу удалось создать теорию поля.
Кроме того, нелинейность предложенных уравнений делает их крайне сложными для решения. При малых константах связи их удается приближенно решить в виде ряда теории возмущений. Однако пока непонятно, как можно решить эти уравнения при сильной связи.
Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Уравнения Навье-Стокса
С помощью этих выражений описываются такие процессы, как воздушные потоки, течение жидкостей и турбулентность. Для некоторых частных случаев аналитические решения уравнения Навье-Стокса уже были найдены, однако сделать это для общего пока никому не удалось. В то же время, численное моделирование для конкретных значений скорости, плотности, давления, времени и так далее позволяет добиться прекрасных результатов. Остается надеяться, что у кого-нибудь получится применить уравнения Навье-Стокса в обратном направлении, т. е. вычислить с их помощью параметры, либо доказать, что метода решения нет.
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Задача Берча — Свиннертон-Дайера
К категории «Нерешенные задачи» относится и гипотеза, предложенная английскими учеными из Кембриджского университета. Еще 2300 лет назад древнегреческий ученый Эвклид дал полное описание решений уравнения x2 + y2 = z2.
Если для каждого из простых чисел посчитать количество точек на кривой по его модулю, получится бесконечный набор целых чисел. Если конкретным образом «склеить» его в 1 функцию комплексной переменной, тогда получится дзета-функция Хассе-Вейля для кривой третьего порядка, обозначаемая буквой L. Она содержит информацию о поведении по модулю всех простых чисел сразу.
Брайан Берч и Питер Свиннертон-Дайер выдвинули гипотезу относительно эллиптических кривых. Согласно ей, структура и количество множества ее рациональных решений связаны с поведением L-функции в единице. Недоказанная на данный момент гипотеза Берча — Свиннертон-Дайера зависит от описания алгебраических уравнений 3 степени и является единственным сравнительно простым общим способом расчета ранга эллиптических кривых.
Чтобы понять практическую важность этой задачи, достаточно сказать, что в современной криптографии на эллиптических кривых основан целый класс асимметричных систем, и на их применении основаны отечественные стандарты цифровой подписи.
Видео:✓ Простое решение задачи из Кембриджа | В интернете кто-то неправ #029 | Пётр Земсков и Борис ТрушинСкачать

Равенство классов p и np
Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Гипотеза Римана
Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных. Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.
Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.
Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.
Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др. Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.
Видео:Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Гипотеза о циклах Ходжа
Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.
Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.
💡 Видео
Этому больше не учат! Советская задача, которую не могут решить нынешние школьники.Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

🤯 САМОЕ ПРОСТОЕ неравенство #shortsСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать