С помощью какого уравнения регрессии исследуется линейная связь между факторами

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Видео:Парная регрессия: линейная зависимостьСкачать

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Видео:Эконометрика. Линейная парная регрессияСкачать

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Видео:Множественная линейная регрессия, часть 1Скачать

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Видео:Множественная регрессия в ExcelСкачать

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Видео:Математика #1 | Корреляция и регрессияСкачать

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ STATISTICA #12Скачать

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Видео:Парный линейный регрессионный анализСкачать

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Видео:РЕГРЕССИОННЫЙ АНАЛИЗ этапы | АНАЛИЗ ДАННЫХ #17Скачать

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Видео:Коэффициент корреляции. Статистическая значимостьСкачать

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Видео:Метод наименьших квадратов. Регрессионный анализ.Скачать

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Видео:Расчет коэффициента корреляции в ExcelСкачать

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Видео:Лекция 8. Линейная регрессияСкачать

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Видео:Линейные модели 2023 | Линейная регрессияСкачать

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Видео:Множественная регрессияСкачать

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Видео:Эконометрика. Построение модели множественной регрессии в Excel.Скачать

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.

Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Основы линейной регрессии

Видео:КОРРЕЛЯЦИЯ Спирмена Пирсона Кенделла | АНАЛИЗ ДАННЫХ #12Скачать

Что такое регрессия?

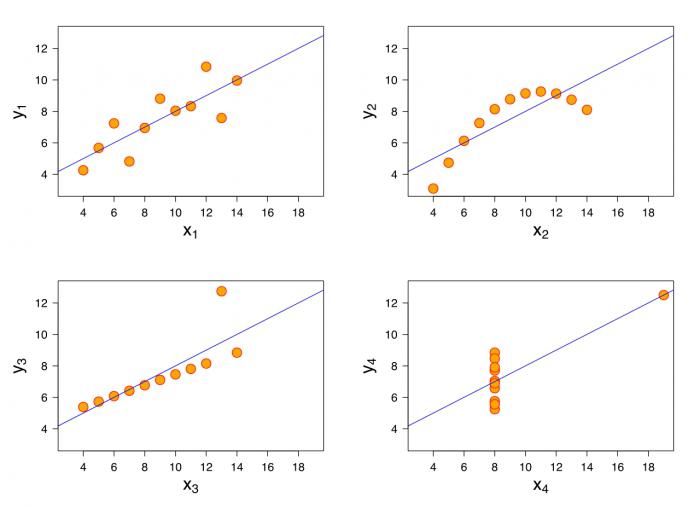
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Видео:Тема 6 Регрессионный анализСкачать

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Видео:Корреляционно регрессионный анализ примерСкачать

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

• Остатки нормально распределены с нулевым средним значением;

• Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

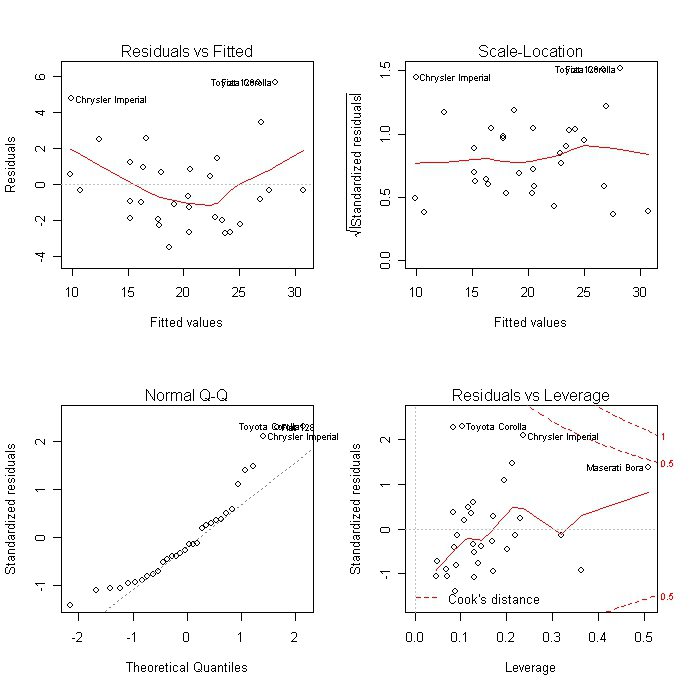
Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

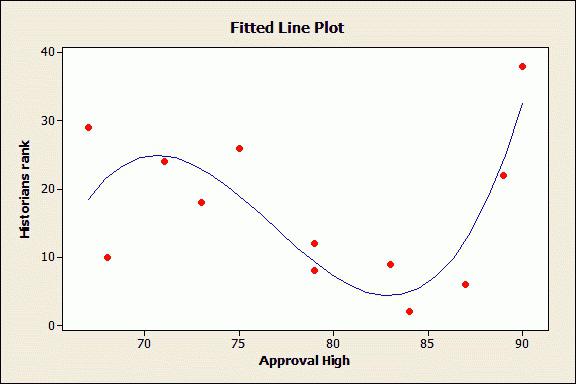
Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Линейная регрессия в машинном обучении

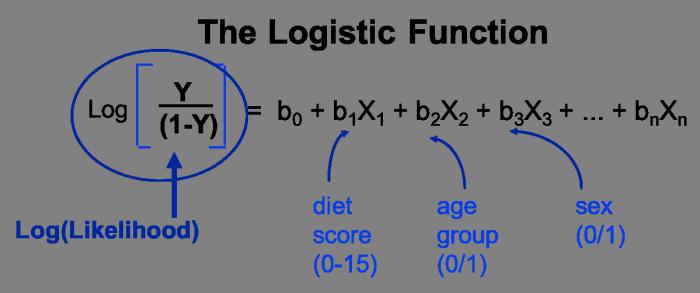
Линейная регрессия ( Linear regression ) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.

Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала прос тым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.

Применение линейной регрессии

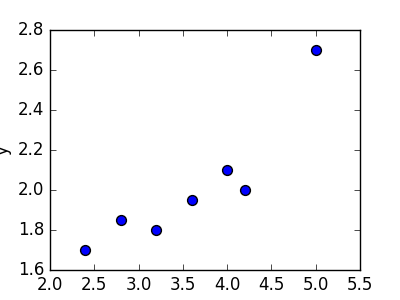
Предположим, нам задан набор из 7 точек (таблица ниже).

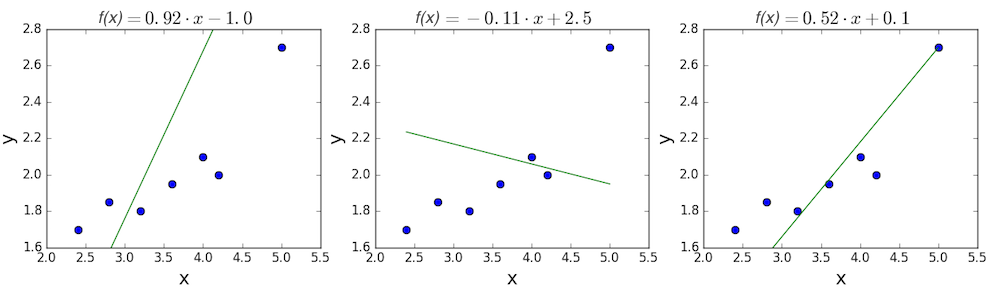
Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:

Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.

Функция потерь — метод наименьших квадратов

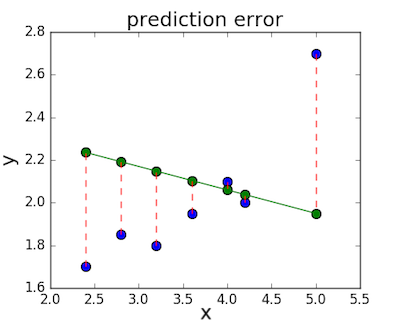
Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y( х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.

Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.

Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.

Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.

Слева: диаграмма, изображающая среднеквадратичную ошибку для -2≤m≤4, -6≤p≤8 Справа: тот же рисунок, но визуализирован как контурный график, где контурные линии являются логарифмически распределенными поперечными сечениями высоты.

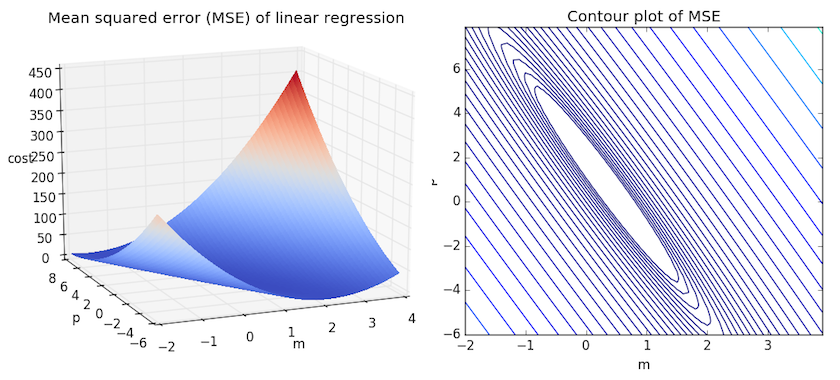
Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Есл и мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.

Больше размерностей

Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:

Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:

Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.

Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.

Проклятие нелинейности

Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.

Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).

Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.

Минимум функции

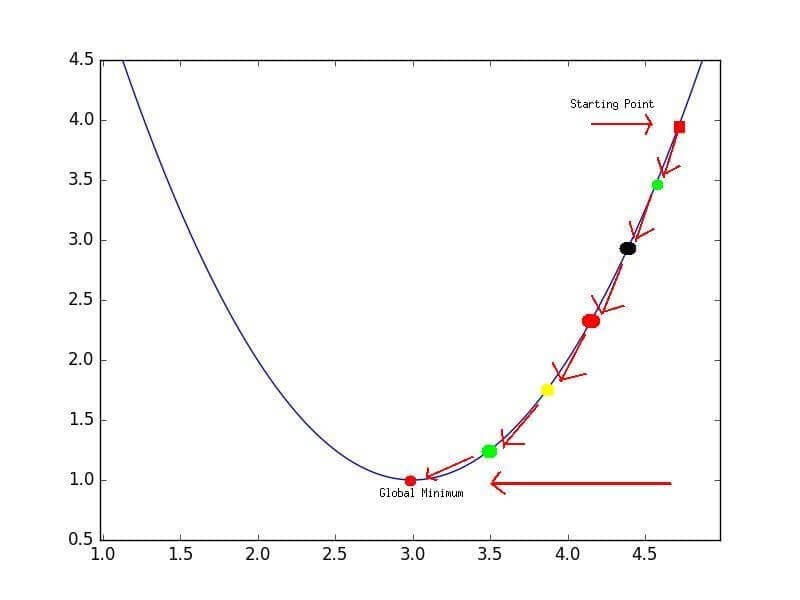
Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.