С помощью графика функции y cos x найти корни уравнения принадлежащие данному промежутку cos x (4 видео)

С помощью графика функции y = cos(x) найти корни уравнения

Формулировка задания: С помощью графика функции y = cos(x) найти корни уравнения cos(x) = √2/2 на отрезке [-3π/2; 0].

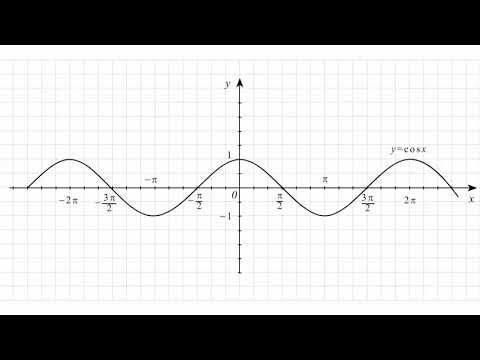
Построим график функции y = cos(x):

Определим границы отрезка, на котором нужно найти корни уравнения:

Проведем прямую y = √2/2 (≈ 1,4/2 = 0,7) на этом же графике:

И найдем точки пересечения графиков:

Такая точка лишь одна, следовательно, уравнение имеет один корень x = –π/4.

Поделитесь статьей с одноклассниками «С помощью графика функции y = cos(x) найти корни уравнения – решение и ответ».

Содержание

Функция y = cos x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
п.2. Свойства функции y=cosx⁡
п.3. Примеры
Презентация к уроку алгебры по теме « y=cos x@
Описание презентации по отдельным слайдам:
Краткое описание документа:
💡 Видео

Видео:Построение графика функции y = cos xСкачать

Функция y = cos x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x косинусоидой .
Часть косинусоиды для –π≤x≤π называют волной косинусоиды .
Часть косинусоиды для (-fracpi2leq xleqfracpi2) называют полуволной или аркой косинусоиды .

Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».

п.2. Свойства функции y=cosx⁡

1. Область определения (xinmathbb) — множество действительных чисел.

2. Функция ограничена сверху и снизу $$ -1leq cosxleq 1 $$ Область значений (yin[-1;1])

3. Функция чётная $$ cos(-x)=cosx $$

4. Функция периодическая с периодом 2π $$ cos(x+2pi k)=cosx $$

5. Максимальные значения (y_=1) достигаются в точках $$ x=2pi k $$ Минимальные значения (y_=-1) достигаются в точках $$ x=pi+2pi k $$ Нули функции (y_=cosx_0=0) достигаются в точках (x=fracpi2 +pi k)

6. Функция возрастает на отрезках $$ -pi+2pi kleq xleq 2pi k $$ Функция убывает на отрезках $$ 2pi kleq xleqpi+2pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:

a) (left[fracpi6; fracright]) $$ y_=cosleft(fracright)=-frac<sqrt>, y_=cosleft(fracpi6right)=frac<sqrt> $$ б) (left[frac; fracright]) $$ y_=cos(pi)=-1, y_=cosleft(fracright)=frac12 $$

Пример 2. Решите уравнение графически:
a) (cosx=fracpi2-x)

Один корень: (x=fracpi2)

б) (cosx-x=1)
(cosx=x+1)

Один корень: x = 0

в) (cosx-x^2=1)
(cosx=x^2+1)

Один корень: x = 0

г*) (cosx-x^2+frac=0)
(cosx=x^2-frac)
(y=x^2-frac) – парабола ветками вверх, с осью симметрии (x_0=0) (ось OY) и вершиной (left(0; -fracright)) (см. §29 справочника для 8 класса)

Два корня: (x_=pmfracpi2)

Пример 3. Постройте в одной системе координат графики функций $$ y=cosx, y=-cosx, y=2cosx, y=cosx-2 $$

(y=-cosx) – отражение исходной функции (y=cosx) относительно оси OX. Область значений (yin[-1;1]).
(y=2cosx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=cosx-2) — исходная функция опускается вниз на 2. Область значений (yin[-3;-1]).

Пример 4. Постройте в одной системе координат графики функций $$ y=cosx, y=cos2x, y=cosfrac $$

Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под косинусом изменяет период колебаний.
(y=cosx) – главная арка косинуса соответствует отрезку (-fracpi2leq xleqfracpi2)
(y=cos2x) — период уменьшается в 2 раза, главная арка укладывается в отрезок (-fracpi4leq xleqfracpi4).
(y=cosfrac) — период увеличивается в 2 раза, главная арка растягивается в отрезок (-pi leq xleq pi).

Видео:10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

Презентация к уроку алгебры по теме « y=cos x@

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 2 500 дидактических материалов для школьного и домашнего обучения

Столичный центр образовательных технологий г. Москва

Получите квалификацию учитель математики за 2 месяца

от 3 170 руб. 1900 руб.

Количество часов 300 ч. / 600 ч.

Успеть записаться со скидкой

Форма обучения дистанционная

311 лекций для учителей,
воспитателей и психологов

Получите свидетельство
о просмотре прямо сейчас!

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Функция определена на всей числовой прямой; Множество значений функции – отрезок [- 1; 1]

cos(x + 2π) = cos x, Функция y=cos x -периодическая с периодом 2π ( строим график на промежутке длиной 2π , например [- π; π])

o y x x Р (0;1) -1 cos x cos x 1 x на рис. видно, что функция y= cos x убывает на отрезке [0; π]

III II I IY p — шесть клеток Ось косинусов II Построение графика функции y = cosx с применением тригонометрического круга

1.Область определения – множество R всех действительных чисел y x График расположен вдоль всей оси OX

2. Множество значений функции 1 -1 График ограничен линиями У=-1 и У=1

3.Функция у= cos x периодическая с периодом 2π

4.Функция y= cos x – четная

5. У=0 при х= π/2 + πп, пє Z Наибольшее значение у=1, если х= 2 πп, пє Z Наименьшее значение у=-1, если х= Наибольшее значение у=1, если х= π+2 πп, пє Z У>0 на интервале (-π/2 ; π/2 ) и на интервалах со сдвигом на 2 πп У — ½, принадлежащие отрезку [-. » onclick=»aa_changeSlideByIndex(18, 0, true)» >

Пример 2: Найти все решения неравенства cos x > — ½, принадлежащие отрезку [- π; 2π] Решение: Из рисунка видно, что график функции y=cos x лежит выше графика функции у=-1/2 на промежутках (- 2π/3; 2π/3) и (4π/3; 2π) Ответ : — 2π/3 cos 8π/9 2) cos 8π/7 и cos 10π/7 Ответ: на интервале ( π; 2π ) функция возрастает, значит т.к. 8π/7 -9π/7, то cos(- 8π/7) cos 3 6) cos 4 и cos 5 Ответ: на интервале ( π; 2π) функция возрастает, значит т.к. 4 cos 3π/10, а значит cos π/5 > sin π/5 Ответ : cos π/5 > sin π/5 2) sin π/7 и cos π/7 Решение: sin π/7= sin (π/2 — π/7)= cos 5π/14. Сравним cos π/7 и cos 5π/14; π/7 cos 5π/14, а значит cos π/7 > sin π/7 Ответ : sin π/7

№ 714 Выразите синус через косинус по формулам приведения , сравните числа: 3) cos 3π/8 и sin 5π/8 Решение: sin 5π/8= sin (π/2 + π/8)= cos π/8. Сравним cos 3π/8 и cos π/8; π/8 π/10, значит cos 3π/5 π/7, значит cos π/6 cos π/5, а значит cos π/8 > sin 3π/10 Ответ : cos π/8 > sin 3π/10

№ 715 Найти все корни уравнения, принадлежащие отрезку [ -π/2; 3π/2] : 1) cos 2x= ½ Решение: На отрезке [ -π/2; 3π/2] корнем уравнения cos 2x = 1/2 является число 2х=arccos (1/2) = π/3. Решая уравнение 2х = π/3, получим х = π/6 Ответ : х = π/6

№ 715 Найти все корни уравнения, принадлежащие отрезку [ -π/2; 3π/2] : 2) cos 3x= /2 Решение: На отрезке [ -π/2; 3π/2] корнем уравнения cos 3x = /2 является число 3х=arccos ( /2) = π/6. Решая уравнение 3х = π/6, получим х = π/18 Ответ : х = π/18

№ 716 Найти все решения неравенства , принадлежащие отрезку [ -π/2; 3π/2] : 1) cos 2x /2 Решение: На отрезке [ -π/2; 3π/2] корнем уравнения cos 3x = /2 является число 3х=arccos ( /2) = π/6. Решая неравенство 0

Краткое описание документа:

Данный материал предназначен для учителей , работающих в 10 классе , а также для учащихся, пропустивших урок по данной теме. Презентация выполнена в полном соответствии с учебником. Данная презентация поможет учителю при повторении и при подготовке учащихся к итоговой аттестации. Используя решенные задания как образец, можно решать более сложные задачи. Кроме того, данная презентация может быть использована как материал для устного счета при изучении последующих тем: решение тригонометрических уравнений и неравенств, преобразование графиков функций.

Видео:Построение графика функции y=2cos(x)+1Скачать

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

Корни уравненияcosx=a.

2.Частые случаи решения уравнения sin x = a.

Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)