С помощью графика функции выяснить сколько корней имеет уравнение cos2x x 3 2

Алгебра | 10 — 11 классы

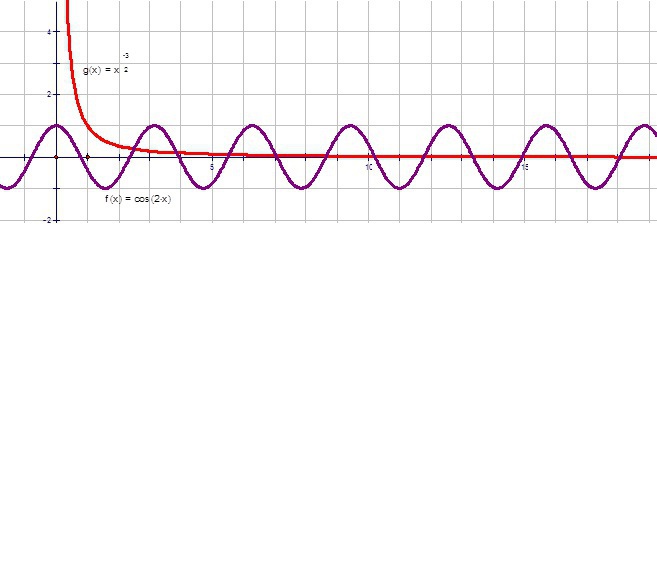
C помощью графика функции выяснить, сколько корней имеет уравнение cos2x = x ^ ( — 3 / 2).

Видео:§40 Свойства функции y = cos x и её графикСкачать

Выясни, сколько корней имеет уравнение x ^ 2 + x + 3 = 0?

Выясни, сколько корней имеет уравнение x ^ 2 + x + 3 = 0.

Видео:Построение графика функции y=cos 2xСкачать

С помощью графиков выясните сколько корней имеет уравнение [tex] sqrt = (x — 2)[ / tex] ^ 2?

С помощью графиков выясните сколько корней имеет уравнение [tex] sqrt = (x — 2)[ / tex] ^ 2.

Видео:10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать

Сколько корней имеет уравнение sinx + cosx = 1 на [ — п ; п]?

Сколько корней имеет уравнение sinx + cosx = 1 на [ — п ; п].

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Выясните сколько корней имеет квадратное уравнение 2x ^ 2 — 8x + 8 = 4?

Выясните сколько корней имеет квадратное уравнение 2x ^ 2 — 8x + 8 = 4.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Выясните с помощью графиков, сколько корней имеет уравнение х 2 + 1 = — х?

Выясните с помощью графиков, сколько корней имеет уравнение х 2 + 1 = — х.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

C помощью схематических графиков выясните, сколько корней имеет уравнение x ^ 2 + 1 = — x?

C помощью схематических графиков выясните, сколько корней имеет уравнение x ^ 2 + 1 = — x.

Видео:График функции y=sinx и ее свойства. 10 класс.Скачать

Выясните с помощью графиков, сколько корней имеет уравнение х 2 + 1 = — х?

Выясните с помощью графиков, сколько корней имеет уравнение х 2 + 1 = — х.

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Построить график функцииy = <3x + 7, если x2Используя график функции укажите сколько корней имеет уравнение y(x) = a при различных значениях а?

Построить график функции

Используя график функции укажите сколько корней имеет уравнение y(x) = a при различных значениях а.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Выясните, сколько корней имеет уравнениеx ^ 4 + 6x ^ 2 — 4 = 0?

Выясните, сколько корней имеет уравнение

x ^ 4 + 6x ^ 2 — 4 = 0.

Видео:Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

Выясните имеет ли корни уравнение и сколько : 28 — 20х = 2х + 25 — 16х — 12 — 6х?

Выясните имеет ли корни уравнение и сколько : 28 — 20х = 2х + 25 — 16х — 12 — 6х.

Вы открыли страницу вопроса C помощью графика функции выяснить, сколько корней имеет уравнение cos2x = x ^ ( — 3 / 2)?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

180 — 39 = 141 141 : 2 = 70, 5.

S(t) = — 3t³ — 2t² + 6t + 4. V = S⁾ = — 3 * 3t² — 2 * 2t + 6 = — 9t² — 4t + 6 v(2) = — 9 * 2² — 4 * 2 + 6 = — 36 — 8 + 6 = — 38 м / с a = v⁾ = — 9 * 2t — 4 = — 18t — 4 a(2) = — 18 * 2 — 4 = — 40 м / с².

5 * х — 7 = х + 5 5 * 3 = 15(это 1 ящик) 5х — х = 5 + 73 + 5 = 8(это 2 ящик) 4х = 12 х = 3 Проверка : 5 * 3 — 7 = 3 + 5 Ответ : В начале впервом ящике было 15 яблок, А во втором ящике было 8 яблок КАЖЕТСЯ ТАК.

I)(a / m² + a² / m³) / (m² / a² + m / a) = (a / m² / m² / a² + a² / m³ / m² / a² + m / a / a / m² + m / a / a² / m³) = (a / m²÷a² / m² + a² / m³÷a² / m² + m / a÷m² / a + m / a÷m³ / a²) = (a³ / m⁴ + a⁴ / m⁵ + m³ / a² + m⁴ / a³) = ((a³a³m / m⁴ma³ + a⁴a..

На координатной плоскости хОу постройте график уравнения : 2х — у + 5 = 0 прямая, y = 2x + 5 проходит через точки, например, A( 0 ; 5)и B(1 ; 7) на координатной плоскости изображаемA( 0 ; 5)иB(1 ; 7), проводим через них прямую при помощи линейки.

(4х + 2) / 3 = (5х + 1) / 6 8х + 4 = 5х + 1 8х — 5х = 1 — 4 3х = — 3 х = — 3 : 3 х = — 1.

Решается путём замены. На примере Б. Разница будет только в замене. Предположим, что один из корней сокрыт в одном из делителей свободного члена (свойство Бинома Ньютона) : Предположим, что это число 3. Тогда, если подставить это число в выраже..

S (проекции Δ) = S(Δ)·cos45° = 18·√2 / 2 = 9√2 (см²).

7) 96% — 1152р 100% — хр х = 100×1152÷96 = 1200р Ответ : 1200р.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

С помощью графика функции выяснить сколько корней имеет уравнение cos2x x 3 2

Вопрос по алгебре:

C помощью графика функции выяснить, сколько корней имеет уравнение cos2x=x^(-3/2)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:Построение графика функции y = cos xСкачать

Применение производной для решения нелинейных уравнений и неравенств

п.1. Количество корней кубического уравнения

Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. begin f(x)=ax^3+bx^2+cx+d\ f'(x)=3ax^2+bx+c end Если в уравнении (f'(x)=0) дискриминант (D=4b^2-12ac=4(b^2-3ac)gt 0), кубическая парабола имеет две точки экстремума: (x_=frac<-2bpmsqrt>). Если при этом значения функции в точках экстремума (f(x_1)cdot f(x_2)lt 0), т.е. расположены по разные стороны от оси OX, парабола имеет три точки пересечения с этой осью. Исходное уравнение имеет три корня.
Если две точки экстремума найдены, но (f(x_1)cdot f(x_2)=0), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.

Пример 1. Сколько корней имеют уравнения:

1) (x^3+3x^2-4=0) (b^2-3ac=9gt 0 (c=0) ) (f(x)=x^3+3x^2-4 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-4, f(x_2)=0 ) (f(x_1)cdot f(x_2)=0Rightarrow) два корня	2) (x^3+3x^2-1=0) (b^2-3ac=9gt 0 ) (f(x)=x^3+3x^2-1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=-1, f(x_2)=3 ) (f(x_1)cdot f(x_2)lt 0Rightarrow) три корня
3) (x^3+3x^2+1=0) (b^2-3ac=9gt 0) (f(x)=x^3+3x^2+1 ) (f'(x)=3x^2+6x=3x(x+2) ) (x_1=0, x_2=-2 ) (f(x_1)=1, f(x_2)=5 ) (f(x_1)cdot f(x_2)gt 0Rightarrow) один корень	4) (x^3+x^2+x+3=0) (b^2-3ac=1-3lt 0 ) Один корень

п.2. Количество корней произвольного уравнения

Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.

Пример 2. а) Найдите число корней уравнения (frac 1x+frac+frac)
б) Найдите число корней уравнения (frac 1x+frac+frac=k)

Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью (y=1). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=frac1x+frac+frac $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: (xneleft)
Все три точки – точки разрыва 2-го рода. begin lim_left(frac1x+frac+fracright)=-infty-1-frac13=-infty\ lim_left(frac1x+frac+fracright)=+infty-1-frac13=+infty\ lim_left(frac1x+frac+fracright)=1-infty-frac12=-infty\ lim_left(frac1x+frac+fracright)=1+infty-frac12=+infty\ lim_left(frac1x+frac+fracright)=frac13+frac12-infty=-infty\ lim_left(frac1x+frac+fracright)=frac13+frac12+infty=+infty end 2) Функция ни четная, ни нечетная.
Функция непериодическая.
3) Асимптоты
1. Вертикальные (x=0, x=1, x=3) – точки разрыва 2-го рода
2. Горизонтальные: begin lim_left(frac1x+frac+fracright)=-0-0-0=-0\ lim_left(frac1x+frac+fracright)=+0+0+0=+0\ end Горизонтальная асимптота (y=0)
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: (k=0), нет.
4) Первая производная $$ f'(x)=-frac-frac-fraclt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.

5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.

6) Точки пересечения с OY – нет, т.к. (x=0) – асимптота
Точки пересечения с OX – две, (0lt x_1lt 1,1lt x_2lt 3)

7) График

Получаем ответ для задачи (а) 3 корня.

Решаем более общую задачу (б). Передвигаем горизонталь (y=k) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При (klt 0) — три корня
При (k=0) — два корня
При (kgt 0) — три корня

Ответ: а) 3 корня; б) при (k=0) два корня, при (kne 0) три корня.

Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ sqrt+sqrt=a $$ имеет по крайней мере одно решение.

Исследуем функцию (f(x)=sqrt+sqrt)
ОДЗ: ( begin x-1geq 0\ 10-2xgeq 0 end Rightarrow begin xgeq 1\ xleq 5 end Rightarrow 1leq xleq 5 )
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: (f(1)=0+sqrt=2sqrt, f(5)=sqrt+0=2)
Первая производная: begin f'(x)=frac<2sqrt>+frac<2sqrt>=frac<2sqrt>-frac<sqrt>\ f'(x)=0 text 2sqrt=sqrtRightarrow 4(x-1)=10-2xRightarrow 6x=14Rightarrow x=frac73\ fleft(frac73right)=sqrt+sqrt=sqrt+sqrt<frac>=frac<sqrt>=2sqrt end Промежутки монотонности:

Можем строить график:

(y=a) — горизонтальная прямая.
Количество точек пересечения (f(x)) и (y) равно количеству решений.
Получаем:

По крайней мере одно решение будет в интервале (2leq aleq 2sqrt).

п.3. Решение неравенств с построением графиков

Пример 4. Решите неравенство (fracgt frac)

Разобьем неравенство на совокупность двух систем.
Если (xgt 1), то (x-1gt 0), на него можно умножить слева и справа и не менять знак.
Если (xlt 1), то (x-1lt 0), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: (xgt 0)

Получаем совокупность: begin left[ begin begin xgt 1\ 2+log_3 xgtfrac end \ begin 0lt xlt 1\ 2+log_3 xltfrac end end right. \ 2+log_3 xgt fracRightarrow log_3 xgt fracRightarrow log_3 xgt frac\ left[ begin begin xgt 1\ log_3 xgtfrac end \ begin 0lt xlt 1\ log_3 xltfrac end end right. end Исследуем функцию (f(x)=frac=frac=1-frac)
Точка разрыва: (x=frac12) – вертикальная асимптота
Односторонние пределы: begin lim_left(1-fracright)=1-frac=+infty\ lim_left(1-fracright)=1-frac=-infty end Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: (y=1) begin lim_left(1-fracright)=1-frac=1+0\ lim_left(1-fracright)=1-frac=1-0 end На минус бесконечности кривая стремится к (y=1) сверху, а на плюс бесконечности – снизу.
Первая производная: $$ f'(x)=left(1-fracright)’=fracgt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-frac $$ Одна критическая точка 2-го порядка (x=frac12)

💡 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

ФУНКЦИЯ y = √¯x ( корень из х ) МАТЕМАТИКАСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Исследование функции. 10 класс.Скачать

Математический анализ, 15 урок, АссимптотыСкачать

Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать