С чего начать изучение тригонометрических уравнений

Видео:ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

• Синус угла – отношение противолежащего катета к гипотенузе;
• Косинус угла – отношение прилежащего катета к гипотенузе;
• Тангенс угла – отношение противолежащего катета к прилежащему;
• Котангенс угла – отношение прилежащего катета к противолежащему.

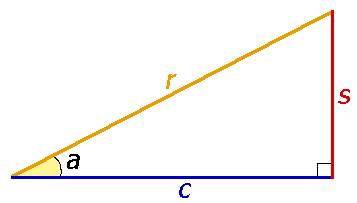
Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°	30°	45°	60°	90°
sin	0	1	√3	–
ctg	–	√3	1	Принцип повтора знаков тригонометрических функций Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:Тригонометрия в ЕГЭ может быть простойСкачать Тригонометрический круг Углы в радианах Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. Видео:Вся Тригонометрия для Чайников, 10 класс, урок 1Скачать Геометрия. Урок 1. Тригонометрия Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно. Видео-уроки на канале Ёжику Понятно. Подпишись! Содержание страницы: Видео:Математика это не ИсламСкачать Тригонометрия в прямоугольном треугольнике Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий. Синус угла – отношение противолежащего катета к гипотенузе. sin α = Противолежащий катет гипотенуза Косинус угла – отношение прилежащего катета к гипотенузе. cos α = Прилежащий катет гипотенуза Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу). tg α = Противолежащий катет Прилежащий катет Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу). ctg α = Прилежащий катет Противолежащий катет Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °: sin ∠ A = C B A B cos ∠ A = A C A B tg ∠ A = sin ∠ A cos ∠ A = C B A C ctg ∠ A = cos ∠ A sin ∠ A = A C C B sin ∠ B = A C A B cos ∠ B = B C A B tg ∠ B = sin ∠ B cos ∠ B = A C C B ctg ∠ B = cos ∠ B sin ∠ B = C B A C Видео:12 часов Тригонометрии с 0.Скачать Тригонометрия: Тригонометрический круг Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга. Тригонометрический круг – это окружность единичного радиуса с центром в начале координат. Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 ) На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы. Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A . Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) . Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y . Рассмотрим прямоугольный треугольник A O B : cos α = O B O A = O B 1 = O B sin α = A B O A = A B 1 = A B Поскольку O C A B – прямоугольник, A B = C O . Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат). Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° : Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный . Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y . Координата по оси x – косинус угла , координата по оси y – синус угла . Ещё одно замечание. Синус тупого угла – положительная величина, а косинус – отрицательная. Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный . Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный . Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать Основное тригонометрическое тождество sin 2 α + cos 2 α = 1 Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B : A B 2 + O B 2 = O A 2 sin 2 α + cos 2 α = R 2 sin 2 α + cos 2 α = 1 Видео:ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать Тригонометрия: Таблица значений тригонометрических функций	0 °	30 °	45 °	60 °	90 °
sin α	0	1 2	2 2	3 2	1
cos α	1	3 2	2 2	1 2	0
tg α	0	3 3	1	3	нет
ctg α	нет	3	1	3 3	0

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:Тригонометрические уравнения | Борис ТрушинСкачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:А ты знаешь, когда в тригонометрических уравнениях писать пk, а когда 2пk? #математика #егэ2023 #егэСкачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Видео:Когда начинать готовиться к ЕГЭ?Скачать

Способы решения тригонометрических уравнений. 10-й класс

Разделы: Математика

Класс: 10

«Уравнения будут существовать вечно».

Цели урока:

• Образовательные:
  • углубление понимания методов решения тригонометрических уравнений;
  • сформировать навыки различать, правильно отбирать способы решения тригонометрических уравнений.
• Воспитательные:
  • воспитание познавательного интереса к учебному процессу;
  • формирование умения анализировать поставленную задачу;
  • способствовать улучшению психологического климата в классе.
• Развивающие:
  • способствовать развитию навыка самостоятельного приобретения знаний;
  • способствовать умению учащихся аргументировать свою точку зрения;

Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.

1 урок

I. Актуализация опорных знаний

Устно решить уравнения:

1) cosx = 1;
2) 2 cosx = 1;
3) cosx = –;
4) sin2x = 0;
5) sinx = –;
6) sinx = ;
7) tgx = ;
8) cos 2 x – sin 2 x = 0

1) х = 2к;
2) х = ± + 2к;
3) х =± + 2к;
4) х = к;
5) х = (–1) + к;
6) х = (–1) + 2к;
7) х = + к;
8) х = + к; к Z.

II. Изучение нового материала

– Сегодня мы с вами рассмотрим более сложные тригонометрические уравнения. Рассмотрим 10 способов их решения. Далее будет два урока для закрепления, и на следующий урок будет проверочная работа. На стенде «К уроку» вывешены задания, аналогичные которым будут на проверочной работе, надо их прорешать до проверочной работы. (Накануне, перед проверочной работой, вывесить на стенде решения этих заданий).

Итак, переходим к рассмотрению способов решения тригонометрических уравнений. Одни из этих способов вам, наверное, покажутся трудными, а другие – лёгкими, т.к. некоторыми приёмами решения уравнений вы уже владеете.

Четверо учащихся класса получили индивидуальное задание: разобраться и показать вам 4 способа решения тригонометрических уравнений.

(Выступающие учащиеся заранее подготовили слайды. Остальные учащиеся класса записывают основные этапы решения уравнений в тетрадь.)

1 ученик: 1 способ. Решение уравнений разложением на множители

sin 4x = 3 cos 2x

Для решения уравнения воспользуемся формулой синуса двойного угла sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.

2x = + к, к Z или sin 2x = 1,5 – нет решений, т.к | sin| 1
x = + к; к Z.
Ответ: x = + к , к Z.

2 ученик. 2 способ. Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение

cos 3x + sin 2x – sin 4x = 0.

Для решения уравнения воспользуемся формулой sin– sin = 2 sin сos

cos 3x + 2 sin сos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений:

Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит

Ответ:

3 ученик. 3 способ. Решение уравнений преобразованием произведения тригонометрических функций в сумму

sin 5x cos 3x = sin 6x cos2x.

Для решения уравнения воспользуемся формулой

Ответ:

4 ученик. 4 способ. Решение уравнений, сводящихся к квадратным уравнениям

3 sin x – 2 cos 2 x = 0,
3 sin x – 2 (1 – sin 2 x ) = 0,
2 sin 2 x + 3 sin x – 2 = 0,

Пусть sin x = t, где | t |. Получим квадратное уравнение 2t 2 + 3t – 2 = 0,

. Таким образом . не удовлетворяет условию | t |.

Значит sin x = . Поэтому .

Ответ:

III. Закрепление изученного по учебнику А. Н. Колмогорова

1. № 164 (а), 167 (а) (квадратное уравнение)
2. № 168 (а) (разложение на множители)
3. № 174 (а) (преобразование суммы в произведение)
4. (преобразование произведения в сумму)

(В конце урока показать решение этих уравнений на экране для проверки)

№ 164 (а)

2 sin 2 x + sin x – 1 = 0.
Пусть sin x = t, | t | 1. Тогда
2 t 2 + t – 1 = 0, t = – 1, t= . Откуда

Ответ: –.

№ 167 (а)

3 tg 2 x + 2 tg x – 1 = 0.

Пусть tg x = 1, тогда получим уравнение 3 t 2 + 2 t – 1 = 0.

Ответ:

№ 168 (а )

Ответ:

№ 174 (а )

Ответ:

Решить уравнение:

Ответ:

2 урок (урок-лекция)

IV. Изучение нового материала (продолжение)

– Итак, продолжим изучение способов решения тригонометрических уравнений.

5 способ. Решение однородных тригонометрических уравнений

Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.

sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin 2 x + cos 2 x = 1.

Получим tg x – 1 = 0.

Ответ:

Уравнения вида a sin 2 x + bcos 2 x + c sin x cos x = 0 , где a, b, c –некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.

sin 2 x – 3 sin x cos x + 2 cos 2 = 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.

tg 2 x – 3tg x + 2 = 0.

Пусть tg x = t. D = 9 – 8 = 1.

тогда Отсюда tg x = 2 или tg x = 1.

В итоге x = arctg 2 + , x =

Ответ: arctg 2 + ,

Рассмотрим ещё одно уравнение: 3 sin 2 x – 3 sin x cos x + 4 cos 2 x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin 2 x + cos 2 x). Тогда получим:
3sin 2 x – 3sin x cos x + 4cos 2 x = 2 · (sin 2 x + cos 2 x),
3sin 2 x – 3sin x cos x + 4cos 2 x – 2sin 2 x – 2 cos 2 x = 0,
sin 2 x – 3sin x cos x + 2cos 2 x = 0. (Получили 2 уравнение, которое уже разобрали).

Ответ: arctg 2 + k,

6 способ. Решение линейных тригонометрических уравнений

Линейным тригонометрическим уравнением называется уравнение вида a sin x + b cos x = с, где a, b, c – некоторые числа.

Рассмотрим уравнение sin x + cos x = – 1.
Перепишем уравнение в виде:

Учитывая, что и, получим:

Ответ:

7 способ. Введение дополнительного аргумента

Выражение a cos x + b sin x можно преобразовать:

.

(это преобразование мы уже ранее использовали при упрощении тригонометрических выражений)

Введём дополнительный аргумент – угол такой, что

Тогда

Рассмотрим уравнение: 3 sinx + 4 cosx = 1.

Учтём, что . Тогда получим

0,6 sin x + 0,8 cosx = 1. Введём дополнительный аргумент – угол такой, что , т.е. = arcsin 0,6. Далее получим

Ответ: – arcsin 0,8 + +

8 способ. Уравнения вида Р

Такого рода уравнения удобно решать при помощи введения вспомогательной переменной t = sin x ± cosx. Тогда 1 ± 2 sinx cosx = t 2 .

Решить уравнение: sinx + cosx + 4 sinx cosx – 1 = 0.

Введём новую переменную t = sinx + cosx, тогда t 2 = sin 2 x + 2sin x cos x + cos 2 = 1 + 2 sin x cos x Откуда sin x cos x = . Следовательно получим:

t + 2 (t 2 – 1) – 1 = 0.
2 t 2 + t – 2 – 1 = 0,
2 t 2 + t – 3 = 0..Решив уравнение, получим = 1, =.

sinx + cosx = 1 или sinx + cosx =

Ответ:

9 способ. Решение уравнений, содержащих тригонометрические функции под знаком радикала.

Решить уравнение:

В соответствии с общим правилом решения иррациональных уравнений вида, запишем систему, равносильную исходному уравнению:

Решим уравнение 1 – cos x = 1 – cos 2 x.

1 – cos x = 1 – cos 2 x,
1 – cos x – (1 – cos x) (1 + cos x) = 0,
(1 – cos x) (1 – 1 – cos x) = 0,
– (1 – cos x) cos x = 0.

Условию удовлетворяют только решения

Ответ:

10 способ. Решение уравнений с использованием ограниченности тригонометрических функций y = sin x и y = cos x.

Решить уравнение: sin x + sin 9x = 2.
Так как при любых значениях х sin x 1, то данное уравнение равносильно системе:

Решение системы

Ответ:

V. Итог урока

Таким образом мы сегодня рассмотрели 10 различных способов решения тригонометрических уравнений. Безусловно, многие из приведённых задач могут быть решены несколькими способами.

(Пятерым наиболее подготовленным учащимся , а также всем желающим дать индивидуальное творческое задание: найти различные способы решения тригонометрического уравнения sinx + cosx = 1 )

Домашнее задание: № 164 -170 (в, г).

📺 Видео

Все методы решения тригонометрических уравнений за 30 минутСкачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Решение тригонометрических уравнений. Вебинар | МатематикаСкачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Решение тригонометрических уравнений. 10 класс.Скачать