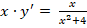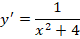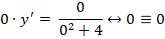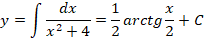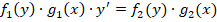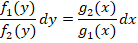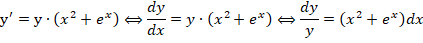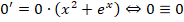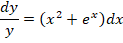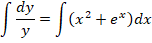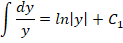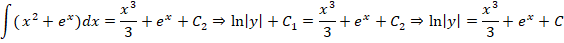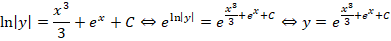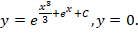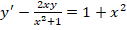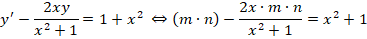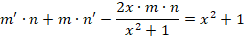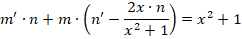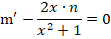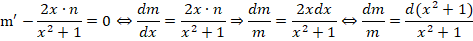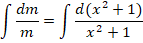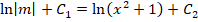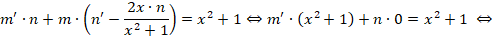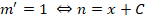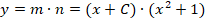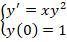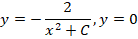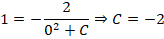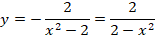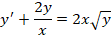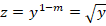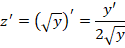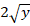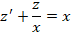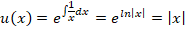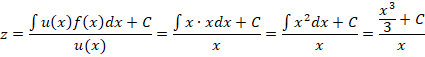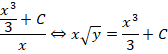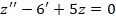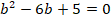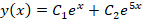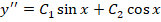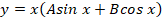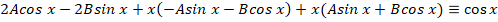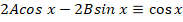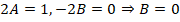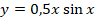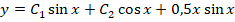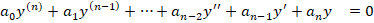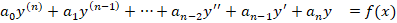С чего начать изучение дифференциальных уравнений

Видео:Математика это не ИсламСкачать

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Видео:Как решают уравнения в России и СШАСкачать

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Дифференциальные уравнения (ДУ) — методы и примеры решения уравнений разного порядка

Многих людей, хоть как-то изучавших курс высшей математики в учебном заведении, приводит в ужас словосочетание «дифференциальные уравнения». Согласно строгому научному определению в книгах – так именуются математические выражения, где в состав входят функция, ее производная или параметр. Имеется достаточно большое количество типов этих равенств, рассмотрим подходы к их решению так, чтобы они были понятны даже для «чайников».

Видео:Дифференциальные уравнения. 11 класс.Скачать

Дифференциальные уравнения первого порядка

Обыкновенное диффуравнение (ДУ) 1-го порядка задается относительно некой функции, имеющей вид у(х):

здесь, F(x,y,y ’ ) – это функция, задающаяся для трех аргументов (в этом примере для х, у и у ’ ).Таково строгое математическое определение ДУ.

Для примера можно привести следующее уравнение:

функция вида F(x,y,p) = xp — y 2

Простейшие ДУ первого порядка

Общепринятый механизм нахождения решения таких выражений (чаще всего похожи на y’ = f(x)) – это интегрирование левой и правой части такого уравнения на заданном промежутке Х.

После интегрирования получим такое выражение:

Воспользовавшись свойствами, которые относятся к интегральным выражениям, упростим выражение до вида:

здесь, F(x) – это первообразная от функции f(x) на заданном интервале Х, а N – случайным образом выбранная константа.

Задача №1

Необходимо определить все возможные варианты решения диффуравнения, имеющего вид

Последовательно рассмотрим решение.

Представленное диффуравнение может иметь смысл только при действительных значениях параметра х. Примем условие, что x ≠ 0, тогда выражение легко преобразовывается в следующее:

Если же, напротив, принять, что х = 0, то выражение приобретет следующий вид, характерный для любых функций y’, удовлетворяющих данному условию:

Можно заключить, что решением при справедливости условия х = 0 будет любая функция у, найденная, когда аргумент равен нулю. Остается только проинтегрировать полученное диффуравнение:

Данное выражение – это решение для приведенного диффуравнения.

ДУ с разделяющимися переменными

Среди дифуров 1-го порядка можно выделить такие, где все переменные х и у можно преобразовать так, что они окажутся по разные стороны от знака равенства.

Соответственно уравнения, где путем преобразований это возможно сделать, называются диффуравнениями с разделяющимися переменными.

Их общий вид следующий:

После проведения нескольких преобразований, это выражение может быть сведено к следующему виду:

При составлении преобразований необходимо внимательно разделять переменные, не допуская, чтобы функции обращались в ноль, иначе возможна потеря некоторых значений.

Задача №2

Рассмотрим обыкновенный пример. Необходимо определить все возможные решения диффуравнения y’ = y(x 2 + e x )

Как решать? В первую очередь проводим разделение переменных в разные части уравнения:

Данные преобразования справедливы, если у ≠ 0.

Если рассмотреть вариант решения при нулевом показателе функции, то можно заметить ,что

Это означает, что y = 0 – одно из возможных решений задачи.

Рассмотрим другие варианты решений, для чего произведем интегрирование диффуравнения:

Финальная часть преобразований будет вторым решением диффуравнения. Останется только потенциировать это выражение, чтобы привести его к более явному виду:

Правильными решениями, в результате преобразований, будут:

Кроме того, можно воспользоваться онлайн системой для нахождения ответа. Подробные объяснения даны в решебниках Филиппова и Понтрягина.

Линейные неоднородные ДУ первого порядка

Линейные неоднородные уравнения – это такие выражения, которые можно записать в формате y’ + b(x)y = f(x), при этом функции b(x) и f(x) – непрерывные.

Основной принцип при нахождении решения сводится к следующим шагам:

Первым делом для уравнения необходимо произвести поиск решения, которое бы соответствовало линейному однородному диффуравнению.

Затем необходимо варьировать произвольной постоянной, производя ее замену на функцию.

На финальном этапе функция подставляется в первоначальное уравнение, откуда, решая ДУ, получается ответ.

Задача №3

Рассмотрим применение методики решения на примере.

Необходимо найти решение дифференциального уравнения вида

Решение заключается в следующем. Первоначально примем, что y = m∗n, следовательно, получается:

На следующем этапе нужно определить, что такое m (оно обязательно не должно быть равным нулю), при котором все выражение внутри скобок будет равно нулю.

Получаем дополнительное дифференциальное уравнение:

Теперь необходимо принять одно из частных решений n = x 2 + 1, которое соответствует равенству С₂ — С₁=0.

Выполняем оставшиеся преобразования:

Вполне очевидно, что ответом на условие задачи будет функция:

Задача Коши для ДУ

При рассмотрении решения практически любого диффуравнения, имеющего вид F(m,n,n’) = 0, становится очевидно, что это бесконечно большое количество решений (это следствие самого возникновения диффуравнения).

На данном этапе математики сталкиваются с вопросом о выборе конкретного решения и способе его выделения из множества.Иными словами, если представить решения в виде бесконечного множества интегральных кривых, то необходимо найти среди них нужную.

Чтобы это сделать, необходимо рассмотреть плоскость X_oy, где должна быть задана некая точка D₀, имеющая координаты (x₀, y₀) – именно через них и должна пройти интегральная кривая, чтобы стать искомым ответом.

Когда мы с самого начала задаем точку D₀(x₀, y₀) – это означает, задание начального условия y(x₀) = y₀. Диффуравнение, для которого определено начальное условие в представленном формате, называется уравнением с заданной задачей Коши.

Задача №4

Рассмотрим примеры с объяснениями. Необходимо определить решения задачи Коши вида:

Ход решения строится в три этапа. На первом этапе решаем диффуравнение y’ = xy 2 стандартным методом. Его решение приводить не будем, приведем только ответ:

Производим подстановку начального значения (х = 0, у = 1) в решение и находим значение С:

Производим подстановку полученного значения в ответ диффуравнения и получаем одно из частных решений:

Полученная функция – ответ на задачу Коши в этом примере.

Дифференциальные уравнения Бернулли

ДУ Бернулли обычно представлено в следующем виде:

Обязательное условие, что функции b(x) и c(x) – являются непрерывными.

Задача №5

Рассмотрим общее решение данного типа на примере. Необходимо выполнить поиск всех возможных решений уравнения:

Во время оценки уравнения в нем можно идентифицировать ДУ Бернулли с параметром ½. Оно легко сводится к линейному ДУ, для этого достаточно заменить выражения:

Выполним деление по начальному уравнению Бернулли на

и выполним необходимые преобразования:

Произведем замену параметра х на параметр у:

Теперь вычисляем интегрирующий модуль для данной функции, он будет равен:

Теперь производим ряд преобразований для вычисления решения диффуравнения:

Переписываем полученную функцию в неявном виде и получаем ответ:

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения второго порядка

Отличить ДУ 2-го порядка от таковых 1-го порядка достаточно просто – в их составе присутствует вторая производная (y’’) и не содержится производных более высокого уровня.

Общий вид таких уравнений таков:

Линейные однородные ДУ второго порядка с постоянными коэффициентами

Определение линейных дифференциальных однородных уравнений 2-го порядка крайне просто – они имеют вид:

При это важным условием теории является причисление r и k к действительным числам.

Задача №6

Рассмотрим решение однородных диффуравнений 2-го порядка с постоянными коэффициентами на примере.

Найти решение диффуравнения 2-го порядка вида:

Во всех таких случаях начинаем с поиска характеристического уравнения:

Методы решения данного уравнения достаточно простые, можно воспользоваться калькулятором или быстро решить на листочке, поэтому их приводить не будем, запишем лишь корни – 1, 5.

Поскольку это все действительные, неодинаковые числа, то можно записать функцию-решение в следующем виде:

Линейные неоднородные ДУ второго порядка с постоянными коэффициентами

Общий вид неоднородных диффуравнений второго порядка легко определить по представленному образцу:

Переменные r и k должны быть вещественными и постоянными числами.

Задача №7

Рассмотрим подробное решение. Необходимо определить все решения для уравнения y» + y = cos x.

На первом этапе находим в составе неоднородного уравнения его однородную часть – это будет y» — y = 0.

Для него уже выполняем поиск характеристического уравнения – оно будет иметь вид k 2 + 1 = 0.

Корнями для данного характеристического уравнения являются k₁ = -i и k₂ = i.

Исходя из этого записываем решение для однородного уравнения:

Из-за отсутствия параметра с производной первого порядка также будет справедливо записать:

Теперь остается только подставить найденные выражения:

Частное и общее решение для уравнения можно записать:

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения высших порядков

Дифференциальные однородные уравнения высших порядков легко отличить, если они совпадают со следующим видом:

Для неоднородных справедлив другой формат:

Для выбора корректного пути решения ДУ, необходимо четко и правильно определить его тип.

Для этого необходимо решить уравнение относительно его производной и проверить, возможно ли разложение функции на множители. После этого достаточно сравнить с одним из типов, приведенным в данной статье.

Видео:Как распознать талантливого математикаСкачать

Что такое дифференциальное уравнение и зачем оно нужно?

На сегодняшний день одним из важнейших навыков для любого специалиста является умение решать дифференциальные уравнения. Решение дифференциальных уравнений – без этого не обходится ни одна прикладная задача, будь это расчет какого-либо физического параметра или моделирование изменений в результате принятой макроэкономической политики. Эти уравнения также важны для ряда других наук, таких как химия, биология, медицина и т.д. Ниже мы приведем пример использования дифференциальных уравнений в экономике, но перед этим кратко расскажем об основных типах уравнений.

Видео:Простейшие дифференциальные уравненияСкачать

Дифференциальные уравнения – простейшие виды

Мудрецы говорили, что законы нашей вселенной написаны на математическом языке. Конечно, в алгебре есть много примеров различных уравнений, но это, большей частью, учебные примеры, неприменимые на практике. По-настоящему интересная математика начинается, когда мы хотим описать процессы, протекающие в реальной жизни. Но как отразить фактор времени, которому подчиняются реальные процессы – инфляция, выработка продукции или демографические показатели?

Вспомним одно важное определение из курса математики, касающееся производной функции. Производная является скоростью изменения функции, следовательно, она может помочь нам отразить фактор времени в уравнении.

То есть, мы составляем уравнение с функцией, которая описывает интересующий нас показатель и добавляем в уравнение производную этой функции. Это и есть дифференциальное уравнение. А теперь перейдем к простейшим типам дифференциальных уравнений для чайников.

Простейшее дифференциальное уравнение имеет вид $y’(x)=f(x)$, где $f(x)$ – некоторая функция, а $y’(x)$ – производная или скорость изменения искомой функции. Оно решается обычным интегрированием: $$y(x)=int f(x)dx.$$

Второй простейший тип называется дифференциальным уравнением с разделяющимися переменными. Такое уравнение выглядит следующим образом $y’(x)=f(x)cdot g(y)$. Видно, что зависимая переменная $y$ также входит в состав конструируемой функции. Уравнение решается очень просто – нужно «разделить переменные», то есть привести его к виду $y’(x)/g(y)=f(x)$ или $dy/g(y)=f(x)dx$. Остается проинтегрировать обе части $$int frac=int f(x)dx$$ – это и есть решение дифференциального уравнения разделяющегося типа.

Последний простой тип – это линейное дифференциальное уравнение первого порядка. Оно имеет вид $y’+p(x)y=q(x)$. Здесь $p(x)$ и $q(x)$ – некоторые функции, а $y=y(x)$ – искомая функция. Для решения такого уравнения применяют уже специальные методы (метод Лагранжа вариации произвольной постоянной, метод подстановки Бернулли).

Есть более сложные виды уравнений – уравнения второго, третьего и вообще произвольного порядка, однородные и неоднородные уравнения, а также системы дифференциальных уравнений. Для их решения нужна предварительная подготовка и опыт решения более простых задач.

Большое значение для физики и, что неожиданно, финансов имеют так называемые дифференциальные уравнения в частных производных. Это значит, что искомая функция зависит от нескольких переменных одновременно. Например, уравнение Блека-Шоулса из области финансового инжиниринга описывает стоимость опциона (вид ценной бумаги) в зависимости от его доходности, размера выплат, а также сроков начала и конца выплат. Решение дифференциального уравнения в частных производных довольно сложное, обычно нужно использовать специальные программы, такие как Matlab или Maple.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Пример применения дифференциального уравнения в экономике

Приведем, как и было обещано, простой пример решения дифференциального уравнения. Вначале поставим задачу.

Для некоторой фирмы функция маржинальной выручки от продажи своей продукции имеет вид $MR=10-0,2q$. Здесь $MR$ – маржинальная выручка фирмы, а $q$ – объем продукции. Нужно найти общую выручку.

Как видно из задачи, это прикладной пример из микроэкономики. Множество фирм и предприятий постоянно сталкивается с подобными расчетами в ходе своей деятельности.

Приступаем к решению. Как известно из микроэкономики, маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж.

С математической точки задача свелась к решению дифференциального уравнения $R’=10-0,2q$ при условии $R(0)=0$.

Проинтегрируем уравнение, взяв первообразную функцию от обеих частей, получим общее решение: $$R(q) = int (10-0,2q)dq = 10 q-0,1q^2+C. $$

Чтобы найти константу $C$, вспомним условие $R(0)=0$. Подставим: $$R(0) =0-0+C = 0. $$ Значит C=0 и наша функция общей выручки принимает вид $R(q)=10q-0,1q^2$. Задача решена.

Другие примеры по разным типам ДУ собраны на странице: Дифференциальные уравнения с решениями онлайн.

🔥 Видео

13. Как решить дифференциальное уравнение первого порядка?Скачать

Высшая математика. Рисую дерево вышматаСкачать

День студента мехмата МГУ #мгу #умскул #физика #математика #учеба #подготовкаогэ #подготовкакегэСкачать

1. Что такое дифференциальное уравнение?Скачать