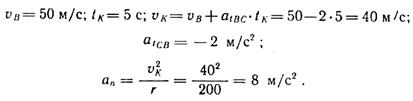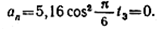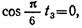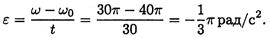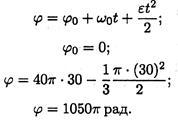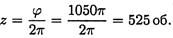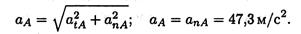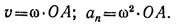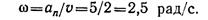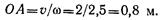Тело вращается вокруг точки О. Определим параметры движения точки А, расположенной на расстоянии r а от оси вращения (рис. 11.6, 11.7).
Примеры решения задач
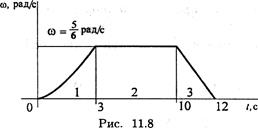
Пример 1. По заданному графику угловой скорости (рис.11.8)определить вид вращательного движения.
Решение
1. Участок 1 — неравномерное ускоренное движение,
2. Участок 2 — скорость постоянна — движение равномерное, ω = const.
3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, е = ω /
Число оборотов за 30 с:
2. Определяем время до полной остановки.
Скорость при остановке равна нулю, ω = 0.
Пример 5. Маховое колесо вращается равномерно со скоростью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить скорость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.
Решение
 |
Касательное ускорение точки A atA = 0; нормальное ускорение точки А аnA = ω 2 rA
апA = (12,56) 2 • 0,3 = 47,3м/с 2 . 5. Полное ускорение точек на ободе колеса
Пример 6. Точка начала двигаться равноускорено по прямой из состояния покоя и через 25 с ее скорость стала равна 50 м/с. С этого момента точка начала равнозамедленное движение по дуге окружности радиуса г = 200 м и через 20 с ее скорость снизилась до 10 м/с. После этого точка продолжила свое движение с этой скоростью по прямой и через 5 с внезапно остановилась.
Определить: 1) среднюю скорость точки на всем пути;
2) полное ускорение точки через 10 с после начала ее равнозамедленного движения по окружности.
Решение
1. 
Представим траекторию движения точки, как показано на рис. 5. Весь путь, пройденный точкой, разбиваем на участки равноускоренного (по отрезку АВ), равнозамедленного (по дуге ВС) и равномерного (по отрезку CD) движения.
2. Рассмотрим движения точки по отрезку АВ:
3. Рассмотрим движение точки по дуге ВС:
4. Рассмотрим движение точки на отрезке CD:
5. Определим среднюю скорость точки на всем пути по траектории движения ABCD (см. рис. 5):
tABCD = tAB + tBC + tCD = 25 + 20 + 5 = 50 c
6. Определим значение полного ускорения точки через 5 с после начала равнозамедленного движения (см. положение К на рис. 5)
Пример 7.Тело начало вращаться из состояния покоя и через 15 с его угловая скорость достигла 30 рад/с. С этой угловой скоростью тело вращалось 10 с равномерно, а затем стало вращаться равнозамедленно в течение 5 с до полной остановки.
1) число оборотов и среднюю угловую скорость тела за все время вращения;
2) окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения тела через 5 с после начала движения.
Решение
1. Разграничим вращательное движение данного тела на участки равноускоренного, равномерного и равнозамедленного движения. Определим параметры вращательного движения тела по этим участкам.
2. Равноускоренное вращение (участок 1):
3. Равномерное вращение (участок II):
4. Равнозамедленное вращение (участок III):
5. Определим полное число оборотов тела за все время вращения:
6. Определим среднюю угловую скорость тела за все время вращения:
7. Определим окружную скорость точек тела, расположенных на расстоянии r = 0,5 м от оси вращения через 5 с после начала движения тела:
Пример 8. Диск радиусом R = 2 м вращается вокруг неподвижной оси согласно уравнению
(φ — в радианах, t — в секундах). Определить скорость и ускорение точки поверхности диска в моменты времени t1 = 0 и t2 = 2 с.
Решение
Для определения скорости и ускорения точки необходимо знать угловую скорость и угловое ускорение диска.
Уравнение изменения угловой скорости диска:
Уравнение изменения углового ускорения диска:
Определим угловую скорость и угловое ускорение диска в моменты времени t1 = 0 и t2 = 2 с:
Определим скорость точки поверхности диска в указанные моменты времени:
Определим нормальное и касательное ускорения точки поверхности диска в моменты времениt1 и t2:
Пример 9. Точка А, лежащая на ободе равномерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускорением ап = 5 м/с 2 . Определить радиус шкива OA и величину угловой скорости (рис. 1.46).
Решение
Здесь для решения следует воспользоваться известными соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:
Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:
Пример 10. Шарик А (рис. 1.47), подвешенный на стержне OA, колеблется в вертикальной плоскости около неподвижной горизонтальной оси О согласно уравнению
(φ — в радианах, t — в секундах).
1. Ближайшие моменты времени, соответствующие максимальным отклонениям стержня OA от вертикали OC вправо и влево, а также значение максимальных углов отклонения.
2. Ближайший момент времени после начала движения, при котором нормальное ускорение шарика равно нулю.
3. Ближайший момент времени, при котором касательное ускорение шарика равно нулю.
4. Полное ускорение шарика при t = 1,5 с и угол, образованный вектором ускорения со стержнем OA.
Решение
Стержень OA совершает вращательное (колебательное) движение. Максимальные углы отклонения стержня от вертикали соответствуют наибольшим абсолютным значениям функции sin (πt/6). Очевидно, это имеет место при sin (πt/6) = ± 1:
Крайние положения стержня OA на рис. 1.47 показаны штриховыми линиями OA1 и ОА2.
Напомним, что за положительное направление считаем вращение по часовой стрелке.
Уравнение изменения угловой скорости стержня OA
Уравнение изменения углового ускорения стержня OA
Направления ω и ε показаны на рис. 1.47. В приведенном примере направления ω и ε противоположны. Следовательно, стержень OA совершает замедленное вращательное движение.
Нормальное и касательное ускорения шарика определяются по формулам:
В рассматриваемом примере касательное ускорение шарика направлено к точке С (рис. 1.47).
Определим момент времени, при котором ап равно нулю. Для этого выражение ап приравняем нулю:
Записанное условие выполняется при
Нормальное ускорение шарика равно нулю, когда стержень OA занимает крайние положения.
Определим момент времени, при котором at равно нулю. Для этого выражение at приравняем нулю:
Это условие выполняется при
 |
Касательное ускорение шарика обращается в ноль в тот момент, когда стержень OA совпадает с линией OC. Вычислим аn и at при t = 1,5 с:
Ускорение шарика при t = 1,5 с
Угол между вектором ускорения шарика и стержнем OA определяется из соотношения
Пример 11. Через 30 с равномерного вращательного движения с частотой n0 = 600 об/мин тело начало равнозамедленное движение и в течение последующих 20 с частота вращения тела уменьшилась до n = 450 об/мин.
Определить угловое ускорение тела при равнозамедленном вращательном движении, а также количество оборотов тела за время равномерного и равнозамедленного движения.
Решение
1. Переведем начальную и конечную частоты вращения тела в единицы угловой скорости:
2. За время t1 = 30 с тело, вращаясь равномерно с угловой скоростью ω0 = 20π рад/с, повернулось на угол
3. По формуле угловое ускорение, с которым тело вращалось в течение времени t2 = 20 с
4. За время равнозамедленного движения тело повернулось на угол
5. За весь промежуток времени t1 + t2 = 50 с тело повернулось на угол
следовательно, тело сделало
Для определения количества оборотов, сделанных телом, можно было частоту вращения и не переводить в единицы угловой скорости. За время t1 = 30 с = 0,5 мин при равномерном движении тело сделало
За время t2 = 20 с = 1/3 мин при равнозамедленном вращении тело сделало
Контрольные вопросы и задания
1. Какими кинематическими параметрами характеризуется поступательное движение и почему?
2. Запишите уравнение равномерного поступательного движения твердого тела.
3. Запишите уравнение равнопеременного поступательного движения твердого тела.
4. Запишите уравнения равномерного и равнопеременного вращательного движений твердого тела.
5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение?
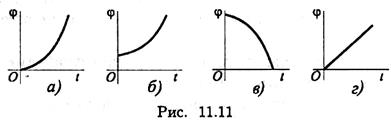
6. Для заданного закона (уравнения) движения
φ = 6,28 + 12t + 3t 2 выберите соответствующий кинематический график движения (рис. 11.11).
7. Для движения, закон которого задан в вопросе 6, определите угловое ускорение в момент t = 5 с.
Видео:Как регулируется скорость вращения ротора асинхронных электродвигателей.Скачать
Примеры решения задач
Пример 1. Ротор электродвигателя вращается со скоростью, описываемой уравнением
Определить вид движения.
Решение
1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение — постоянно, ε = ω’ = 2π = const.
2. Движение равнопеременное (равноускоренное, т.к. ускорение положительно).
Пример 2 Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение.
Решение
1. Один оборот равен 2π радиан. Следовательно:
360 оборотов = 720π рад, φ = 720π рад.
2.
 |
Закон равнопеременного вращательного движения
Пример 3. Тело вращалось с угловой частотой 1200 об/мин. Затем движение стало равнозамедленным, и за 30 секунд скорость упала до 900 об/мин. Определить число оборотов тела за это время и время до полной остановки. Использовать пункт 1 примера 3.
Решение
1. Построить график изменения скорости за 30 с (рис. 11.9).
 |
Определяем угловую скорость вращения тела:
Определяем угловое ускорение:
Определяем угол поворота за прошедшее время:
Число оборотов за 30 с:
2. Определяем время до полной остановки.
Скорость при остановке равна нулю, ω = 0.
Пример 5. Маховое колесо вращается равномерно со скоростью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить скорость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.
Решение
 |
Касательное ускорение точки A atA = 0; нормальное ускорение точки А аnA = ω 2 rA
апA = (12,56) 2 • 0,3 = 47,3м/с 2 . 5. Полное ускорение точек на ободе колеса
Пример 9. Точка А, лежащая на ободе равномерно вращающегося шкива, движется со скоростью v = 2 м/с и нормальным ускорением ап = 5 м/с 2 . Определить радиус шкива OA и величину угловой скорости (рис. 1.46).
Решение
Здесь для решения следует воспользоваться известными соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:
Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:
Контрольные вопросы и задания
1. Какими кинематическими параметрами характеризуется поступательное движение и почему?
2. Запишите уравнение равномерного поступательного движения твердого тела.
3. Запишите уравнение равнопеременного поступательного движения твердого тела.
4. Запишите уравнения равномерного и равнопеременного вращательного движений твердого тела.
5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение?
6. Для заданного закона (уравнения) движения
φ = 6,28 + 12t + 3t 2 выберите соответствующий кинематический график движения (рис. 11.11).
Дата добавления: 2017-09-01 ; просмотров: 6372 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Как определить скорость вращения вала электродвигателя и его мощность.Скачать
Лексические нормы (стр. 9 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Определить вид движения
2. Закон вращательного движения колеса ц = 0,3t3 + 3.
Определить ускорение колеса в момент t = 5 с
3. При торможении ротора электродвигателя его скорость меняется согласно графику.
Рассчитать число оборотов ротора до полной остановки
4. Какие ускорения возникнут в точке А при равномерном вращении колеса?
5. Определить полное ускорение на ободе колеса r= 0,6 м, при t = 3 с, если щ = 11 рад/с. Движение равномерное
Тест №12 КИНЕМАТИКА вариант 4
1. По заданному закону вращения регулятора
Определить вид движения
2. Закон вращательного движения 3колеса
Определить время до полной остановки
3. По условию предыдущей задачи определить число оборотов колеса до остановки
4. При вращении скорость маховика изменяется по графику.
Определить угловое ускорение маховика в конце рассматриваемого участка
n1= 420 об/мин, t1 = 20 с
5. Определить нормальное ускорение точек на ободе колеса диаметром 0,2 м, если закон движения
Тест № 12 КИНЕМАТИКА вариант 5
1. Закон движения колеса
Определить угловую скорость вращения колеса в момент t = 5 с
2. Колесо вращается по закону, приведенному в вопросе 1. Определить угловое ускорение колеса в момент t= 3 с
3. Скорость ротора менялась согласно графику и за 120 оборотов достигла щ= 50,2 рад/с.
Определить время разгона до указанной скорости
3. При вращении колеса скорость и ускорение в точке А имеют указанные на чертеже направления. Определить вид вращения, если
5. Колесо вращается с частотой п = 250 об/мин. Определить полное ускорение точек на ободе колеса r=0,8м
Ответы к тесту №12:
Сложное движение точки.
В мире все находится в непрерывном движении, и неподвижная система координат в действительности не существует. Поэтому возникает необходимость рассматривать движение точек одновременно по отношению к двум системам отсчета, одна из которых считается неподвижной, а вторая определенным образом движется по отношению к первой. Движение точки в данном случае называется сложным.
Движение точки по отношению к неподвижной системе координат называется абсолютным. Движение точки по отношению к подвижной системе координат называется относительным. Движение подвижной системы координат по отношению к неподвижной называется переносным. Абсолютное движение является сложным и состоит из относительного и переносного движений.
В тех случаях, когда заданы движения двух или более тел (точек) относительно неподвижной системы координат и необходимо определить движение одного из этих тел относительно другого, удобно пользоваться расчленением абсолютного движения на переносное и относительное.
Тело, относительно которого требуется рассмотреть движение, мысленно остановим, а неподвижную систему координат заставим двигаться по его закону, но в обратном направлении. Тогда для второго тела это движение станет переносным, а движение второго тела — относительным. После этого просто понять, как будет двигаться второе тело по отношению к первому.
При изучении сложного движения точки будем рассматривать только перемещение и скорость.
Если переносное и относительное движения направлены вдоль одной прямой, то
перемещение точки в абсолютном движении равно алгебраической сумме перемещений в переносном и относительном движениях.; скорость точки в абсолютном движении равна алгебраической сумме переносной и относительной скоростей.
Условимся направление переносного перемещения и соответственно направление переносной скорости считать положительными. Тогда относительное перемещение и соответственно относительная скорость будут также положительными, если они направлены в ту же сторону, что и переносное. Если же относительное перемещение имеют направление, противоположное переносному, то будем считать их отрицательными.
Таким образом, при совпадении направлений переносного и относительного движений 
При противоположных друг другу направлениях переносного и относительного движений 
Модуль абсолютной скорости находится по теореме косинусов:
, а направление по теореме синусов
Указания к решению задач:
Выяснить, какое движение является абсолютным, какое относительным, какое переносным. Направить векторы абсолютной, относительной и переносной скоростей. Простроить параллелограмм или треугольник скоростей и из него найти неизвестные величины.
Наклонная плоскость АВ (рис.6) с углом ВАС, равным 450, движется прямолинейно с постоянной скоростью v=5 м/с. По плоскости скользит тело G со скоростью 2t. определить абсолютную скорость тела через 5 с после начала движения, считая, что в начальный момент относительная скорость тела G равнялась нулю.
🎦 Видео
Урок 89 (осн). Задачи на вращательное движение - 1Скачать
К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать
Поступательное и вращательное движенияСкачать
Физика - движение по окружностиСкачать
Ременная передача. Урок №3Скачать
Определение скорости и ускорения при поступательном и вращательном движении.Скачать
Урок 50. Задачи на вращение с пост. угловым ускорениемСкачать
Как рассчитать диаметр шкивов и линейную скорость?Скачать
Регулирование частоты вращения ротора трехфазных асинхронных двигателейСкачать
решение задач кинематики и динамики часть3Скачать
РОТОР НЕ ВСЕГДА ЯКОРЬ или "маленький ликбез благодаря википедической премудрости"Скачать
Как изменить направление вращения трехфазного асинхронного двигателя?Скачать
Динамическое торможение. Как мгновенно остановить асинхронный двигатель?Скачать
Управление скоростью вращения двигателяСкачать
Включение асинхронного электродвигателя с нужным направлением вращения валаСкачать
Разновидность неисправности якоря коллекторного мотора. Упали обороты и пошел запах.Скачать
прямолинейное РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ | формулы кинематикиСкачать
Проблема с ротором электродвигателя.Скачать
