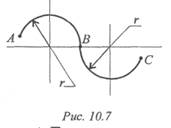
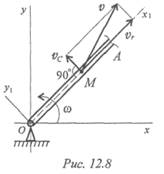
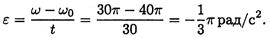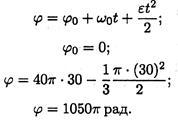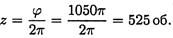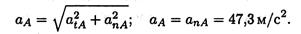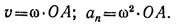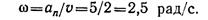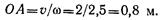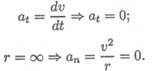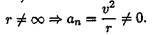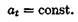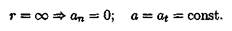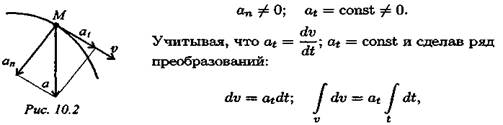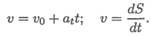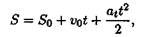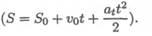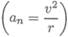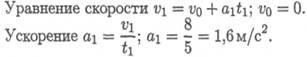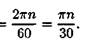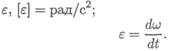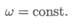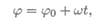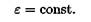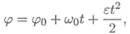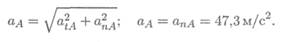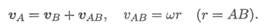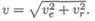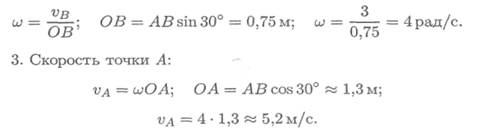Пример 1. Ротор электродвигателя вращается со скоростью, описываемой уравнением
Определить вид движения.
Решение
1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение — постоянно, ε = ω’ = 2π = const.
2. Движение равнопеременное (равноускоренное, т.к. ускорение положительно).
Пример 2 Тело вращалось равноускорено из состояния покоя и сделало 360 оборотов за 2 мин. Определить угловое ускорение.
Решение
1. Один оборот равен 2π радиан. Следовательно:
360 оборотов = 720π рад, φ = 720π рад.
2.
 |
Закон равнопеременного вращательного движения
Пример 3. Тело вращалось с угловой частотой 1200 об/мин. Затем движение стало равнозамедленным, и за 30 секунд скорость упала до 900 об/мин. Определить число оборотов тела за это время и время до полной остановки. Использовать пункт 1 примера 3.
Решение
1. Построить график изменения скорости за 30 с (рис. 11.9).
 |
Определяем угловую скорость вращения тела:
Определяем угловое ускорение:
Определяем угол поворота за прошедшее время:
Число оборотов за 30 с:
2. Определяем время до полной остановки.
Скорость при остановке равна нулю, ω = 0.
Пример 5. Маховое колесо вращается равномерно со скоростью 120 об/мин (рис. 11.10). Радиус колеса 0,3 м. Определить скорость и полное ускорение точек на ободе колеса, а также скорость точки, находящейся на расстоянии 0,15 м от центра.
Решение
 |
Касательное ускорение точки A atA = 0; нормальное ускорение точки А аnA = ω 2 rA
апA = (12,56) 2 • 0,3 = 47,3м/с 2 . 5. Полное ускорение точек на ободе колеса

Решение
Здесь для решения следует воспользоваться известными соотношениями для линейной скорости и нормального ускорения точек вращающегося тела:
Если второе уравнение разделить на первое, найдем угловую скорость вращения шкива:
Контрольные вопросы и задания
1. Какими кинематическими параметрами характеризуется поступательное движение и почему?
2. Запишите уравнение равномерного поступательного движения твердого тела.
3. Запишите уравнение равнопеременного поступательного движения твердого тела.
4. Запишите уравнения равномерного и равнопеременного вращательного движений твердого тела.
5. Задано уравнение движения тела S = f(t). Как определяют скорость и ускорение?
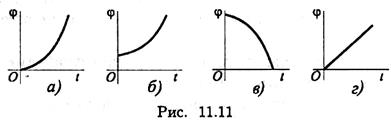
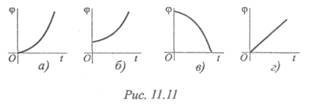
6. Для заданного закона (уравнения) движения
φ = 6,28 + 12t + 3t 2 выберите соответствующий кинематический график движения (рис. 11.11).
Дата добавления: 2017-09-01 ; просмотров: 6389 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Как регулируется скорость вращения ротора асинхронных электродвигателей.Скачать

Ротор электродвигателя вращается со скоростью описываемой уравнением
Как и всякая наука, математика имеет свою историю, подчас не менее интересную, чем история войн, государств, великих личностей. На протяжении тысячелетий – от зари человечества, когда первые математические символы – числа только появлялись и имели причудливую, непонятную для нынешнего человека форму до современности, эпохи компьютеров, работающих на основе математических законов – формировалась математическая наука. Подобно географическим открытиям, расширяющим знания человека о мире, и математика открывала для человека новые горизонты: люди учились измерять, считать окружающий их мир, задумываться о закономерностях того или иного природного явления и находить вокруг себя гармонию. Основные математические понятия позволяют глубже осмысливать и анализировать различные факты, видеть их общие черты и различия, формулировать мысли и делать выводы.
И если эпоха Великих географических открытий имеет чётко очерченные исторические рамки, то эпоха математических открытий, похоже, не закончится никогда. Область применения математики не ограничена: все виды движения материи могут изучаться математически.
Изучение математики развивает логическое мышление, приучает человека к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека.
Актуальность моего исследования состоит в том, что несмотря на частые высказывания: «Зачем нужно изучать математику, решать задачи? Научились считать, этого достаточно», нужно учитывать тот факт, что при подготовке техников в колледже курс математики решает задачу математического обеспечения специальной подготовки, то есть выработки умений по математике (общих и профессиональных компетенций), необходимых для изучения общетехнических и специальных дисциплин, разработки курсовых и дипломных проектов, использования в профессиональной деятельности.
После первого урока математики в домашнем сочинении «Математика в жизни и будущей профессии» мы смогли написать только общие фразы. В процессе первого года учебы в колледже размышления о важности математики подтолкнули к работе над данной темой.
обоснование необходимости изучения математики для овладения знаниями по специальности «Автомеханик».
изучить в каких областях математические знания более востребованы;
отобрать задачи, связанные с профессией автомеханика,
доказать важность владения математическими знаниями, обеспечивающими успешность, благополучие в профессиональной деятельности.
Объект исследования: профессия автомеханика.
Предмет исследования: применение математического аппарата в общетехнических дисциплинах при обучении специальности 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта.
поиск информации о применении математики в профессии автомеханика из различных источников;
работа с задачами из курса математики и других дисциплин.
Практическая значимость работы состоит в том, что материалы будут полезны обучающимся специальностей технического профиля для повышения уровня математической компетентности. Преподаватели математики могут использовать приведенные в работе задания для вооружения обучающихся знаниями и умениями, необходимыми для решения профессиональных задач с использованием математических методов. Преподаватели других дисциплин могут использовать работу, чтобы воспитать у обучающихся потребность в совершенствовании знаний в области математики и ее приложений.
Кто такой «автомеханик»?
Автомеханик – это рабочий широкого профиля, который выполняет операции по техническому обслуживанию и ремонту автотранспортных средств, контролирует техническое состояние автомобилей с помощью диагностического оборудования и приборов, управляет автотранспортными средствами.
Можно сказать, что профессия автомеханикапоявилась в XVIII веке, ведь именно в это время в разных странах мира появились первые самоходные коляски – транспорт, способный передвигаться самостоятельно. В течение длительного времени самодвижущиеся механизмы видоизменялись и совершенствовались. Но, как всякий механизм, они требовали ухода и ремонта в случае поломки. Этим могли заниматься только люди, хорошо разбирающиеся во внутреннем устройстве автомобиля. Так появилась новая профессия – автомеханик или автослесарь. Эта профессия позволяет увеличивать сроки эксплуатации автомобиля, осуществлять своевременную профилактику его функционального состояния, что обеспечивает безопасность дорожного движения.
Виды деятельности профессии автомеханика
— Установление технического диагноза путем внешнего осмотра и инструментального контроля.
— Своевременное и качественное проведение технического обслуживания автомобиля.
— Осуществление ремонта автомобиля и его деталей.
— Проведение технического осмотра, сборки, разборки, ремонта, замены всех соединений, узлов и электрооборудования автомобилей.
— Регулирование механизмов и замена при необходимости неисправных деталей.
— Проверка и испытание исправности деталей и узлов автомобиля.
— Поддержание в технически исправном, пригодном для эксплуатации состоянии автомобиля, его агрегатов, систем и механизмов.
Человек, работающий автомехаником, должен иметь такие способности, личностные качества, интересы и склонности, которые указаны в таблице:
Личностные качества, интересы и склонности
— концентрация внимания (способность в течение длительного времени заниматься определенным видом деятельности);
— высокий уровень устойчивости внимания;
— хорошее пространственное воображение;
— хорошая моторная память (память на действия);
— физическая сила и выносливость;
— развитая ручная моторика;
— хорошая координация движений;
— эмоциональная стабильность и надежность;
— ответственность за выполняемую работу;
— тщательность, аккуратность, систематичность в работе;
Область машины, где пригодятся знания по математике
1. Для того, чтобы зеркало фар отражало лучи параллельным пучком, зеркалу нужно придать форму параболоида вращения, внутри которого в определенной точке (в фокусе) находится лампочка. Параболоид вращения – это поверхность, которая образуется при вращении параболы вокруг ее оси. В курсе алгебры мы изучали эту тему «График функции y=x 2 ».
2. Чтобы изготовить шестеренку надо окружность разделить на n равных частей. С этой задачей мы встречались на уроках геометрии: научились при помощи циркуля, линейки и транспортира делить окружность на любое количество равных частей.
3. Для подбора поршней к цилиндрам вычисляют зазор между ними. Зазор определяется как разность между замеренными диаметрами поршня и цилиндра. Номинальный зазор равен 0,025-0,045 мм, предельно допустимый – 0,15 мм. Диаметр поршня измеряют микрометром в плоскости, перпендикулярной оси поршневого пальца, на расстоянии 51,5 мм от днища поршня.
4. Пуск двигателя и установка колеса прямо. Слегка повернуть рулевое колесо в одну и другую сторону. В случае, если люфт составляет более 30 мм, необходимо проверить рулевое управление и все детали рулевого механизма на чрезмерный люфт. На легковом автомобиле люфт не должен превышать 10 градусов, на грузовом — 25 градусов, на автобусе — 20 градусов.
5. Умение математически грамотно прочитать таблицу.
Задачи, решаемые в профессиональной деятельности
1. Расчет остановочного пути
Выбирая скорость движения, водитель должен всегда помнить, что остановить автомобиль в один миг невозможно. Остановочный путь – это расстояние, пройденное транспортным средством с момента обнаружения водителем опасности до полной остановки. Состоит он из двух отрезков – это путь, проехавший автомобилем за время реакции водителя и тормозного пути, плюс зависимость от состояния дороги и многих других факторов.
Задача.Легковой автомобиль движется по сухой дороге со скоростью 40 км/час. Тормозной путь легкового автомобиля при этой скорости составляет 14,7 м. Какую длину составит остановочный путь, если реакция водителя составляет 1сек?
Решение: 40 км = 40000м; 1час = 3600сек
1) 40000:3600=11(м) – путь, пройденный автомобилем за время 1 с реакции водителя.
2) 11 + 14,7 = 25,7(м) – длина остановочного пути.
2. Текстовые задачи на движение
1) Два грузовика выехали в рейс по взаимно-перпендикулярным дорогам. Скорость одного – 50 км/ч, скорость другого – 60 км/ч, в данный момент они находятся на расстоянии 7 км и 10 км от начала пути. Через какое время расстояние между ними будет 35 км?
2) Расстояние от Перми до Казани, равное 723км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723 км) расстояние, пройденное за первые 9 часов движения
723-55*9= 723-495=228 (км).
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
Ответ: скорость автомобиля в оставшееся время составила 57 км/ч.
3. Задачи на расчет различных элементов работы автомобиля
1) Во время загородной поездки автомобиль на каждые 100 км пути расходует на 2 л бензина меньше, чем в городе. Водитель выехал с полным баком, проехал 120 км по городу и 210 км по загородному шоссе до заправки. Заправив машину, он обнаружил, что в бак вошло 42 л бензина. Сколько литров бензина расходует автомобиль на 100 км пробега в городе?
Из задачи следует, что на маршрут в 120 км по городу и 210 км по загородному шоссе было израсходовано 42 литра бензина. Обозначим через x л – расход бензина на 100 км в городе. Соответственно, расход вне города составит (х-2) л на 100 км. Тогда расход бензина в городе на 120 км составит 120х/100 л, а по загородному шоссе, длинной 210 км – 210(х-2)/100 л. В сумме расход составил 42 л, имеем:
330х=4620, х=14 (л) – автомобиль расходует в городе на 100 км пути.
2) Автомобилист отправился в путешествие и первую остановку сделал через 580 км, а вторую через 420 км после первой остановки. При этом было истрачено по 7 л бензина на каждые 100 км пути. Сколько топлива было потрачено?
Найдём всё расстояние, которое проехал автомобиль
580 км + 420 км =1000 км.
Расход топлива рассчитывают из расчёта на 100 километров. Поэтому найдём «сколько раз по 100» проехал автомобиль
1000 км : 100 км = 10.
Поскольку расход бензина 7 л на 100 км, то всего было израсходовано 10*7 = 70 л бензина.
3) Сколько брезента необходимо для пошива тента для кузова машины формы прямоугольного параллелепипеда – имеющего размеры: 3м*1,5м*2 м?
4) Хватит ли 20 м арматуры для изготовления каркаса кузова для Камаза, имеющего форму прямоугольного параллелепипеда с измерениями: 2м*1,5м*2м?
5) Куча щебня имеет форму конуса, радиус основания которого 20 м, а образующая 70 м. Сколько потребуется таких куч щебня, чтобы загрузить БЕЛАЗ грузоподъёмностью 40 т ? Плотность щебня 1300 кг/м 3 .
6 ) На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. В какой момент времени двигатель разогрелся максимально?
7) Плотность электролита полностью заряженной АКБ – 1.27 г/см 3 . При очередном ТО-2 показания амперметра – 1,22 г/см 3 . На сколько % разрядилась батарея и допускается ли ее эксплуатация в зимнее время?
8) Найдите объект камеры сгорания двигателя автомобиля ЗИЛ-130, если диаметр поршня 100 мм, ход поршня 150 мм (без учёта головки блока).
9) Определить ёмкость масляного бака насоса гидроусилителя автомобиля ЗИЛ-130, если его диаметр 126 мм, высота 140 мм.?
10) Реакция водителя не должна превышать – 1 сек. Какое расстояние пройдет автомобиль за 1 секунду при υ= 80 км/ч. Определить безопасную дистанцию при υ= 90 км/ч.
4. Задачи на проценты
1) Бензин стоил 35 рублей за 1 литр. Сначала его стоимость повысили на несколько процентов. Потом стоимость повысили ещё на такое же количество процентов. После этого стоимость бензина стала 42,35 рубля за 1 литр. На сколько процентов повышали цену бензина каждый раз?
Обозначим за х – коэффициент увеличения цены на бензин. Тогда после первого увеличения цены бензин стал стоить (35*х) рублей. А после второго увеличения цена бензина за один литр составила х*(35*х)рублей.
35х² = 42,35 рублей,
Поскольку каждый раз цена бензина увеличивалась в 1,1 раза, то значит увеличение цены каждый раз составляло 10%.
2) Машина с прицепом может перевезти 12 тонн груза. Сколько груза вмещает прицеп, если машина вмещает 60% груза?
12 т = 100%, 12000/100*60 = 7200кг – уходит груза в машину;
12000 – 7200 = 4800кг – уходит груза в прицеп;
3) Автомобильный завод в первый месяц выпустил 160 автомобилей. В следующем месяце завод автомобилей увеличил выпуск этих автомобилей на 200%. Во сколько раз увеличился выпуск автомобилей? Сколько автомобилей стал выпускать завод?
Исходный выпуск автомобилей составляет 100%, т.е. 160 автомобилей – это 100%. Тогда в следующем месяце выпуск автомобилей составил 100% + 200% = 300%, т.е. в 3 раза больше. Значит, завод стал выпускать 160*3=480 автомобилей.
Ответ: в 3 раза, 480 автомобилей.
4) Автомеханик установил сначала 25% всех деталей машины при ремонте, потом 70% оставшихся деталей. После этого осталось ещё установить 27 деталей. Сколько всего деталей нужно было установить автомеханику?
5. Задачи на вероятность
1) Два автомобилиста, независимо друг от друга, выезжают из пункта А в пункт В. Навигатор предлагает каждому из них 8 равноценных маршрутов, и автомобилисты выбираю маршрут случайным образом. Найдите вероятность того, что автомобилисты выберут различные маршруты.
Первый автомобилист случайным образом выберет один маршрут из восьми. Тогда, чтобы второй выбрал другой маршрут (не совпадающий с первым) он должен случайно попасть на один из 7 оставшихся. Получаем число благоприятных исходов m = 7, общее число исходов n = 8 и значение искомой вероятности: P = m / n = 7/8 = 0,875
2) Автомобильные номера состоят из трёх букв (в современных номерах используется 12 букв) и трёх цифр (используются все 10 цифр). Сколько автомобилей можно занумеровать таким образом в пределах одного региона, чтобы никакие два автомобиля не имели одинаковые номера?
На первом месте у автомобильного номера может быть любая из 12 букв. Следовательно, первая буква может быть выбрана 12 способами. На втором месте также может находиться любая из 12 букв, поэтому первые две буквы номера могут быть выбраны 12 2 способами. Ясно, что три буквы можно выбрать 12 3 способами. Аналогично рассуждая, получаем, что три цифры можно выбрать 10 3 -1=999 способами. Таким образом, всего может быть занумеровано 12 3 · 999 = 1 728 272 автомобилей
Ответ: 1 728 272.
3) В ящике в случайном порядке разложены 25 деталей, причем 5 из них стандартные. Рабочий берет наугад 5 деталей. Найдите вероятность того, что из взятых наугад деталей 3 окажутся стандартными.
6. Задачи из электротехники
Казалось бы зачем электротехника слесарю механосборочных работ или строителю, станочнику широкого профиля или технологу, механику или автослесарю? А разве слесарь не использует в своей производственной деятельности, например, электродрель? Чтобы стать хорошим специалистом в своей области и к тому же не получить «удар в спину» от «обиженной» электроустановки, необходимо знать основные законы, которые положены в основу работы самых различных электротехнических устройств, представлять их конструкцию, принцип действия, основные характеристики, методы испытаний, области применений и, наконец, алгоритмы их расчёта.
Электротехника – это наука об основных законах физики в области электричества и его применении в промышленности и быту.
1) В электрической цепи постоянного тока (рис.2) амперметр А показывает I5 = 5А. Методом уравнений Кирхгофа рассчитать токи I1, I2, I3, I4 в ветвях цепи. Сопротивления резисторов: R1 = 1 Ом; R2 = 10 Ом; R3 = 10 Ом; R4 = 4 Ом; R5 = 3 Ом; R6 = 1 Ом; R7 = 1 Ом; R8 = 6 Ом; R9 = 7 Ом. Величины ЭДС: E1 = 162В; E2 = 50В; E3 = 30В. Внутренними сопротивлениями источников питания пренебречь. Решить задачу для случая, когда показание амперметра неизвестно.
Решение: При заданном включении источников питания за положительные направления токов принимаем направления, указанные на схеме рис. 2. В схеме – 3 узла и 5 ветвей, следовательно, необходимо определить 5 неизвестных токов. В соответствии с этим составляют два уравнения по 1 закону Кирхгофа и три – по 2 закону Кирхгофа.
Для узлов 1и 2цепи составляют уравнения для токов по 1 закону Кирхгофа:
По 2 закону Кирхгофа уравнение для левого контура с ЭДС E1 и E2:
Для правого контура с амперметром А в ветви:
Ток в цепи резистора R4 определяют из последнего уравнения:
Ток I3 в ветви резистора R3 находят из уравнения, составленного для узла 2цепи: I3 = I4 + I5 = 7А.
Ток в ветви резистора R2 находят из уравнения, записанного для среднего замкнутого контура: E 2 – E 3 = –10 I 2 + 10·7 + (4 + 6)·2, откуда I 2 = 7 A .
Ток в ветви с резисторами R1, R6, R7 находят из уравнения:
Ток I1 можно также определить из уравнения
Если ток в ветви резисторов R5 и R9 не задан, то искомые токи и их направления в других ветвях определяют, решая систему пяти уравнений, составленных по законам Кирхгофа. Положительные значения токов свидетельствуют о том, что действительные направления токов в соответствующих ветвях совпадают с условными направлениями.
2) Двигатель постоянного тока ДПМ – 25 – Н3 – 16 с возбуждением от постоянных магнитов, имеющий nном=5200об/мин; Uном=27В; Iном=0,5А; Rя+ R щ=0,5Ом, используется в качестве тахогенератора для контроля за частотой вращения асинхронного двигателя. Определить ожидаемую ЭДС на щётках машины при частоте вращения асинхронного двигателя n =2970 об/мин.
Определяем против ЭДС при работе машины в режиме двигателя:
Эта ЭДС возникает в двигателе при номинальном напряжении и номинальной частоте вращения. Поскольку Е=СеФв n , можно вычислить коэффициент пропорциональности k=СеФв=Е/n=26,75/5200=0,005. Этот коэффициент остаётся тем же самым при работе машины в режиме генератора. Действительно, коэффициент Се определяется конструкцией машины, а поток Ф – магнитными характеристиками статора. Оба эти параметра остаются неизменными при работе и в режиме генератора, и в режиме двигателя.
Следовательно, при работе двигателя в режиме тахогенератора ротор которого приводится в действие асинхронным двигателем, ожидаемая ЭДС на щётках Е = СеФв n = kn = 0,005·2970 = 14,85В.
Ответ: При работе двигателя в качестве тахогенератора совместно с асинхронным двигателем ожидаемая ЭДС равна 14,85В.
7. Задачи из технической механики
Автомеханик должен знать техническую механику, этот предмет ему нужен и необходим в его профессии.
Техническая механика – это наука об общих законах механического движения и применения их в современной технике.
Техническая механика состоит из двух частей: теоретической и прикладной. Первая часть посвящена изучению теоретических основ механического движения, вторая – использованию положений теоретической механики для практических целей: проектирования механизмов, расчета деталей машин, строительных конструкций и сооружений.
Достижения технической механики позволяют не только улучшать конструкции машин и механизмов, но и совершенствовать производственные процессы. Сегодня на многих предприятиях широко используются машины-автоматы, автоматические поточные линии, которые без прямого участия человека обеспечивают выпуск готовой продукции, начиная с обработки сырья и кончая упаковкой готовых изделий.
1)Ротор электродвигателя вращается со скоростью, описываемой уравнением ω = 2π t . Определить вид движения.
1. Анализируем выражение для скорости: скорость меняется и зависит от времени линейно. Следовательно, угловое ускорение – постоянно, ε = ω’ = 2π+ const .
2. Движение равнопеременное (равноускоренное, т.к ускорение положительно).
2) Тело вращалось равноускоренно из состояния покоя и сделало 360 оборотов за 2 минуты. Определить угловое ускорение.
1 оборот = 2π радиан. Следовательно: 360 оборотов = 720π рад, φ = 720π рад.
2. Закон равнопеременного вращательного движения: φ = φ0 + ω0 t +
В данном случае φ0 = 0; ω0 = 0. Следовательно, φ = . Откуда ε = .
Угловое ускорение равно ε = = 0,314 (рад/с 2 )
Ответ: 0,314 рад/с 2 .
3) Определить работу силы тяжести при перемещении груза из точки А в точку С по наклонной плоскости (рис.3). Сила тяжести тела 1500Н. АВ=6м, ВС=4м.
1. Работа силы тяжести зависит только от изменения высоты груза. Изменение высоты при перемещении из точки А в С:
2. Работа силы тяжести А = F т∆h = 1500 · 0,2 = 300 (Дж).
4) По заданному графику угловой скорости (рис.4) определить вид вращательного движения.
1. Участок 1 – неравномерное ускоренное движение, ω = φ’; ε = ω’.
2. Участок 2 – скорость постоянна – движение равномерное, ω = const.
3. Участок 3 – скорость убывает равномерно – равнозамедленное движение,
ε = ω ‘ t . Конечная скорость υ = 0 ( остановка).
R = G = mg, здесь R— сила прижатия; f — коэффициент трения; G – сила тяжести; m – масса автомобиля; g – ускорение свободного падения, 9,81 м/с 2 .
3. После подстановок получаем формулу для определении времени торможения.
В ходе выполнения данной работы мы убедились, что применение математики можно найти в любой сфере деятельности человека. Математика – это феномен общемировой культуры, в ней отражена история развития человеческой мысли. Задачи по математике развивают логическое, творческое и аналитическое мышление, формируют научные познания об основных понятиях математического анализа, навыки поиска рациональных путей решения, помогают принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
Известный голландский математик Г. Фройдейталь (1905-1990) утверждал: «Важно, чтобы изучаемая математика была тесно связана с реальной действительностью, только так можно обеспечить длительное влияние математики на обучающегося». Каждому человеку в своей жизни, в том числе и мне, приходится выполнять достаточно сложные расчеты, пользоваться вычислительной техникой, находить и применять нужные формулы, владеть приемами геометрических измерений, читать информацию, представленную в виде схем, таблиц, графиков и диаграмм.
Именно такая цель о применении математического аппарата при изучении отдельных разделов общетехнических дисциплин ставилась в начале работы, и она достигнута. Запланированная совместная работа с преподавателями общетехнических дисциплин по отбору и систематизации материала для данной работы обеспечила решение поставленных задач.
Осуществление междисциплинарных связей изучаемых дисциплин, профессиональная направленность математической подготовки в технических образовательных учреждениях обеспечивает повышение уровня математической компетентности обучающихся, помогает осознанию ценности математики для будущей профессиональной деятельности, развивает профессионально значимые качества и приемы умственной деятельности.
Проведя анализ, я выяснил в каких областях автомобиля, в работе автомеханика могут использоваться и понадобятся знания математики. В ходе работы над проектом я сделал вывод о том, что «Математика» нужна не только в моей будущей профессии техника-механика, математика нужна всем людям на земле. Она позволяет человеку думать. Для технических профессий всегда необходимы задачи на движение, проценты, площади и объемы, составление уравнений и систем уравнений.
Автомеханик должен постоянно совершенствовать свои профессиональные навыки и знания рынка автомобилей. Следить за всеми новшествами и передовыми технологиями в мировом автомобилестроении. Если вы удачно выбрали профессию и вложите в неё душу, то счастье само вас отыщет.
1. А. И Аркуша. Техническая механика, 2005.
2. И.О. Мартынова. Электротехника, 2015.
3. М.С.Мовнин, А.Б.Израелит, А.Г.Рубашкин. Основы технической механики, 2005.
Видео:Ременная передача. Урок №3Скачать

Ротор электродвигателя вращается со скоростью описываемой уравнением
параметров движений
Равномерное движение
Равномерное движение — это движение с постоянной скоростью:
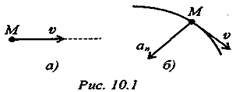
Для прямолинейного равномерного движения (рис. 10.1а)
Полное ускорение движения точки равно нулю: а = 0.
При криволинейном равномерном движении (рис. 10.16)
Полное ускорение равно нормальному ускорению: а = ап.
Уравнение (закон) движения точки при равномерном движении можно получить, проделав ряд несложных операций.
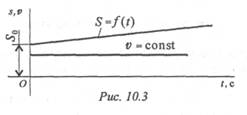
Так как v = const, закон равномерного движения в общем виде является уравнением прямой: S = So + vt , где So — путь, пройденный до начала отсчета.
Равнопеременное движение
Равнопеременное движение — это движение с постоянным касательным ускорением:
Для прямолинейного равнопеременного движения
Полное ускорение равно касательному ускорению. Криволинейное равнопеременное движение (рис. 10.2):
получим значение скорости при равнопеременном движении
После интегрирования будем иметь закон равнопеременного движения в общем виде, представляющий уравнение параболы:
где v0 — начальная скорость движения;
S0 — путь, пройденный до начала отсчета;
a t — постоянное касательное ускорение.
Неравномерное движение
При неравномерном движении численные значения скорости и ускорения меняются.
Уравнение неравномерного движения в общем виде представляет собой уравнение третьей S = f ( t 3 ) и выше степени.
Тема 1.8. Кинематика точки 73
Кинематические графики
Кинематические графики — это графики изменения пути, скорости и ускорений в зависимости от времени.
Равномерное движение (рис. 10.3)
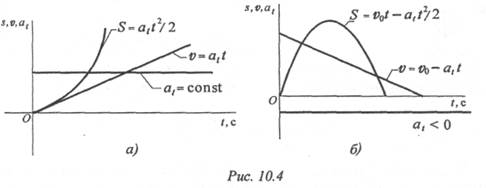
Равнопеременное движение (рис. 10.4)
Примеры решения задач
Пример 1. По заданному закону движения S = 10 + 20t — 5t 2 ([ S ] = м; [ t ] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)
Решение
1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
— начальный путь, пройденный до начала отсчета 10 м;
— начальная скорость 20 м/с;
— постоянное касательное ускорение — = — 5 м/с² ; at =—10 м/с² .
— ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S ´ = 20 — 2 • 5t; v = 20 – 10t; v = 0; t = — = 2 с .
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
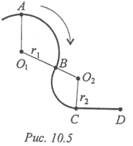
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).
Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (г> = const).
Нормальное ускорение при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Тема 1.8. Кинематика точки 75
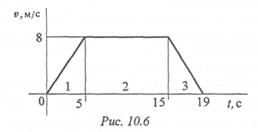
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения.
Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; а2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
Тема 1.8. Кинематика точки 77
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
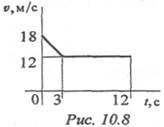
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
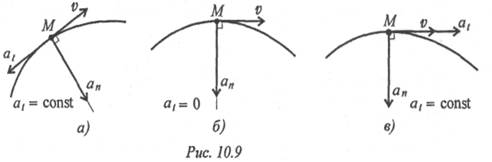
7. Точка движется по дуге. Охарактеризуйте движение точки (рис. 10.9).
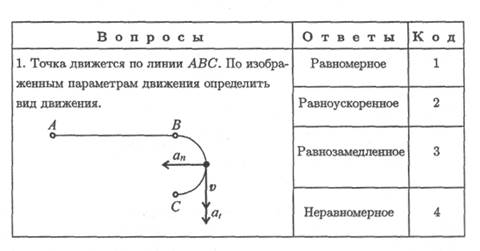
8. Ответьте на вопросы тестового задания.
Темы 1.7, 1.8. Кинематика.
Кинематика точки
Тема 1.9. Простейшие движения твердого тела 79
Тема 1.9. Простейшие движения твердого тела
Иметь представление о поступательном движении, его особенностях и параметрах, о вращательном движении тела и его параметрах.
Знать формулы для определения параметров поступательного и вращательного движений тела.
Уметь определять кинематические параметры тела при поступательном и вращательном движениях, определять параметры любой точки тела.
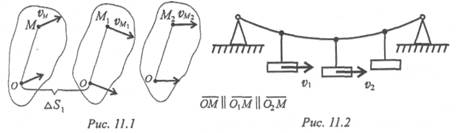
Поступательное движение
Поступательным называют такое движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению (рис. 11.1, 11.2).
При поступательном движении все точки тела движутся одинаково: скорости и ускорения в каждый момент одинаковы. Поэтому для описания движения тела можно рассматривать движение одной его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и криволинейным.
Вращательное движение
При вращательном движении все точки тела описывают окружности вокруг общей неподвижной оси.
Неподвижная ось, вокруг которой вращаются все точки тела, называется осью вращения.
При этом каждая точка движется по окружности, радиус которой равен расстоянию точки до оси вращения. Точки на оси вращения не перемещаются.
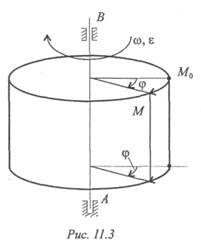
Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры (рис, 11.3):
φ— угол поворота тела, [φ] = рад;
ω — угловая скорость, определяет изменение угла поворота в единицу времени, [ω] = рад/с.
Для определения положения тела в любой момент времени используется уравнение φ = f ( t ).
Следовательно, для определения угловой скорости можно пользоваться
Иногда для оценки быстроты вращения используют угловую частоту вращения п, которая оценивается в оборотах в минуту.
Угловая скорость и частота вращения физически близкие величины ω
Изменение угловой скорости во времени определяется угловым ускорением
Частные случаи вращательного движения
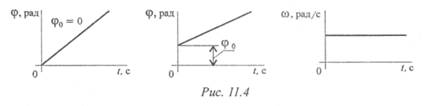
Равномерное вращение (угловая скорость постоянна):
Уравнение (закон) равномерного вращения в данном случае имеет вид:
Тема 1.9. Простейшие движения твердого тела 81
где φ0 — угол поворота до начала отсчета.
Кинематические графики для этого вида движения изображены на рис. 11.4.
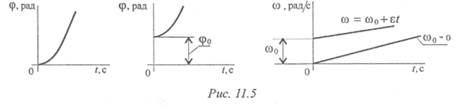
Равнопеременное вращение (угловое ускорение постоянно):
Уравнение (закон) равнопеременного вращения
где ω0 — начальная угловая скорость.
Угловое ускорение при ускоренном движении — величина положительная; угловая скорость будет все время возрастать.
Угловое ускорение при замедленном движении — величина отрицательная; угловая скорость убывает.
Для данного движения кинематические графики представлены, на рис. 11.5.
Скорости и ускорения точек вращающегося тела
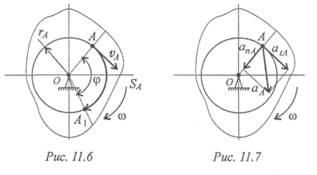
Тело вращается вокруг точки О. Определим параметры движения точки А, расположенной на расстоянии rA от оси вращения (рис. 11.6, 11.7).
Путь точки A : S a = φ r A .
Линейная скорость точки A : v A = ω r A .
Ускорения точки A : at A = ε r A — касательное; ап А = ω 2 r A — нормальное, где r A— радиус окружности, траектории точки А.
Примеры решения задач
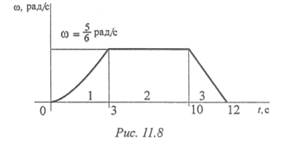
Пример 1. По заданному графику угловой скорости (рис. 11.8) определить вид вращательного движения.
Решение
1. Участок 1 — неравномерное ускоренное движение,ω = φ´; ε = ω‘.
2. Участок 2 — скорость постоянна — движение равномерное, ω = const.
3. Участок 3 — скорость убывает равномерно — равнозамедленное движение, ε = ω‘ 2 r A ; ап A = (12,56) 2 • 0,3 = 47,3м/с 2 .
5. Полное ускорение точек на ободе колеса
Контрольные вопросы и задания
1. Какими кинематическими параметрами характеризуется поступательное движение и почему?
2. Запишите уравнение равномерного поступательного движения твердого тела.
3. Запишите уравнение равнопеременного поступательного движения твердого тела.
4. Запишите уравнения равномерного и равнопеременного вращательного движений твердого тела.
5. Задано уравнение движения тела S = f ( t ). Как определяют скорость и ускорение?
6. Для заданного закона (уравнения) движения φ = 6,28 + 12 t + +3t 2 выберите соответствующий кинематический график движения (рис. 11.11).
7. Для движения, закон которого задан в вопросе б, определите
угловое ускорение в момент t = 5 с.
Тема 1.10. Сложное движение точки.
Сложное движение твердого тела
Иметь представление о системах координат, об абсолютном, относительном и переносном движениях.
Знать разложение сложного движения на относительное и переносное, теорему сложения скоростей.
Знать разложение плоскопараллельного движения на поступательное и вращательное, способы определения мгновенного центра скоростей.
Основные определения
Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениями считают поступательное и вращательное.
Для рассмотрения сложного движения точки выбирают две системы отсчета: подвижную и неподвижную.
Движение точки (тела) относительно неподвижной системы отсчета называют сложным, или абсолютным.
Подвижную систему отсчета обычно связывают с движущимся телом. Движение подвижной системы отсчета относительно неподвижной называют переносным.
Движение материальной точки (тела) по отношению к подвижной системе называют относительным.
Примером может служить движение человека по эскалатору метро. Движение эскалатора — переносное движение, движение человека вниз или вверх по эскалатору — относительное, а движение по отношению к неподвижным стенам станции — сложное (абсолютное) движение.
При решении задач используют теорему о сложении скоростей:
При сложном движении точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной ( ve ) и относительной ( vr ) скоростей:
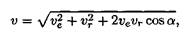
Тема 1.10. Сложное движение точки 87
Плоскопараллельное движение твердого тела
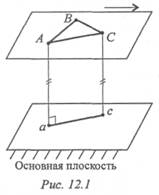
Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются параллельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.
Плоскопараллельное движение можно изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной (рис. 12.1).
Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами: методом разложения сложного движения на поступательное и вращательное и методом мгновенных центров скоростей.
Метод разложения сложного движения на поступательное и вращательное
Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное относительно этого полюса.
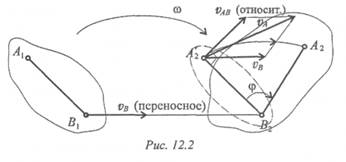
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12.2).
Точка А движется вместе с точкой В , а затем поворачивается
вокруг В с угловой скоростью ш, тогда абсолютная скорость точки А будет равна
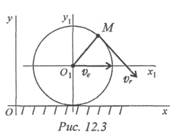
Примером плоскопараллельного движения может быть движение колеса на прямолинейном участке дороги (рис. 12.3).
Скорость точки М v М = v e + v r ,
ve — скорость центра колеса переносная;
vr — скорость вокруг центра относительная.
уОх — неподвижная система координат,
у 1 0 1 Х 1 — подвижная система координат, связанная с осью колеса.
Метод определения мгновенного центра скоростей
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12.4).
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью ω.
Скорость точки А в данный момент равна v a = ω OA ,
т.к. va — линейная скорость точки А, вращающейся вокруг МЦС.
Существуют три способа определения положения мгновенного центра скоростей.
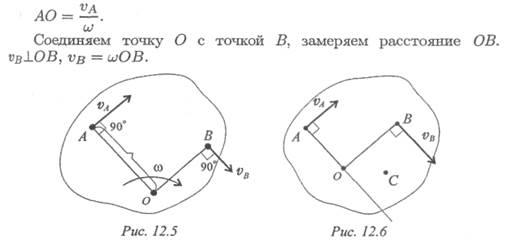
Первый способ. Известна скорость одной точки тела v a и угловая скорость вращения тела ω(рис. 12.5).
Точку О находим на перпендикуляре к вектору скорости v a.
Тема 1.10. Сложное движение точки 89
Второй способ. Известны скорости двух точек тела v a и vB они не параллельны (рис. 12.6).
Проводим из точек А и В два перпендикуляра к известным векторам скоростей.
На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки
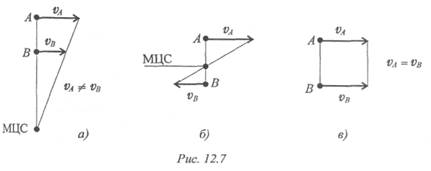
Третий способ. Известны скорости двух точек тела, и они параллельны (v a ║ vB) (рис. 12.7).
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ ( рис. 12.7 ). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.
Примеры решения задач
Пример 1. Рассмотрим механизм, в котором стержень ОА вращается вокруг точки О со скоростью ω. Вдоль стержня перемещается ползун М со скоростью v m (рис. 12.8). Определить абсолютную скорость точки М.
Решение
1. Относительное движение — вдоль стержня; скорость vr = v m .
2. Переносное движение — вращение стержня; скорость ve = ωОМ.
3. Скорость абсолютного движения
Пример 2. Стержень А В соскальзывает вниз, опираясь концами о стену и пол (рис. 12.9). Длина стержня 1,5 м; в момент, изображенный на чертеже, скорость точки В v b = 3 м/с. Найти скорость точки А.
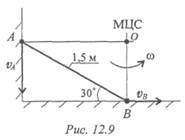
1. Найдем положение МЦС. Скорости точек А и В направлены
вдоль стены и вдоль пола. Восстанавливая перпендикуляры к векторам
скоростей, находим МЦС.
2. По известной скорости v b определяем угловую скорость ω стержня:
Тема 1.10. Сложное движение точки 91
Контрольные вопросы и задания
1. Какое движение называют сложным?
2. Какие движения твердого тела называют простыми?
3. Какие системы координат выбирают при определении скоростей твердых тел при сложном движении?
4. Какое движение считают переносным, а какое — относительным?
5. Сформулируйте теорему сложения скоростей.
6. Какое движение называют плоским?
7. Какие способы применяют для определения скоростей точек тела при плоско-параллельном движении?
8. Что такое мгновенный центр скоростей, как его определяют и для чего используют?
9. Ответьте на вопросы тестового задания.
Темы 1.10, 1.11. Кинематика.
🎥 Видео
Управление скоростью вращения двигателяСкачать

Разновидность неисправности якоря коллекторного мотора. Упали обороты и пошел запах.Скачать

Динамическое торможение. Как мгновенно остановить асинхронный двигатель?Скачать

Регулирование частоты вращения ротора трехфазных асинхронных двигателейСкачать

Принцип работы асинхронного электродвигателяСкачать

Принцип работы синхронного электродвигателяСкачать

Как определить скорость вращения вала электродвигателя и его мощность.Скачать

РОТОР НЕ ВСЕГДА ЯКОРЬ или "маленький ликбез благодаря википедической премудрости"Скачать

Как проверить ротор двигателяСкачать

Как изменить направление вращения трехфазного асинхронного двигателя?Скачать

Как нельзя регулировать скорость вращения электродвигателяСкачать

Модуль №3. Принцип работы асинхронного электродвигателя.Скачать

Мне нужно срочно принять важное решение | недостатки плавного стартаСкачать

ИНДИКАТОР МЕЖВИТКОВЫХ ЗАМЫКАНИЙ 🌟 очень простая СХЕМАСкачать

Проблема с ротором электродвигателя.Скачать

Электродвигатель может разогнать до скорости света? #энерголикбезСкачать

ФЭНШУЙ в СХЕМОТЕХНИКЕ 😁 Простые Схемы решают Сложные ЗадачиСкачать

электро двигатель вращается не в том направлении что делать...Скачать