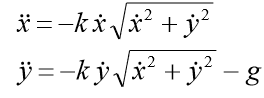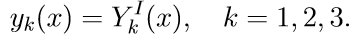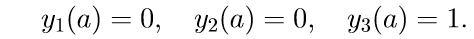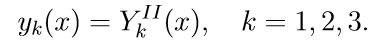ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
научный руководитель канд. физ.-мат. наук, проф.
Лесосибирский педагогический институт – филиал ФГАОУ «Сибирский федеральный университет»
Для изучения объектов или процессов, протекающих в окружающем нас мире, широко используются методы математического моделирования. Математические модели являются мощным средством познания окружающего мира. При этом следует заметить, что построенная математическая модель не может отразить все многообразные и сложные черты изучаемого явления. При моделировании что-то является главным, а что-то – второстепенным, чем можно пренебречь.
Изучение большого круга задач естествознания, техники и механики, биологии, медицины и других отраслей научных знаний показывает, что решение многих из них сводится к математическому моделированию процессов в виде формулы, т. е. в виде функциональной зависимости.
Так, например, некоторые процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью уравнений, в которых кроме независимых переменных и неизвестных функций этих переменных, содержатся производные неизвестных функций (или их дифференциалы). Такие уравнения называются дифференциальными.
Вот почему возможности применения дифференциальных уравнений для решения задач по дисциплинам естественно – научного цикла довольно широки. Обыкновенные дифференциальные уравнения моделируют явления и процессы, которые описываются одной функцией или вектор-функцией одного переменного.
В математическое исследование любой задачи реального мира можно выделить три основных этапа:
1. построение математической модели явления;
2. изучение этой математической модели и получение решения соответствующей математической задачи;
3. приложение полученных результатов к практическому вопросу, из разрешения которого возникла данная математическая модель, и отыскание других вопросов, к которым она применима.
В таблице представлены основные области наук, в которых какое-либо явление или процесс можно записать в виде дифференциального уравнения.
Характеристика составления математической модели
Пример математической модели
1. Установить величины, изменяющиеся в данном явлении, и выявить физические законы, связывающие их.
2. Выбрать независимую переменную и функцию этой искомой переменной.
3. Исходя из условий задачи, определить начальные или краевые условия.
4. Выразить все фигурирующие в условии задачи величины через независимую переменную, искомую функцию и производные этой функции.
5. Исходя из условий задачи и физического закона, которому подчиняется данное явление, составить дифференциальное уравнение.
6. Найти общее решение или общий интеграл дифференциального уравнения.
7. По начальным или краевым условиям найти частное решение.
8. Исследовать полученное решение.
А) Первый закон Ньютона:
Б) Уравнение показательного роста и показательного убывания:
где 
В) Уравнение гармонического колебания:
где 
где 


1. Сделать чертёж и ввести обозначения;
2. Отделить условия. Имеющие место в произвольной точке искомой линии, от условий, выполняющихся лишь в отдельных точках;
3. Выразить все упомянутые в задаче величины через координаты произвольной точки и через значение производной в этой точке, учитывая геометрический смысл производной;
4. По условию задачи составить дифференциальное уравнение;
5. Найти общее решение этого уравнения и получить из него с помощью начальных условий уравнение искомой линии.
Формула зеркала, собирающего все параллельные лучи в одну точку:
При создании математической модели используют физические закономерности, выявленные при экспериментальном изучении объекта моделирования. Так, например, математическая модель кровообращения основано на законах гидродинамики.
Модель хищник – жертва:
где 


Сущность химических реакций сводится к разрыву связей в исходных веществах и возникновению новых связей в продуктах реакции. При этом общее число атомов каждого элемента до и после реакции остаётся постоянным.
Закон действующих масс:
где 

Базовая математическая модель в области финансов формулируется в терминах стохастических процессов, приводящих, таким образом, к стохастическим дифференциальным уравнениям. Время и недостоверность являются главными элементами моделирования финансового поведения экономических агентов.
Модель фондового (биржевого) ценообразования:
где 

Компартментальное моделирование распространено в медицине и биологии. Согласно определению американского фармаколога и биохимика Шеппарда компартмент — это некоторое количество вещества, выделяемое в биологической системе и обладающее свойством единства, поэтому в процессах транспорта и химических преобразований его можно рассматривать как целое. Например, в качестве особых компартментов рассматривают весь кислород в легких, всю углекислоту в венозной крови, количество введенного препарата в межклеточной жидкости, запас гликогена в печени и т. п. Модели, в которых исследуемая система представляется в виде совокупности компартментов, потоков вещества между ними, а также источников и стоков всех веществ, называются компартментальными.
Модель роста опухоли:
где 

В заключение отметим, что математическая модель является основой математически оформленной теории того или иного явления, а аппарат дифференциальных уравнений нашел большое применение в математическом моделировании.
Результативность математического моделирования подтверждена всей человеческой практикой, это сильное средство научного исследования, которое используют в каждой конкретной области науки.
- Численное решение математических моделей объектов заданных системами дифференциальных уравнений
- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- ДИПЛОМНАЯ РАБОТА Использование дифференциальных уравнений в частных производных для моделирования реальных процессов.
- Глава 2. Уравнения параболического типа.
- Глава 1. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- Так как иначе мы имели бы
- найти те значения параметра , при которых существуют нетривиальные решения задачи:
- Глава 2. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.
- Рис. 3.1. Сферическая система координат для изучения
- В случае электрических колебаний из уравнения (6) получим
- В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.
- 🌟 Видео
Видео:Дифференциальные уравнения. 11 класс.Скачать

Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
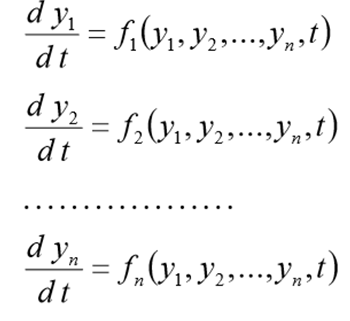
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
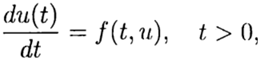

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 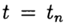

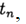


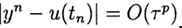

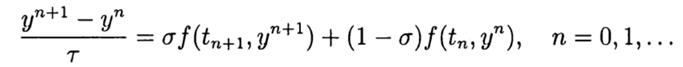
При 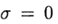
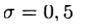
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
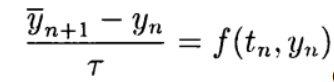
а на этапе корректора (уточнения) — схема
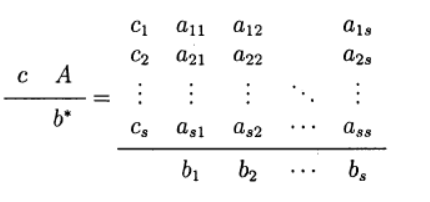
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
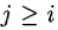

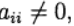

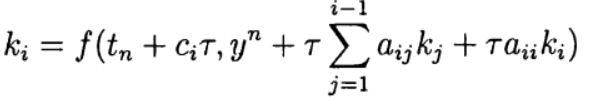
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
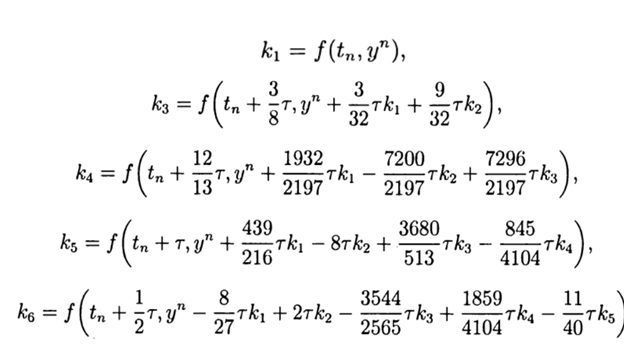
С учётом(9) общее решение имеет вид:
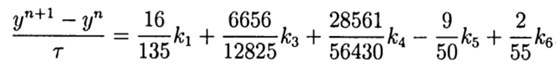
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
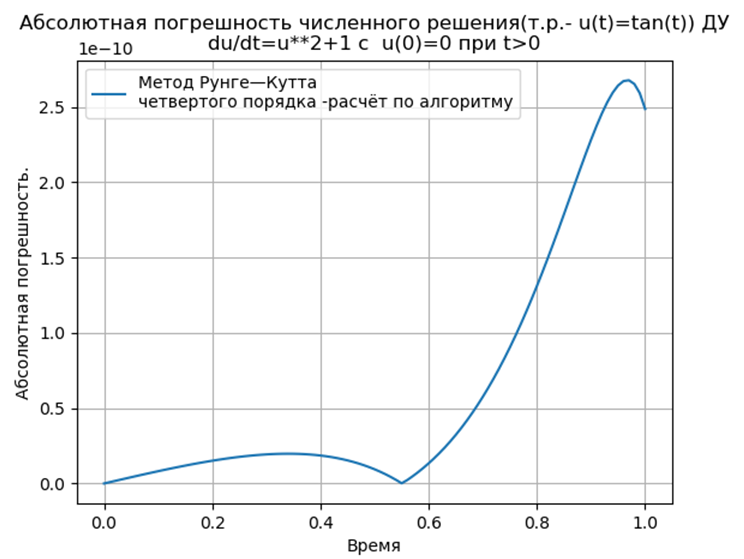
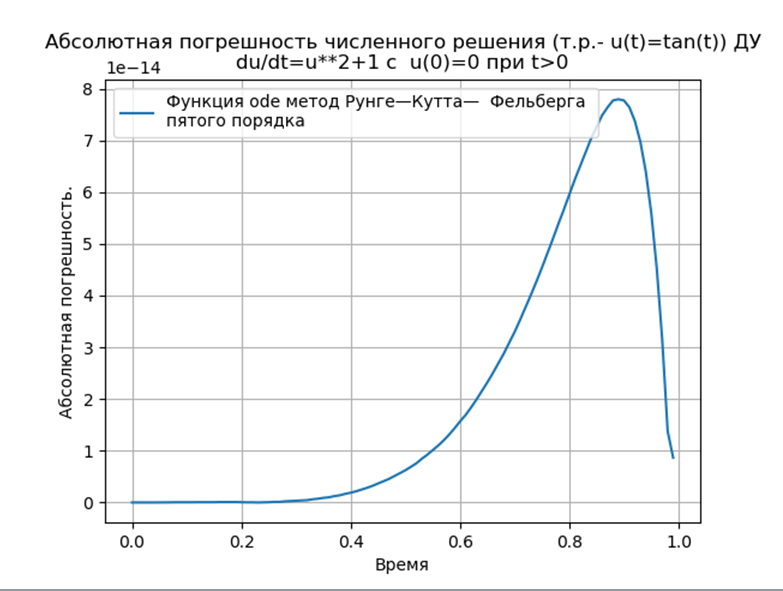
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
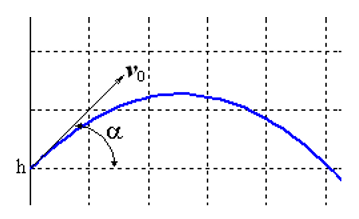
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 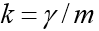
К системе следует добавить начальные условия: 

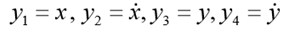
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
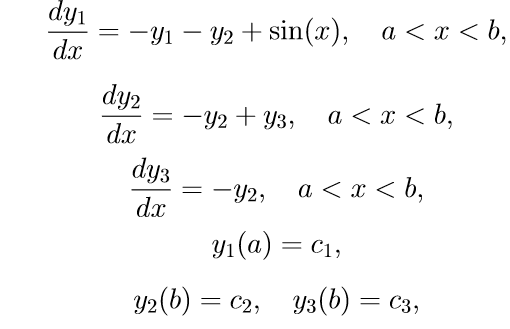
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 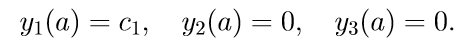
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 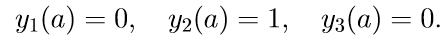
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 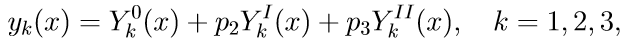
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

ДИПЛОМНАЯ РАБОТА Использование дифференциальных уравнений в частных производных для моделирования реальных процессов.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Использование дифференциальных уравнений в частных производных для моделирования реальных процессов.
Глава 1. Уравнения гиперболического типа.
§1.1. Задачи, приводящие к уравнениям гиперболического типа..………………5
1.1.2. Уравнение электрических колебаний в проводах…….………………8
§1.2. Метод разделения переменных ……………………………………………..10
1.2.1. Уравнение свободных колебаний струны….………………………… 10
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Глава 2. Уравнения параболического типа.
§2.1. Задачи, приводящие к уравнениям параболического типа………………..17
2.1.1. Уравнение распространения тепла в стержне.………………………. 17
2.1.2. Распространение тепла в пространстве.……………………………… 19
Глава 3. Моделирование с помощью дифференциальных уравнений в частных производных.
§3.1. Дифракция излучения на сферической частице…………………………… 29
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.
Классические уравнения математической физики являются линейными. Особенность линейных уравнений состоит в том, что если U и V – два решения, то функция U + V при любых постоянных и снова является решением. Это обстоятельство позволяет построить общее решение линейного дифференциального уравнения из фиксированного набора его элементарных решений и упрощает теорию этих уравнений.
Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.
Круг вопросов математической физики тесно связан с изучением различных физических процессов. Сюда относятся явления, изучаемые в гидродинамике, теории упругости, электродинамике и т.д. Возникающие при этом математические задачи содержат много общих элементов и составляют предмет математической физики.
Постановка задач математической физики, будучи тесно связанной с изучением физических проблем, имеет свои специфические черты. Так, например, начальная и конечная стадии процесса носят качественно различный характер и требуют применения различных математических методов.
Круг вопросов, относящихся к математической физике, чрезвычайно широк. В данной работе рассматриваются задачи математической физики, приводящие к уравнениям с частными производными.
Расположение материала соответствует основным типам уравнений. Изучение каждого типа уравнений начинается с простейших физических задач, приводящих к уравнениям рассматриваемого типа.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Глава 1. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
§1.1. Задачи, приводящие к уравнениям гиперболического типа.
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа
называется волновым уравнением. К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д.
1.1.1. Уравнение колебаний струны.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины 


Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией 
Так как мы рассматриваем малые отклонения струны в плоскости 


Рассмотрим элемент струны 

На концах этого элемента, по касательным к струне, действуют силы Т. Пусть касательные образуют с осью Ox углы 




(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть 



Сокращая на 


Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция 

Пусть, например, как мы предполагали, концы струны при 


Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f ( x ). Таким образом, должно быть

Далее, в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией 

Условия (3’) и (3’’) являются начальными условиями.
Замечание. В частности, может быть 




1.1.2. Уравнение электрических колебаний в проводах.
Как указывалось выше, к уравнению (1) приводит и задача об электрических колебаниях в проводах. Электрический ток в проводе характеризуется величиной i ( x , t ) и напряжением v ( x , t ), которые зависят от координаты x точки провода и от времени t . Рассматривая элемент провода 





где R и L – сопротивление и коэффициент индуктивности, рассчитанные на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию v . Сокращая на 

Далее, разность токов, выходящего из элемента 

Она расходуется на зарядку элемента, равную 



Уравнения (5) и (6)принято называть телеграфными уравнениями.
Из системы уравнений (5) и (6) можно получить уравнение, содержащее только искомую функцию i ( x , t ), и уравнение, содержащее только искомую функцию v ( x , t ). Продифференцируем члены уравнения (6) по x ; члены уравнения (5) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
Подставляя в последнее уравнение выражение 

Аналогичным образом получается уравнение для определения v ( x , t ):

Если пренебречь утечкой через изоляцию 

где обозначено: 
§1.2. Метод разделения переменных.
1.2.1. Уравнение свободных колебаний струны.
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения
Видео:Моделирование на основе дифференциальных уравненийСкачать

удовлетворяющее однородным граничным условиям

и начальным условиям

Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.
Поставим основную вспомогательную задачу: найти решение уравнения
Видео:Teaching towards a modelling perspective // Моделирование систем дифференциальных уравненийСкачать

не равное тождественно нулю, удовлетворяющее однородным граничным условиям

и представимое в виде произведения

Подставляя предполагаемую форму решения (12) в уравнение (1), получим:
или, после деления на XT ,

Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹ 

где 
Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X ( x ) и T ( t )


Граничные условия (11) дают:
Отсюда следует, что функция X ( x ) должна удовлетворять дополнительным условиям:
X (0) = X ( 
Видео:"Мы зажигаем свои звёзды" О роли нелинейных дифференциальных уравненийСкачать

Так как иначе мы имели бы
в то время как задача состоит в нахождении нетривиального решения. Для функции T ( t ) в основной вспомогательной задаче никаких дополнительных условий нет.
Таким образом, в связи с нахождением функции X ( x ) мы приходим к простейшей задаче о собственных значениях:
найти те значения параметра  , при которых существуют нетривиальные решения задачи:
, при которых существуют нетривиальные решения задачи:

а также найти эти решения. Такие значения параметра 
Рассмотрим отдельно случаи, когда параметр 
При 
Граничные условия дают:
Но в рассматриваемом случае 

Х (х)
При 
Граничные условия дают:
т. е. С 1 = 0 и С 2 = 0 и, следовательно,
Х (х)
При 
Граничные условия дают:
Если Х(х) не равно тождественно нулю, то D 2 

где n — любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях
Этим собственным значениям соответствуют собственные функции
где D n – произвольная постоянная.
Итак, только при значениях 

существуют нетривиальные решения задачи (11)

определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям 

где A n и B n – произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции

являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t . Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций (x) и (x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений

также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить A n и B n . Потребуем, чтобы функция (24) удовлетворяла условиям (10)

Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f ( x ), заданная в промежутке 


Если функции (x) и (x) удовлетворяют условиям разложения в ряд Фурье, то


Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить

чем полностью определяется функция (24), дающая решение исследуемой задачи.
Итак, мы доказали, что ряд (24), где коэффициенты A n и B n определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u ( x , t ), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция 

Видео:Математика это не ИсламСкачать

Глава 2. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
§2.1. Задачи, приводящие к уравнениям гиперболического типа.
Уравнение распространения тепла в стержне.
Рассмотрим однородный стержень длины 
Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = 
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х 1 и х 2 (х 2 – х 1 = 


то же самое с абсциссой х 2 :

Приток 



Этот приток тепла за время 


где с – теплоемкость вещества стержня, 

Приравнивая выражения (4) и (5) одного и того же количества тепла 
Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.
Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 
u ( 
Физическое условие (7) (начальное условие) соответствует тому, что при 

Доказывается, что уравнение (6) имеет единственное решение в области 
2.1.2. Распространение тепла в пространстве.
Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку 

где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке 
где 
Подставляя выражение 


Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:




Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:

где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (11) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время 
Рассмотрим элементарный объем 



где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время 
Но это есть тепло, поступающее в объем V за время 
Сокращая на 

Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, 
полагая F = k grad u:
Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:
Применив теорему о среднем к тройному интегралу, стоящего слева, получим :

где P (x, y, z) – некоторая точка объема V.
Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,

Подставляя в уравнение (15), получаем:

Если k – постоянное, то
и уравнение (15) в этом случае дает:
или, положив

Коротко уравнение (17) записывается так:
где 
Пусть имеем тело 

u (x, y, z, 0) = φ (x, y, z). (18)
Кроме того, должна быть известна температура в любой точке М поверхности 
u ( М , t) = ψ ( М , t). (19)
(Возможны и другие граничные условия.)
Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:

уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:
u ( М , t) = ψ ( М , t),
где φ и ψ – заданные функции, М – точка границы С.
Если же функция u не зависит ни от z, ни от y, то получаем уравнение
— уравнение распространения тепла в стержне.
§2.2. Температурные волны.
Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.
Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 
найти ограниченное решение уравнения теплопроводности

u (0, t) = A cos 
Предполагается, что функции u ( x , t ) и ( t ) ограничены всюду, т.е.
Запишем граничное условие в виде

Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.
Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию
Итак, рассмотрим задачу:

Ее решение будем искать в виде

где 

Подставляя выражение (4) в уравнение (3) и граничное условие, находим:

Для u ( x , t ) имеем:

Действительная часть этого решения

удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде

На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:
1.Амплитуда колебаний экспоненционально убывает с глубиной

т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).
2. Температурные колебания в почве происходят со сдвигом фазы. Время 
(второй закон Фурье).
3. Глубина проникновения тепла в почву зависит от периода колебаний температуры на поверхности. Относительное изменение температурной амплитуды равно
Эта формула показывает, что чем меньше период, тем меньше глубина проникновения температуры. Для температурных колебаний с периодами Т1 и Т2 глубины x 1 и x 2, на которых происходит одинаковое относительное изменение температуры, связаны соотношением
(третий закон Фурье). Так, например, сравнение суточных и годовых колебаний, для которых Т2 = 365 Т1, показывает, что
т.е. что глубина проникновения годовых колебаний при одинаковой амплитуде на поверхности была бы в 19,1 раза больше глубины проникновения суточных колебаний.
Следует, однако, иметь в виду, что изложенная здесь теория относится к распространению тепла в сухой почве или горных породах. Наличие влаги усложняет температурные явления в почве, при замерзании происходит выделение скрытой теплоты, не учитываемое этой теорией.
Температуропроводность является одной из характеристик тела, важных для изучения его физических свойств, а также для различных технических расчетов. На изучении распространения температурных волн в стержнях основан один из лабораторных методов определения температуропроводности.
Пусть на конце достаточно длинного стержня поддерживается периодическая температура 
где Т – период, и взяв температурные волны, соответствующие каждому слагаемому, получим, что температура u ( x , t ) для любого x будет периодической функцией времени и ее n -я гармоника равна
Эта формула показывает, что если произвести измерение температуры в каких-нибудь двух точках, x 1 и x 2, за полный период, то, находя коэффициенты a n ( x 1), b n ( x 1), a n ( x 2), b n ( x 2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а 2 .
Видео:1. Что такое дифференциальное уравнение?Скачать

Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.
§3.1. Дифракция излучения на сферической частице.
Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в случае монохроматического излучения частоты 



где 
Задача о разыскании шести неизвестных функций (
Пусть на сферическую частицу радиуса а, центр которой совмещен с началом координат, в отрицательном напрвлении оси Oz падает линейно поляризованная плоская волна (рис 4.). Ось Ox является направлением электрических колебаний, а ось Oy – магнитных. Электрическое и магнитное поля в падающей волне описываются формулами:

г


Рис. 3.1. Сферическая система координат для изучения
дифракции света на шаре.
В дальнейшем в промежуточных формулах всюду будет опущен множитель Е 0 , который будет внесен в окончательные выражения для полей.
В сферической системе координат, в которой естественно решать данную задачу, уравнения Максвелла (1) имеют вид:




Падающее поле возбуждает в шаре внутреннее поле, а во внешнем пространстве – дифрагированное поле, причем все эти поля должны иметь оду и ту же временную зависимость, т.е. частоту. Произвольное электромагнитное поле будем представлять как суперпозицию двух типов колебаний. Первый тип назовем электрическими колебаниями и будем считать, что у этих колебаний радиальная составляющая магнитного поля во всех точках равна нулю:

Второй тип – магнитные колебания:

Видео:Модели на основе дифференциальных уравнений с запаздыванием.Скачать

В случае электрических колебаний из уравнения (6) получим
Это соотношение, очевидно, будет удовлетворено, если предположим, что 



Подставляя эти соотношения в формулы (4) и (5) получим
Этим соотношениям можно удовлетворить, если положить 





тогда как (7) и (8) приводятся к одному и тому же волновому уравнению для функции
Используя указанные выше соотношения и заменяя в выражении для 


которые выражают все составляющие полей для случая 


В общем случае в поле присутствуют колебания обоих типов. Для составляющих полей получим при этом следующие выражения:

Функции U 1 и U 2 являются решением волнового уравнения.

которое будем решать по методу Фурье (значок у U временно опущен, он появится при рассмотрении граничных условий, которые для U 1 и U 2 различны). В качестве частного решения положим

Подставляя (16) в (13) и разделяя переменные, получим для f и Y следующие уравнения:


Уравнение для Y имеет однозначное и непрерывное решение на всей сфере только для 

где 



Это уравнение Бесселя и его решением являются цилиндрические функции с полуцелым индексом 

Из всех цилиндрических функций только бесселевы функции первого рода 




тогда частное решение, очевидно, следует представить в виде суперпозиции частных решений с неопределенными коэффициентами, которые вычисляются из граничных условий. Граничные условия для потенциалов U 1 и U 2 на шаре получаются из требования непрерывности тангенциальных (



где U a – потенциал дифрагированного поля, а U i – внутреннего.
Представим теперь электрический и магнитный потенциалы падающей волны также в виде рядов по 

Тогда после преобразований получим:

Потенциалы 



Коэффициенты 









Аналогичная система получается для 


Решая эти системы относительно 


Аналогичные выражения получаются и для 


Штрихи всюду означают производные по аргументу, указанному под знаком функции ( 





и применяя асимптоматические выражения для функций 


Согласно этим формулам, дифрагированное поле представляется в виде сумм отдельных парциальных волн. Интенсивность возбуждения 


Поле вне частицы 



Средняя по времени величина вектора потока энергии определяется

где 






где J 0 – интенсивность падающего излучения, 





Рассмотрим интеграл в (39). Имеем 

Сумма будет иметь общий множитель 



Заключение
В дипломной работе приведены некоторые примеры применения дифференциальных уравнений для моделирования таких реальных процессов, как колебания струны, электрические колебания в проводах, распространение тепла в стержне и пространстве, распространение температурных волн в почве, дифракция излучения на сферической частице.
Работа начинается с рассмотрения простейших задач, приводящих к дифференциальным уравнениям гиперболического типа (колебания струны, электрические колебания в проводах). Затем рассматривается один из методов решения уравнений данного типа. Во второй главе рассматриваются дифференциальные уравнения параболического типа (распространение тепловых волн) и одно из приложений к данной сфере – температурные волны. В третьей главе рассматривается вывод уравнения дифракции излучения на сферической частице.
Вследствие большого объема теории по применению дифференциальных уравнений для моделирования реальных процессов в данной дипломной работе не мог быть рассмотрен весь материал.
Видео:Моделируем курс биткойна (дифференциальные уравнения)Скачать

В заключение хотелось бы отметить особую роль дифференциальных уравнений при решении многих задач математики, физики и техники, так как часто не всегда удается установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается вывести дифференциальное уравнение, позволяющее точно предсказать протекание определенного процесса при определенных условиях.
Н. С. Пискунов «Дифференциальное и интегральное исчисления», М., «Наука», 1972, том. 2.
И. М. Уваренков, М. З. Маллер «Курс математического анализа», М., «Просвещение», 1976.
А. Н. Тихонов, А. А. Самарский «Уравнения математической физики», М., «Наука», 1972.
Владимиров В. С. «Уравнения математической физики», М., «Наука», 1988.
1 Это предположение эквивалентно тому, что мы пренебрегаем величиной 

🌟 Видео
Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Разностные уравнения | Решение задачСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Математическое моделирование - Лекция 1 (09.02.07)Скачать













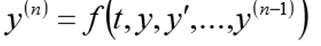
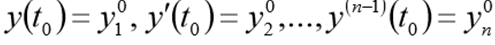


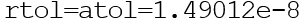
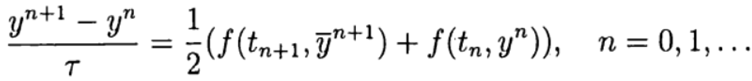
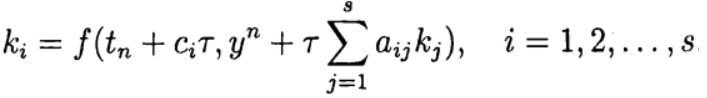
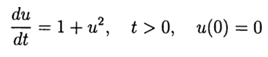 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга