Рисунки с помощью графиков уравнений (8 видео)

Интегрированный урок (алгебра + информатика) по теме «Рисуем графиками функций». 8-й класс

Класс: 8

Тема (математика): Преобразования графиков функций.

Тема (информатика): Построение графиков в MS Excel.

Цели урока:

Образовательные:
- повторение знаний по преобразованию графиков функций,
- применение приобретенных умений и навыков графического изображения в процессе решения задач по математике и информатике;
- формирование практических навыков построения графиков в программе Excel.
Развивающие:
- развитие умений выделять главное,
- развитие речи, эмоций, логического мышления учащихся,
- активизация познавательной и творческой активности учащихся.
Воспитательные:
- формирование интереса к предмету, навыков контроля и самоконтроля, чувства ответственности, самостоятельности, деловых и коммуникативных качеств учащихся.

Задачи урока:

Повторить виды преобразований графика функции y = f(x):
- y = – f(x) ;
- y = kf(x);
- y = f(x) + а;
- y = f(x – b);
- y = f(x – b) + а.
Использовать изученные виды преобразований для построения рисунка с помощью графиков.
Использовать умения построения графиков в одной системе координат с помощью программы Excel для получения некоторого изображения.
Продолжить формирование у учащихся потребности использования информационных технологий в решении графических заданий по математике.
Продемонстрировать применение полученных знаний на практике и для решения задач из смежных дисциплин.

Структура урока:

Организационный момент (объявление темы, цели и задач урока).
Актуализация знаний (повторение видов преобразований графиков функций)
Повторение темы «Преобразования графиков функций»:
- выполнение задания на построение графиков функций с помощью различных видов преобразований;
- построение рисунка в тетради с помощью графиков функций на заданной области определения.
Повторение темы «Построение графиков функций с помощью программы Excel:
- повторение особенностей ввода формул и построения графиков в программе Excel.
- практическая работа «Рисуем графиками функций в программе Excel».
- проверка практической работы, анализ ошибок и выставление оценок.
Постановка домашнего задания.
Подведение итогов урока, рефлексия.

1. Организационный момент

Сегодня мы проводим интегрированный урок, в ходе которого попробуем совместить два предмета: математику и информатику. Нам предстоит повторить преобразования графиков функций и использовать эти знания для выполнения заданий по математике и информатике на построение различных изображений.

2. Актуализация знаний

Для повторения изученных видов преобразований графиков необходимо выполнить предложенное задание.

Задание для фронтальной работы: установите соответствие между предложенными графиками и формулами функций, дайте характеристику данному виду преобразований (рис.1, 2).

3. Повторение темы «Преобразования графиков функций»

Применение рассмотренных видов преобразований осуществляется при выполнении двух следующих заданий, которые учащиеся выполняют в тетрадях. Один ученик выполняет задание на интерактивной (либо обычной) доске. Графики обозначаются разными цветами.

Задание 1: постройте графики функций с помощью изученных видов преобразований

Первый график должен быть построен обязательно на доске, второй рассчитан на учеников, быстро выполнивших задание, либо может быть использован как резервный в конце урока для самостоятельной работы учащихся, быстро справившихся с практической работой.

Задание 2: Постройте рисунок с помощью графиков функций (рис.3):

Графики 4),5),6),7) до пересечения с графиком
А теперь попробуем получить рисунки в программе Excel.

4. Повторение темы «Построение графиков функций с помощью программы Excel:

Для повторения темы на данном этапе урока необходимо провести фронтальный опрос учащихся с целью актуализации знаний по информатике, необходимых для выполнения практической работы.

Вопросы для устной фронтальной работы:

Как задать диапазон значений для переменной Х?
Как задать диапазон значений для переменной У?
Как показать, что в ячейку будет введена формула?
Какие правила ввода формул вы знаете?
Какими символами обозначаются действия умножения, деления, возведения в степень?
Может ли формула в программе Excel содержать переменную Х? А что вместо Х она должна содержать?
Как построить несколько графиков в одной системе координат?
Какой тип диаграмм надо выбрать для построения графика функции?
Как изменить цвет графика?

Практическая работа «Рисуем графиками функций в программе Excel».

Все ученики получают карточки с заданиями. Задания (зонтик, очки, кит) берутся из источника [6]. В одной системе координат необходимо построить графики всех функций на указанных промежутках. Если все будет выполнено верно, то получится картинка. За работу каждому будет выставлена отметка с учетом объема выполненной работы и допущенных ошибок. Работу сохранить на Рабочий стол и не закрывать.

На данном этапе учащиеся осуществляют самоконтроль:

определяют, какие элементы рисунка «не вписываются» в общую картину,
чем это было вызвано (ошибки при вводе формулы, при задании диапазона значений и т.п.), опираясь на полученные на уроках математики знания о различных видах преобразований, вносят изменения и оценивают, как они повлияют на вид рисунка. Во время работы учитель проходит по классу и оценивает работу учащихся.

На следующем этапе учитель показывает с помощью проектора, какие рисунки должны получиться у учащихся, объявляет оценки за выполненную работу, проводит с помощью учеников анализ типичных неточностей и ошибок.

5 . Постановка домашнего задания

По алгебре (творческое задание): придумать рисунок с помощью графиков 7-8 функций. Изобразить его в координатной плоскости, записать используемые функции на заданной области определения.
По информатике: построить с помощью программы Excel рисунок по заданным формулам функций из того же источника [6] (бабочка и лягушка).

6. Подведение итогов урока, рефлексия

Подведение итогов урока осуществляется в форме беседы, в ходе которой обсуждается вопрос: в каких сферах человеческой деятельности могут применяться графики функций.
На этапе рефлексии ученикам предоставляется возможность оценить свою работу, а также ответить на вопросы: получилось ли достигнуть цели урока, достаточно ли было знаний для выполнения предложенных заданий, какие задания требуют дополнительного внимания.

Список использованной литературы

Алгебра,8 класс: учеб. для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е.Феоктистов.–10-е изд., испр. – М.: Мнемозина, 2010.–384с.
Босова Л.Л. Информатика и ИКТ: учебник для 7 класса / Л.Л. Босова. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2010. – 229 с.
Цукарь А.Я. Рисуем графиками функций // Математика в школе. – 1999. – №4. – с. 80-81

Содержание

Научно — практическая работа» Первые шаги в науку»: «Рисуем графиками линейных функций»
Скачать:
Предварительный просмотр:
Проектная работа по теме «Построение рисунков с помощью графиков функций» (9 класс)
Выберите документ из архива для просмотра:
Описание презентации по отдельным слайдам:
🌟 Видео

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Научно — практическая работа» Первые шаги в науку»: «Рисуем графиками линейных функций»

Цель работы: научиться создавать простые рисунки и сюжеты с помощью графиков линейных функций с заданными ограничениями в сервисе DESMOS-графический калькулятор.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Скачать:

Вложение	Размер
67_nesmina_a.l_matematika.docx	111.27 КБ

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Предварительный просмотр:

ХIV городская научно-практическая конференция школьников «Первые шаги в науку»

Возрастная категория: «Юниор»

«Рисуем графиками линейных функций»

Несмина Анастасия Леонидовна

г.о. Тольятти, МБУ «Лицей № 67», 7 класс

Столярчук Лилия Геннадьевна,

учитель математики первой категории, МБУ «Лицей № 67»

2.1. Элементарные функции и их графики………………5

2.2. Линейная функция и ее график………………………6

2.3. Рисование графиками линейных функций………….7

Каждый год счастливые родители ведут своих детей в школу. И далее дорога для большего числа учащихся составляет 11 лет упорного труда в получении знаний. Математика сопровождает нас на всем пути, но, к сожалению, не у всех ребят есть прирожденная склонность к ней. Возникает необходимость для поиска методов воздействия на учащихся, которые могли бы повысить стимул приобретения и расширения знаний. Как заставить ученика работать с удовольствием, а не из-под палки? Как сделать так, чтобы он захотел чему то научиться? Математика – одна из важнейших наук на земле и именно поэтому есть необходимость развивать у детей интерес к этой науке. А это означает, что задания в математике должны быть такими, чтобы постоянно была пища для размышлений и, даже, для творческого полета.

Тема исследовательской работы : « Рисуем графиками линейных функций ».

Гипотеза : « графиками линейных функций можно рисовать отдельные объекты и даже целые сюжеты».

Цель : научиться создавать простые рисунки и сюжеты с помощью графиков линейных функций с заданными ограничениями в сервисе DESMOS-графический калькулятор.

Объект исследования : линейная функция и ее график.

Предмет исследования : рисование графиками линейной функции.

1. Изучить разнообразную литературу по теме: «Линейная функция и ее график»

2. Создать авторские рисунки графиками линейных функций в сервисе DESMOS-графический калькулятор;

3. Предложить одноклассникам построить рисунки по заданным функциям с ограничениями;

4. Предложить одноклассникам создать авторские рисунки графиками линейных функций в сервисе DESMOS-графический калькулятор;

6. Выполнить оценку результатов своей работы и сделать выводы.

поиск, анализ и синтез литературы и программного обеспечения;
практическое применение знаний, умений и навыков;
обобщение;

Понятие «функция» одно из важнейших в математике. С помощью функции описываются различные процессы и явления: химические, статистические, физические, природные и т.д.

Актуальность работы заключается в том, что при выполнении творческих заданий на создание изображений графиками линейных функций, развиваются художественные способности учащихся, которые лежат в основе различных профессий: дизайнер, архитектор, скульптор и т.д., кроме того, повышается интерес к изучению темы: «Линейная функция и ее график». Красота и эстетика математики в школе в особой мере проявляется именно в «красивых» и творческих заданиях.

Рисование графиками линейных функций заставляет воочию увидеть неразрывную связь красоты и математики, непосредственно соприкоснуться с миром прекрасного. Вместо однообразных упражнений по изучаемой теме можно предложить ребятам творческий подход и тогда математика становится интересной, удивительной и красивой.

Относительная «новизна» заданий, неожиданная фабула интригует, а положительные эмоции включают второе дыхание в получении знаний. Такие нестандартные упражнения послужат достаточно хорошей школой для приобретения необходимых основ мышления, владея которыми можно решать любые задачи. Кроме того, чтобы облегчить дальнейшее изучение специальных функций в школе, нужно научиться свободно оперировать графиками элементарных функций.

2. Основное содержание.

2.1 Элементарные функции и их графики

Знакомство и изучение свойств различных функций и их графиков занимает важное место и в школьной математике, и в следующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве предметов узкого профиля. Например в экономике – это функции издержек, полезности, функции спроса, предложения и потребления, в радиотехнике – функции управления и функции отклика, в статистике – функции распределения и т.д.

Определение: зависимость переменной у от переменной х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией. у = f(х), где х – независимая переменная (аргумент), у – зависимая переменная (функция).

Область определения функции D(f)- множество, на котором задаётся функция. Иначе: множество значений, которые может принимать аргумент.

Область значений функции E(f)- множество, состоящее из всех значений, которые принимает функция.

График функции – множество точек на координатной плоскости, координатами которых являются пары чисел (х; у), где х – значение аргумента, у – соответствующее ему значение функции.

1. Линейная функция y = kx + m

График функции – прямая.

2. Функция y = kx² (k ≠ 0)

График функции – парабола.

3. Квадратичная функция y = ax² + bx + c

График функции – парабола

4. Функция обратной пропорциональности y =

График функции – гипербола.

График функции – ветвь параболы, перевернутая «набок».

График функции – объединение двух лучей

3. y = xⁿ (n = 3, 5, 7, 9…)

График функции – кубическая парабола (при n=3)

2.2. Линейная функция и ее график.

Линейная функция y = kx + m, график функции – прямая.

Коэффициент k отвечает за угол наклона (k>0 – угол острый, k 0 – вверх, m

у = kx – частный случай линейной функции при m=0 (прямая пропорциональность)

В этом случае график функции обязательно проходит через начало координат.

Свойства линейной функции y = kx + m

2) Возрастает, если k > 0; убывает, если k

3) Не ограничена ни снизу, ни сверху

4) Нет ни наибольшего, ни наименьшего значений

Чтобы составить уравнение линейной функции надо:

взять координаты двух точек, через которые проходит прямая ( x 1 ,y 1 ) ( x 2 ,y 2 );
подставить эти координаты в уравнение линейной функции и получить систему двух уравнений:
выразить из первого уравнения m = у 1 — k х 1 ;
подставить во второе у 2 = k х 2 + у 1 — k х 1 ;
найти значение k = ;
подставить значение k в формулу m = у 1 — k х 1 .

Например, мы выяснили, что график линейной функции (прямая) проходит через точки с координатами (5;2) и (4:1). Действуем по плану: составим систему уравнений

Из первого уравнения выразим m : m=2-5k, подставим значение m во второе уравнение и найдем k : 1=4k+2-5k, k =1. Далее в уравнение линейной функции подставляем значения коэффициентов k и m и получаем искомое уравнение прямой: у=х-3 .

2.3. Рисование графиками линейных функций на уроке математики

Видео:Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Проектная работа по теме «Построение рисунков с помощью графиков функций» (9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Задания группам.docx

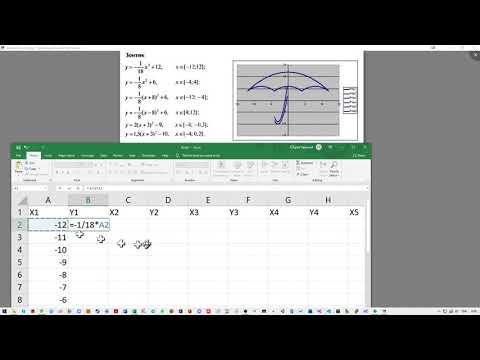
Построить рисунок «Зонтик» [5] по заданным уравнениям графиков функций:

у = (-1/18) х 2 +12, xϵ[ -12;12 ] ;

у = (-1/8) х 2 +6, xϵ[ -4;4 ] ;

у = (-1/8) (х+8) 2 , xϵ 12; -4 ] ;

у = (-1/8) (х-8) 2 , xϵ[ 4;12 ] ;

у = 2(х+3) 2 -9, xϵ [ -4; -0,3 ] ;

у = 1,5(х+3) 2 -10, xϵ [ -4; -0,2 ] .

Построить рисунок «Очки» [5] по заданным уравнениям графиков функций:

у = (-1/16) (х+5) 2 +2, xϵ [ -9; -1 ] ;

у = (-1/16) (х-5) 2 +2, xϵ[ 1;9 ] ;

у = (1/4) (х+5) 2 -3, xϵ [ -9; -1 ] ;

у = (1/4) (х-5) 2 -3, xϵ[ 1;9 ] ;

у = -(х+7) 2 +5, xϵ [ -9; -6 ] ;

у = — (х-7) 2 +5, xϵ [ 6; 9 ] ;

у = 0,5х 2 +1,5, xϵ [ -1; 1 ] .

Построить рисунок «Лягушка» [5] по заданным уравнениям графиков функций:

у = (-3/49) х 2 +8, xϵ[ -7;7 ] ;

у = (4/49) х 2 +1, xϵ[ -7;7 ] ;

у = -0,75 (х+4) 2 +11, xϵ [-6,8; -2];

у = -0,75 (х-4) 2 +11, xϵ [2;6,8];

у = -(х+4) 2 +9, xϵ [-5,8; -2,8];

у = — (х-4) 2 +9, xϵ [2,8;5,8];

у = (4/9) х 2 -5, xϵ [-4;4].

у = (4/9) х 2 -9, xϵ [-5,2;5,2];

у = (-1/16) (х+3) 2 -6, xϵ [-7; -2,8];

у = (-1/16) (х-3) 2 -6, xϵ [2,8;7];

у = (1/9) (х+4) 2 -11, xϵ [-7;0];

у = -(1/9) (х-4) 2 -11, xϵ [0;7];

у = -(х+5) 2 , xϵ [-4,5; -7];

у = — (х-5) 2 , xϵ [4,5;7];

у = (2/9) х 2 +2, xϵ [-3;3].

Построить рисунок «Динозаврик» [5] по заданным уравнениям графиков функций:

у = (-1/8) х 2 +5, xϵ[ -5,2;4 ] ;

у = (-5/16) (х-8) 2 +8, xϵ[ 4;12 ] ;

у = -0,5 (х+7) 2 +3, xϵ [ -9; -5 ] ;

у = -0,5 (х-10) 2 +1, xϵ[ 8;12 ] ;

у = (х+3) 2 -7, xϵ [ -5; -1 ] ;

у = (х-4) 2 -7, xϵ[ 2;6 ] ;

у = (4/9) (х-0,5) 2 -4, xϵ[ -1;2 ] ;

у = 0,5(х-11) 2 -7, xϵ [9;13].

Построить рисунок «Верблюд» [5] по заданным уравнениям графиков функций:

у = -0,5х 2 +4, xϵ[ -2;2 ] ;

у = -0,5(х+4) 2 +4, xϵ [ -6; -2 ] ;

у = 0,5 (х-3) 2 +1,5, xϵ[ 2;6 ] ;

у = -0,5 (х-8) 2 +8, xϵ[ 6;10,5 ] ;

у = (х-9,5) 2 +4, xϵ[ 8,5;10,5 ] ;

у = -0,5(х-8,5) 2 +5, xϵ[ 4;8,5 ] ;

у = (1/8) (х+3) 2 -5, xϵ[ -7;1 ] .

у =-0,25 (х+6) 2 +2, x ϵ [ -11; -6 ] ;

у = 3 (х+6), xϵ [ -8; -7 ] ;

Выбранный для просмотра документ Карта проекта. Группа 1. Построение рисунков с помощью графиков.docx

по теме «Построение рисунков с помощью графиков функций»

Цель работы: применение навыков построения графиков.

Оборудование: шаблоны графиков функций, линейка, карандаш, «Учебное электронное издание математика 5-11».

Построить рисунок «Птица» по заданным уравнениям графиков функций:

у = (-4/27) х 2 +6, xϵ[0 ;9 ] ;

у = (1/9) (х-7) 2 -4, xϵ[ -2;7 ] ;

у = -0,5(х+2) 2 +8, xϵ[ -4;0 ] ;

у = (-1/16) (х+2) 2 +5, xϵ[ -6;2 ] ;

Распределить обязанности в группе:

А) представление теоретического материала по теме «Функция»;

Б) изготовление шаблонов парабол (уравнения №1-№4);

В) Заполнение таблицы №1 для построения рисунка;

Г) Построение рисунка с помощью шаблонов и линейки;

Д) Построение рисунка с помощью пособия «Учебное электронное издание математика 5-11»;

Е) Представление результатов работы в группе.

2. Выполнение работы:

2.1. Актуализация теоретических знаний по теме «Функция».

2.2. Изготовление шаблонов парабол

2.3. Заполнение таблицы №1

Вид графика (парабола, прямая)

Шаблон у=ах 2 , а

Ветви направлены (вверх, вниз)

2.4. Построение рисунка на координатной плоскости с помощью шаблонов и линейки.

2.5. Построение рисунка с помощью пособия «Учебное электронное издание математика 5-11».

3. Представление результатов работы группы.

Выбранный для просмотра документ Презентация. Построение рисунков с помощью графиков. Ржевская Диана, сош 31.pptx

Описание презентации по отдельным слайдам:

Выполнила РЖЕВСКАЯ ДИАНА ученица 9 А класса БОУ СОШ № 31 МО Динской район Руководитель проекта Баранова М.Н. учитель математики БОУ СОШ № 31 МО Динской район XXV районная научно-практическая конференция учащихся 9-11 классов Построение рисунков с помощью графиков функций

Графики живых организмов

Берёзовый долгоносик вырезает из листа колыбельку для своего детёныша в форме эволюты

Форму логарифмической спирали имеют: галактика, паутина паука, раковина улитки, рога козлов,…

Использование графиков в деятельности человека

Использование оптического свойства параболы

Всякий ли объект может быть описан с помощью уравнений графиков функций? Гипотеза:

Доказать, что любой объект можно описать с помощью уравнений графиков функций. Цель работы:

Изучение теоретического материала по темам «Графики функций», «Преобразования графиков функций». Построение рисунков по заданным уравнениям графиков функций. Описание рисунка «Черепашка» с помощью уравнений графиков функций. Проверка правильности выполнения практических заданий с помощью компьютерной программы «Учебное электронное издание, математика 5-11». Задачи:

Уравнение и график линейной функции: у=кх+в; график – прямая. Уравнение и график квадратичной функции: у=а(х-n)²+m; график – парабола. Преобразования графиков: перенос вдоль оси Ох и Оу. Поиск графиков, не изучаемых в школьном курсе. Изучение теоретического материала.

Трёх лепестковая роза . Лемниската Бернулли

Выполнение практической работы №1 «Построение рисунков с помощью графиков функций» и проверка её результатов с помощью компьютерной программы «Учебное электронное издание, математика 5-11». Построение рисунков по заданным уравнениям графиков функций.

1.у = (-4/27)х² +6, х є [0;9]; 2.у = (1/9)(х – 7)² — 4, х є [-2;7]; 3.у = -0,5(х + 2)² + 8,x є [-4;0]; 4.у = (-1/16)(х + 2)² +5, x є [-6;2]; 5.y = x + 10, x є [-6;-4]; 6.y = -x = 3, x є [7;9]; 7.y = 0.5x – 1, x є [-6;1]; 8.y = 0.5x – 2.5, x є [-5;2]. Задание №1. построить рисунок «Птица» по заданным уравнениям графиков функций:

Практическая работа №2 «Описание рисунка «Черепашка» с помощью уравнений графиков функций».

Найдем координаты точек А1 и В1 в системе координат О1х1у1 А1(-2,6;-1), В1(0;0) -1,3=а*(-2,6)2 -1=а*6,76 а=-1/6,76=-100/676=-50/338=-25/169 у=-25/169 х2 Найдем координаты вершины В1 в системе координат Оху (9;11,8) у=-25/169(х-9)2+11,8 Промежуток [6,4; 10,8] Фрагмент рисунка напоминает параболу.

Этот участок напоминает прямую. А2(х2;у2) ; А4(х4;у4) А2(14,6; 6,8) ; А4(14,9; 6) у=(х-х2)(у4-у2)/(х4-х2)+у2 у=(х-14,6)(6-6,8)/(14,9-14,6)+6,8 Промежуток [14,6; 14,9] Фрагмент рисунка А2А4

С помощью программы «Учебное электронное издание математика 5-11 » получен рисунок «Черепашка».

Вывод: Любой объект можно описать с помощью уравнений графиков функций.

ученными было установлено, что с помощью математических уравнений можно описать движение животного (кошки). Почти 40 лет назад, 1968 год… Группа под руководством Николая Николаевича Константинова создает математическую модель движения животного (кошки).Машина БЭСМ-4, выполняя написанную программу решения обыкновенных (в математическом смысле слова) дифференциальных уравнений, рисует мультфильм «Кошечка», содержащий даже по современным меркам удивительную анимацию движений кошки, созданную компьютером. При изучении теоретического материала, я узнала, что

Выбранный для просмотра документ Проектная работа. Построение рисунков. Ржевская Диана. сош 31.docx

XXV районная научно-практическая конференция

школьников Динского района

Построение рисунков с помощью графиков функций.

ученица 9а класса

МО Динской район.

МО Динской район

к работе по теме «Построение рисунков с помощью графиков функций» ученицы 9а класса БОУ СОШ №31 МО Динской район

Тема работы «Построение рисунков с помощью графиков функций» для школы актуальна. В работе раскрывается проблема: можно ли описать окружающие нас объекты с помощью графиков функций?

Цель работы: описать рисунок «Черепашка» с помощью уравнений графиков функций.

Для этого ученицей изучен теоретический материал по темам «Графики элементарных функций», «Преобразования графиков функций». Найден дополнительный иллюстративный материал по теме работы.

Цель практической работы №1 – отработка навыков построения графиков. Её выполнение позволило ученице применить свои теоретические знания на практике при построении рисунков.

В практической работе №2 Диана самостоятельно описала рисунок «Черепашка» с помощью уравнений графиков функций (линейной и квадратичной). Проверила правильность выполнения всех заданий практических работ с помощью программы «Учебное электронное издание математика 5-11» /Дрофа –ДОС для НФПК/.

Цель работы достигнута. Рисунок «Черепашка» описан с помощью графиков функций. Сделан вывод о том, что при выполнении рисунка достаточно использовать лишь линейные функции.

Учитель математики БОУ СОШ №31

МО Динской район М.Н. Баранова

Практическая работа №1 «Построение рисунков с помощью графиков функций»……………………………………………………………..5

3. Практическая работа №2 «Создание рисунка «Черепашка» и описание его с помощью уравнений графиков функций»………………………………8

Е) Приложение №6 (шаблоны графиков функций)………………………27

Функция – это одно из основных математических понятий, выражающее зависимость между переменными [1].

График функции – это один из способов представления функции. Представить какую-либо функцию можно разными способами. Например, табличным или графическим [1].

Табличный способ предпочитают тогда, когда трудно вычислять значения функции [1].

Графический способ представления функции – самый наглядный. График функции – это линия, дающая цельное представление о характере изменения её уравнения [1].

В школьной программе мы изучаем самые простейшие графики и их преобразования.

Помимо графиков функций, изучаемых нами в школе, существую и другие, интересные и «красивые» графики. Например, кардиоида, астроида, декартов лист, лемниската Бернули, спираль Архимеда и другие (Приложение №1) [2].

Живая природа демонстрирует нам многочисленные графики живых организмов. Например, березовый долгоносик, изготовляя колыбельку для своего детёныша, на листке вырезает эволюту. Паук плетёт паутину, которая выглядит как логарифмическая спираль [3].

Если взглянуть на форму многих галактик, то можно обнаружить, что некоторые из них имеют форму логарифмической спирали. Галактика млечный путь – типичная спиральная галактика [3]. (Приложение 2).

Но форму логарифмической спирали имеют не только объекты астрономии, но и, например: рога козлов, паутина, ракушки многих улиток, расположение семечек в цветке подсолнуха. Так же широкое применение нашла логарифмическая спираль в экономике [3].

Так же было установлено, что с помощью математических уравнений можно описать движение. Так, существуют математические уравнения колебания струны, математического маятника и другие.

Почти 40 лет назад, 1968 год… группа под руководством Николая Николаевича Константинова создает математическую модель движения животного (кошки). Машина БЭСМ -4, выполняя написанную программу решения обыкновенны (в математическом смысле слова) дифференциальных уравнений, рисует мультфильм «Кошечка» (Приложение№3), содержащий даже по современным меркам удивительную анимацию движений кошки, созданную компьютером.

В этой работе рассматриваются различные элементарные функции. Работа включает в себя две практические работы: «Построение рисунков с помощью графиков функций», «Создание композиции «Черепашка» и описание её с помощью уравнений графиков функций».

Я представляю два варианта выполнения рисунков: ручной и электронный. Электронный вариант осуществлён с помощью программы «Учебное электронное издание математика 5-11».

Цель этих практических работ: применение навыков построения, преобразования графиков функций при создании рисунков и применение навыков преобразования графиков функций при составлении композиции.

Практическая работа №1

Тема: «Построение рисунков с помощью графиков функций».

Цель работы: применение навыков построения графиков.

Оборудование: шаблоны графиков функций, линейка, карандаш, «Учебное электронное издание математика 5-11».

Построить рисунок «Птица» [4] по заданным уравнениям графиков функций: