Резонансный случай в дифференциальных уравнениях

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Резонансный случай в дифференциальных уравнениях

Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:
P_k(x)exp(ax)cos(bx) + Q_m(x)exp(ax)sin(bx),
где P_k(x), Q_m(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.

Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.
Искомое решение уравнения записывается в виде:
(P_r(x)exp(ax)cos(bx) + Q_r(x)exp(ax)sin(bx))x s ,
где P_r(x), Q_r(x) — многочлены степени r = max(k, m) с неизвестными коэффициентами
p_r , p_r-1, . p₁, p₀, q_r, q_r-1, . q₁, q₀.
Сомножитель x s называют резонансным сомножителем. Резонанс имеет место в случаях, когда среди корней характеристического уравнения есть корень
l =a ± ib кратности s.
Т.е. если среди корней характеристического уравнения соответствующего однородного уравнения есть такой, что его действительная часть совпадает с коэффициентом в показателе степени экспоненты, а мнимая — с коэффициентом в аргументе тригонометрической функции в правой части уравнения, и кратность этого корня s, то в искомом частном решении присутствует резонансный сомножитель x s . Если же такого совпадения нет (s=0), то резонансный сомножитель отсутствует.

Подставив выражение для частного решения в левую часть уравнения, получим обобщенный многочлен того же вида, что и многочлен в правой части уравнения, коэффициенты которого неизвестны.
Два обобщенных многочлена равны тогда и только тогда, когда равны коэффициенты при сомножителях вида x t exp(ax)sin(bx), x t exp(ax)cos(bx) с одинаковыми степенями t.
Приравняв коэффициенты при таких сомножителях, получим систему 2(r+1) линейных алгебраических уравнений относительно 2(r+1) неизвестных. Можно показать, что такая система совместна и имеет единственное решение.

ПРИМЕР 1. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен. Резонанса нет.

ПРИМЕР 2. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен. Резонанс есть.

ПРИМЕР 3. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен, умноженный на экспоненту. Резонанса нет.

ПРИМЕР 4. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен, умноженный на экспоненту. Резонанс есть.

ПРИМЕР 5. Решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части обобщенный многочлен.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

научная статья по теме АСИМПТОТИКИ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ВЫРОЖДЕНИЯМИ В СЛУЧАЕ РЕЗОНАНСА Математика

Цена:

Авторы работы:

Научный журнал:

Год выхода:

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Текст научной статьи на тему «АСИМПТОТИКИ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ВЫРОЖДЕНИЯМИ В СЛУЧАЕ РЕЗОНАНСА»

ДОКЛАДЫ АКАДЕМИИ НАУК, 2013, том 449, № 3, с. 259-262

АСИМПТОТИКИ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ВЫРОЖДЕНИЯМИ В СЛУЧАЕ РЕЗОНАНСА © 2013 г. М. С Волнухин

Представлено академиком В.А. Ильиным 03.10.2012 г.

Поступило 16.10.2012 г.

Работа посвящена исследованию асимптотических разложений вырожденных эллиптических уравнений в резонансном случае, а именно, уравнений вида

ласть комплексной плоскости Сх. Пространство

Е( 1 ) — пространство голоморфных на 1 я>Е функций, имеющих не более чем экспоненциальный рост на бесконечности, т.е.

Аналогично определяется пространство Е(С) — пространство голоморфных на Е(С) функций, имеющих не более чем экспоненциальный рост на бесконечности.

В работах [4, 1] показано, что можно построить преобразование Бореля—Лапласа

определяющее взаимно-однозначное соответствие в пространствах Е( Е) ^ Е( )/Е(С).

Здесь у — граница области 1я>Е (изображение соответствующего контура можно найти в [1]).

Определение 1. Функция g называется бесконечно продолжи мой, если для любого действительного числа Я > 0 существует дискретное множество ZR е С, что функция g анали-

тически продолжается из первоначальной области определения вдоль любого пути длины У

С — соответствующие кон-

Назовем т, кратностью соответствующего обобщенного ВКБ-элемента. Как видно из формулировки теоремы, кратность каждого элемента решения, вообще говоря, на единицу больше кратности соответствующего элемента правой части (6). Это объясняет то, почему в резонансном случае уравнение не является замкнутым относительно суммы обыкновенных ВКБ-элементов (2).

В зависимости от вида слагаемых (2) можно выделить случаи сильного и слабого резонанса (см. определение ниже). В случае сильного резо-

АСИМПТОТИКИ РЕШЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

нанса рост кратности происходит, в случае слабо-

го — нет. Пусть Н1(р) = Н( г-р ) — 00 ,р )

рень линейного уравнения Н1(рр) — ХрН1(рр)’, р = 1, 2, . п. Этот параметр влияет на величины констант ар, С’, Б,’ в асимптотике решения (см. формулировку теоремы 1).

О п р е д е л е н и е 3. Для правой части уравнения (1) с асимптотикой

/(г) = £еггь£I £гЧп’г + £ вуг 1пг

назовем сильным резонансом случай, когда хотя бы для одногор е выполнено Тр — Хр е Z и при этом Тр — Хр + кт ‘ — 1 по теме «Математика»

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Вынужденные колебания

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Видео:Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.

Видео:Дифференциальные уравнения. 11 класс.Скачать

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($_r$) равна:

При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:

где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Примеры задач с решением

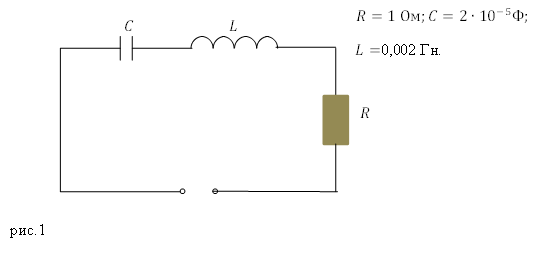
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

🌟 Видео

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Классические уравнения | резонанс в простейшем случаеСкачать

Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Поле направлений дифференциального уравнения первого порядкаСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения для самых маленькихСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать