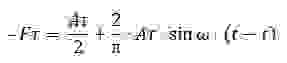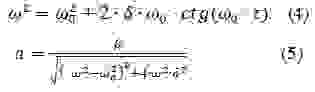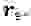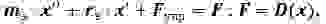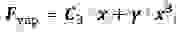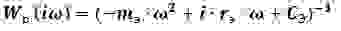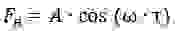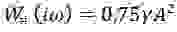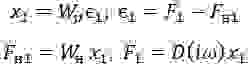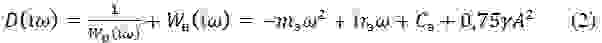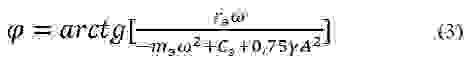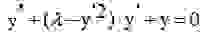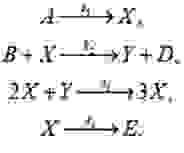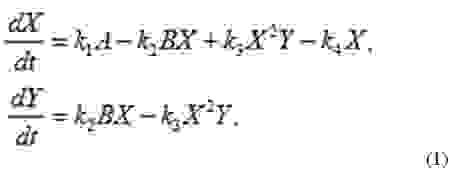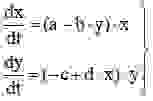Резонанс в дифференциальных уравнениях пример (5 видео)

Резонанс в дифференциальных уравнениях пример

Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:
P_k(x)exp(ax)cos(bx) + Q_m(x)exp(ax)sin(bx),
где P_k(x), Q_m(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.

Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.
Искомое решение уравнения записывается в виде:
(P_r(x)exp(ax)cos(bx) + Q_r(x)exp(ax)sin(bx))x s ,
где P_r(x), Q_r(x) — многочлены степени r = max(k, m) с неизвестными коэффициентами
p_r , p_r-1, . p₁, p₀, q_r, q_r-1, . q₁, q₀.
Сомножитель x s называют резонансным сомножителем. Резонанс имеет место в случаях, когда среди корней характеристического уравнения есть корень
l =a ± ib кратности s.
Т.е. если среди корней характеристического уравнения соответствующего однородного уравнения есть такой, что его действительная часть совпадает с коэффициентом в показателе степени экспоненты, а мнимая — с коэффициентом в аргументе тригонометрической функции в правой части уравнения, и кратность этого корня s, то в искомом частном решении присутствует резонансный сомножитель x s . Если же такого совпадения нет (s=0), то резонансный сомножитель отсутствует.

Подставив выражение для частного решения в левую часть уравнения, получим обобщенный многочлен того же вида, что и многочлен в правой части уравнения, коэффициенты которого неизвестны.
Два обобщенных многочлена равны тогда и только тогда, когда равны коэффициенты при сомножителях вида x t exp(ax)sin(bx), x t exp(ax)cos(bx) с одинаковыми степенями t.
Приравняв коэффициенты при таких сомножителях, получим систему 2(r+1) линейных алгебраических уравнений относительно 2(r+1) неизвестных. Можно показать, что такая система совместна и имеет единственное решение.

ПРИМЕР 1. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен. Резонанса нет.

ПРИМЕР 2. Частное решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен. Резонанс есть.

ПРИМЕР 3. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен, умноженный на экспоненту. Резонанса нет.

ПРИМЕР 4. Общее решение линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части многочлен, умноженный на экспоненту. Резонанс есть.

ПРИМЕР 5. Решение задачи Коши для линейного неоднородного дифференциального уравнения с постоянными коэффициентами. В правой части обобщенный многочлен.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Содержание

Вынужденные колебания
Определение вынужденных колебаний
Дифференциальное уравнение вынужденных колебаний
Резонанс вынужденных колебаний
Примеры задач с решением
Автоколебания и резонанс
Здравствуйте!
Автоколебания в технике
Химические колебания. Брюсселятор
Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)
📽️ Видео

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Вынужденные колебания

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Определение вынужденных колебаний

Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.

Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС), называют вынужденными механическими (электромагнитными) колебаниями.

Видео:Дифференциальные уравнения: пример 1Скачать

Дифференциальное уравнение вынужденных колебаний

Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:

Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:

где $x$ — координата; $delta $ — коэффициент затухания; $_0$ — циклическая частота свободных незатухающих колебаний (если $delta $=0, то $_$называют собственной частотой колебаний).

Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:

где $q$ — заряд; $delta =frac$ — коэффициент затухания; $_0=frac<sqrt>$; $U=U_m$ — внешнее переменное напряжение.

Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:

где $s$ — колеблющийся параметр; $x_0=frac$ если колебания механические ($x_0=frac— в случае электрических колебаний$).

Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:

Его общее решение:

где $A_0$ — начальная амплитуда колебаний.

Частное решение уравнения (4) в представлено выражением:

Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).

Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Резонанс вынужденных колебаний

Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.

Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac$ и приравняв ее к нулю получим:

Равенство (10) справедливо при:

Получается, что резонансная частота ($_r$) равна:

При $^2ll ^2_0$ резонансная частота совпадает с собственной частотой колебаний $_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:

При небольшом затухании колебаний (если $^2ll ^2_0$) амплитуда при резонансе равна:

где $Q=frac<_0>$ — добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Примеры задач с решением

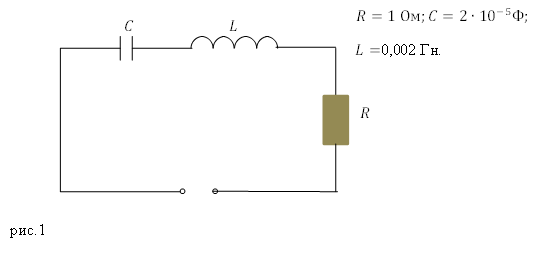
Задание. Какова добротность колебательного контура, представленного на рис.1?

Решение. Добротность электрического колебательного контура найдем как:

При этом собственная частота колебаний в таком контуре равна:

коэффициент затухания находим как:

Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:

Ответ. $Q=10$

Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать колебания сила $F=$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?

Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний будет выражение:

где коэффициент затухания равен $delta =frac$. Из функции, которая задает вынуждающую силу:

мы видим, что амплитуда силы равна единице:

Собственная частота колебаний груза на пружине:

Амплитуда при резонансе таких колебаний равна:

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Автоколебания и резонанс

Здравствуйте!

В связи с вопросами читателей моей публикации [1] касательно условий возбуждения автоколебаний в механической системе, я решил описать явление возникновения и поддержания автоколебаний подробно, выделив основные области возникновения и применения автоколебаний.

В википедии автоколебания объясняют так [2]:

Незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. При этом частота становится почти равной резонансной.

Автоколебания в технике

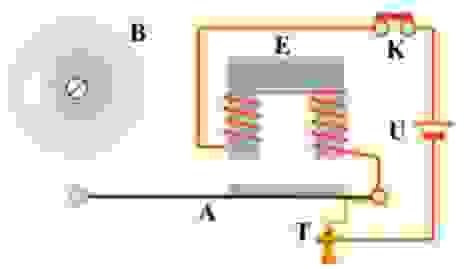
Автоколебательная система с запаздыванием (на примере электромеханического звонка)
Приведём пример электромеханического звонка:

При замыкании цепи кнопкой (К) электромагнит (Е) притягивает ударник, ударник бьёт по звонку и размыкает цепь питания электромагнита, механически связанным с ним контактом (Т) ударник (А) возвращается назад и процесс повторяется.

При рассмотрении процесса возникновения автоколебаний будем считать, что сила, действующая на боёк (А) звонка, изменяется пропорционально изменению тока в RL цепи.

Такое допущение сделано для упрощения рассмотрения, поскольку зависимость силы от тока в обмотке и зазора между бойком и полюсами значительно сложнее [3].

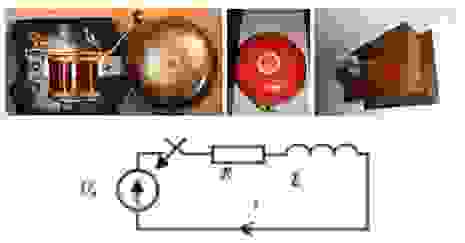
Ниже приведены конструкции электромеханических звонков и их упрощённая электрическая схема:

Боёк колеблется относительно установленного зазора согласно соотношению A*sin (w*t).
Решив численным методом дифференциальное уравнение RL цепи с начальными условиями
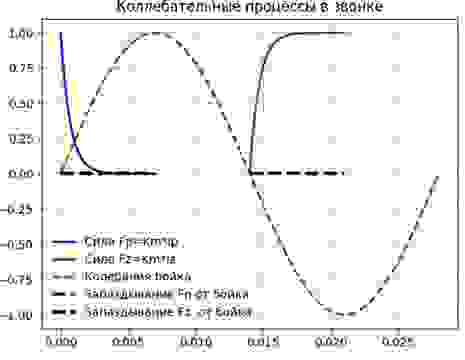
для замыкания и размыкания контакта, наложив на эти решения колебания бойка, получим:

Для приближенной теории будем считать, что сила Fτ, выраженная последовательностью прямоугольных импульсов, которые возникает и исчезает мгновенно, но не в момент срабатывания контакта, а с запаздыванием τ=L/R. Добавим Fτ на график, получим:

Обозначим амплитуду силы Fτ через Aτ, получим разложения этой силы в ряд Фурье [4] (учитывая что x=a∙sin(ω∙t), для первых двух членов ряда:

Будем считать, что постоянная составляющая силы Aτ/2 компенсируется регулировкой.
Тогда уравнение для колебаний бойка с учётом его приведенной массы m, трения r и изгибной жёсткости k примет вид:

(1)

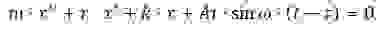
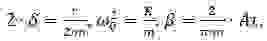
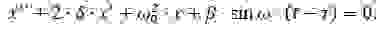
Разделим обе части на массу бойка, введем обозначения, получим:

(2)

Для того, чтобы получить аналитические соотношения для частоты и амплитуды колебаний бойка, решим (2) приближённым методом [5]. Преобразуем (2) к виду:

(3)

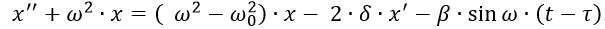
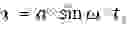
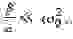
Подставив в (3) при условии:
пропуская промежуточные выкладки получим соотношения для частоты и амплитуды автоколебаний:

На основании приведенных соотношений можно сделать вывод, что, при отсутствии самоиндукции, звонок работать не может, поскольку при L=0 нет запаздывания τ=0. Таким образом, при нулевом запаздывании автоколебания не возможны.

Автоколебания в измерительной технике (на примере механического резонатора вибрационных плотномеров)

Механические резонаторы в виде трубок пластин или цилиндров широко используются в вибрационных плотномерах, внешний вид которых приведен на рисунках:

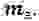
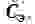
Будем рассматривать резонатор c сосредоточенными эквивалентными параметрами: массой жесткостью и трением, характеризуемым коэффициентом

Такая замена вполне допустима в ограниченной области частот при соблюдении равенства собственных частот колебаний обеих систем, а также равенства потерь энергии и обусловленных ими затуханий.

Запишем систему уравнений, описывающих движение резонатора в замкнутой системе возбуждения:

где: F- сила воздействия системы возбуждения на резонатор;
D(x)- неизвестный оператор обратной связи, подлежащий определению; Fупр — упругая восстанавливающая сила резонатора, которая в общем случае может описываться нелинейной функцией; х — поперечное смещение эквивалентной массы.

Воспользуемся выражением кубической упругой характеристики резонатора:

где γ — коэффициент, характеризующий отклонение реальной упругой характеристики от линейной.

Преобразуем записанную систему равенства к виду:

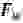
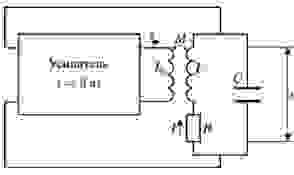
где — нелинейная составляющая упругой силы.

Структурная схема автоколебательной системы, работа которой характеризуется уравнениями, (1) приведена на рисунке:

Схема содержит нелинейное звено, выполняющее функцию корректирующей обратной связи линейного резонатора, имеющего частотную характеристику:

Для решения задачи синтеза оптимальной системы возбуждения, воспользуемся методом гармонической линеаризации [6].

Механические резонаторы являются высокодобротными колебательными системами, которые можно рассматривать как узкополосные фильтры с выходным сигналом вида: x

A∙cos⁡(ω∙τ), где A— амплитуда колебаний резонатора; ω — частота колебаний, близкая к резонансной [7].

Поэтому для нелинейного элемента справедливо соотношение:

Пренебрегая третьей гармоникой, отфильтрованной линейной частью резонатора, частотную характеристику линеаризованного звена нелинейной упругости механического резонатора можно в виде:

Рассмотрим уравнение для первой гармоники колебаний линеаризованной системы:

Для определения вида частотной характеристики D(iω), обеспечивающей совместность этой системы, исключим промежуточные переменные прямой подстановкой их выражений через другие переменные. В результате получим:

Из соотношения (2) определим смещение фазы, осуществляемое системой возбуждения:

Нетрудно установить, что частота автоколебаний не будет зависеть от трения 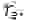при сдвиге фазы φ=π/2, тогда:

При этом условии из (2) следует, что система возбуждения должна быть дифференцирующим звеном D(iω)=(i*rэ* ω) т.е.

Из (5) следует, что частотная характеристика цепи обратной связи системы возбуждения должна быть пропорциональна коэффициенту трения

Система возбуждения состоит из трех элементов, D(iω)=Dп* Dу* D(в ), характеризующих частотные характеристики: приемника Dп, усилителя Dу и возбудителя D(в ) колебаний. Приемник является дифференцирующим – Dп=Kп* i*ω, а возбудитель усилительным
звеном – Dв=Kв.

Для выполнения условия (5) усилитель должен иметь частотную характеристику:

Коэффициент усиления должен меняться вместе с изменением трения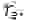
Звено с переменным коэффициентом усиления можно реализовать простейшей нелинейностью типа двухпозиционного реле, имеющей частотную характеристику по первой гармонике [6]:

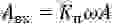
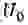
где — амплитуда первой гармоники на входе усилителя; — выходное напряжение усилителя, подаваемое на возбудитель колебаний.

Из (6) и (7) можно получить выражение для амплитуды установившихся автоколебаний резонатора:

Для устранения этого влияния амплитуды на частоту резонатора можно стабилизировать амплитуду A варьированием напряжения U0 с помощью регулятора, стабилизирующего амплитуду входного сигнала Aвх, поступающего с приемника колебаний.

Из изложенного можно сделать вывод, что частота автоколебаний резонатора вибрационного измерительного преобразователя не будет зависеть от трения при сдвиге фазы φ=π/2, когда система возбуждения является дифференцирующим звеном, и не будет зависит от амплитуды автоколебаний при стабилизации входного сигнала этого звена.

Автоколебания в радиотехнических генераторах (на примере решения уравнения
Ван-дер-Поля)

Обобщённая схема радиотехнического генератора автоколебаний приведена на рисунке:

Механизм возбуждения автоколебаний в генераторе можно качественно описать следующим образом. Даже при отсутствии напряжения на выходе усилителя напряжение в контуре испытывает случайные флуктуации. Они усиливаются усилителем и вновь поступают в контур через цепь обратной связи.

При этом из шумового спектра флуктуаций будет выделяться составляющая на собственной частоте высокодобротного контура. Если энергия, вносимая в контур таким образом, превосходит энергию потерь, амплитуда колебаний нарастает.

Основной моделью, описывающей автоколебания в радиотехническом генераторе, является уравнение Ван-дер-Поля. Приведём уравнение Ван-дер-Поля к виду, содержащему единственный управляющий параметр с безразмерными переменными:

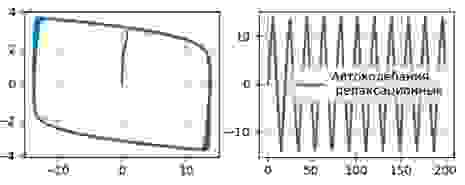
Получим фазовые портреты (слева) и временные реализации колебаний (справа) осциллятора Ван-дер-Поля: λ =0.1, λ =1.1

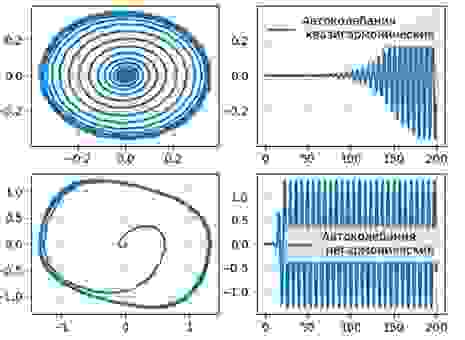
Для λ =10.0

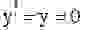
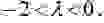
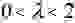
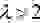
Уравнение Ван-дер-Поля имеет единственную особую точку , которая является устойчивым узлом при устойчивым фокусом при неустойчивым фокусом при и неустойчивым узлом при . Если выполнено условие самовозбуждения, на фазовой плоскости имеется также предельный цикл, отвечающий режиму периодических автоколебаний.

Химические колебания. Брюсселятор

Важным и нетривиальным примером автоколебательных процессов служат некоторые химические реакции. Химические колебания — это колебания концентраций реагирующих веществ.

К настоящему времени известно достаточно много колебательных реакций. Наиболее знаменитая из них была открыта Б.П. Белоусовым в 1950 г. и позднее детально изучена А.М. Жаботинским. Реакция Белоусова — Жаботинского (БЖ) представляет собой процесс окисления малоновой кислоты при взаимодействии в присутствии ионов в качестве катализатора.

В ходе реакции раствор периодически изменяет свой цвет: голубой — красный — голубой — красный и т.д. Кроме простых периодических колебаний, реакция БЖ демонстрирует (в зависимости от условий эксперимента) множество различных типов пространственно-временной динамики, которые окончательно еще не исследованы.

Предложены различные математические модели реакции БЖ (например, модель Филда, Кереса и Нойеса — «орегонатор»), однако ни одна из них не описывает полностью все детали, наблюдаемые в эксперименте.

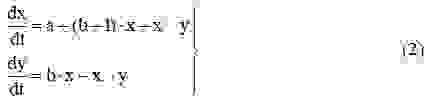
Мы рассмотрим более простой модельный пример: гипотетическую химическую реакцию, которая получила название Брюсселятор [8]. Уравнения этой реакции имеют вид:

Предполагается, что реагенты A и B имеются в избытке, так что их концентрации можно считать постоянными, а D и E ни в какие реакции не вступают. Составим кинетические уравнения, соответствующие реакции, которые описывают динамику концентраций реагирующих веществ.

Поскольку число актов химической реакции в единицу времени определяется вероятностью столкновения молекул реагентов, скорости изменения концентраций продуктов реакции пропорциональны произведению концентраций соответствующих реагентов с коэффициентами пропорциональности, называемыми константами скоростей реакций. Тогда кинетические уравнения можно записать в виде:

Символами Y,X будем теперь обозначать соответствующие концентрации. Отметим, что из третьего уравнения системы следует, что скорость образования вещества X зависит от его концентрации, т.е. эта стадия реакции носит автокаталитический характер. Приведем уравнения (1) к безразмерному виду, содержащему минимальное число управляющих параметров. Для этого перейдём к новым переменным, Тогда уравнения (1) примут вид:

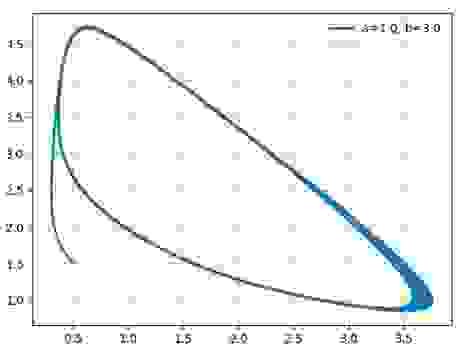
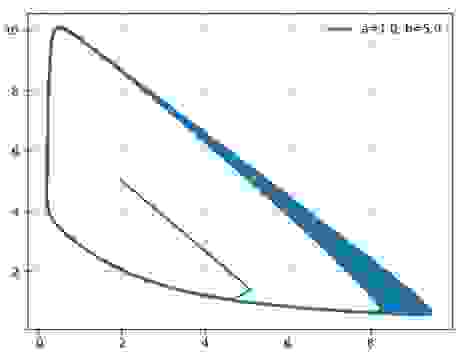
Построим фазовые портреты для: a=1.0; b=2.1; b=3.0;b=5.0

Таким образом, химический осциллятор демонстрирует поведение, типичное для автоколебательных систем и вполне аналогичное, например, осциллятору Ван-дер-Поля.

Автоколебания в биосистемах (на примере модели Лотки Вольтерра –“Хищник -жертва”)

В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка.

Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть x и y— число жертв и хищников соответственно. Предположим, что относительный прирост жертв y’/x равен a-by, a>0, b>0, где a — скорость размножения жертв в отсутствие хищников, -by— потери от хищников.

Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x=0 ) относительная скорость изменения популяции хищников равна y’/y =-c, c>0, наличие пищи компенсирует убывание, и при x>0 имеем y’/y =(-c +d*x), d>0.

Таким образом, система Вольтерра—Лотка имеет вид:

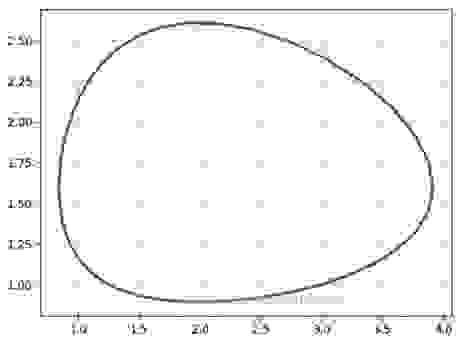
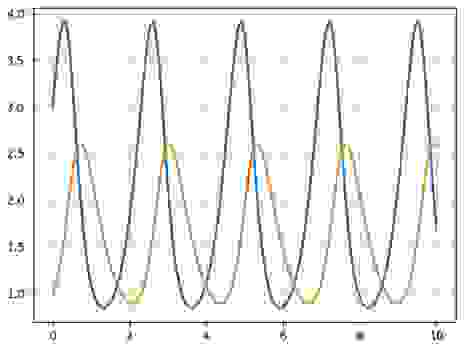
Рассмотрим фазовый портрет системы Вольтерра Лотка, для a=4 b=2.5, c=2, d=1 и графики ее решения с начальным условием x(0)=3, y(0)=1, построенные программой Python для численного решения системы обыкновенных дифференциальных уравнений:

Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1, обе популяции сначала растут. Когда число хищников достигает величины b=2.5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать.

Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x=c/d =2 (в этой точке y’=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины y=a/b =1.6 (в этой точке x’=0).

С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и… процесс повторяется снова и снова.

Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.