Решите уравнение sin2x корень из 3sinx

Условие

а) Решите уравнение sin2x+sqrt(3)sinx=0.

б) Найдите все корни этого уравнения, принадлежащие отрезку [5π/2 ; 7π/2].

Решение

Все решения

По формуле синуса двойного угла
sin2x=2*sinx*cosx

sinx=0 или 2cosx+sqrt(3)=0
x=πk, k∈Z или сosx=-sqrt(3)/2
x=± arccos(-sqrt(3)/2)+2πn, n∈Z
x=± (π- arccos sqrt(3)/2)+2πn, n∈Z
x=± (π- (π/6))+2πn, n∈Z
x=± (5π/6))+2πn, n∈Z

О т в е т. а)πk; ± (5π/6))+2πn, k, n∈Z

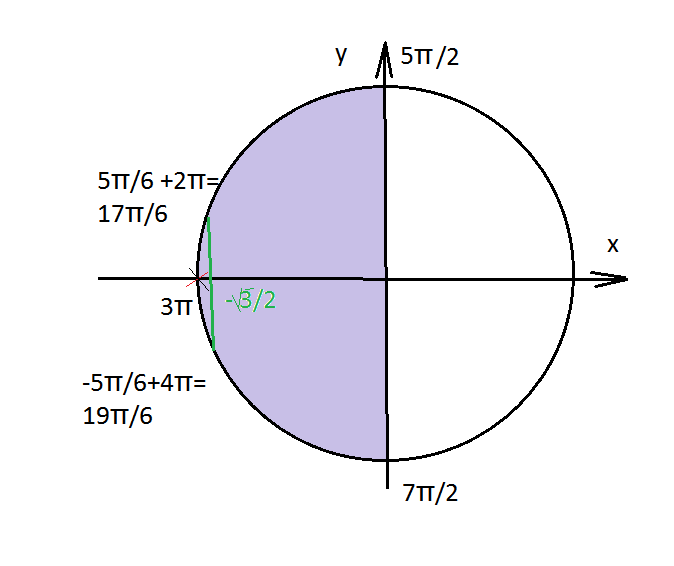
б) Найдем корни, принадлежащие отрезку [5π/2 ; 7π/2].
Для этого составим неравенство
5π/2

Видео:Математика а) Решите уравнение Sin2x-2√3 (Sinx)^2+4Cosx-4√3 Sinx=0 б) Найдите все корни этогоСкачать

А) Ре­ши­те урав­не­ние sin2x+√3sinx=0. б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку [5П/2;7П/2].

2sinxcosx+√3sinx=0
sinx(2cosx+√3)=0
sinx=0⇒x=πn x=3π∈[5π/2;7π/2]
cosx=-√3/2⇒x1=5π/6+2πn
x=17π/6∈[5π/2;7π/2] U x2=-5π/6+2πn x=19π/6∈[5π/2;7π/2]

Если ответ по предмету Алгебра отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Видео:Простая тригонометрия min(cosx-sqrt(3)sinx)Скачать

Немного теории.

Видео:Математика а) Решите уравнение 2Sin2x+2√3 Sinx=2Cosx+√3 б) Укажите корни этого уравненияСкачать

Тригонометрические уравнения

Видео:Математика а) Решите уравнение 2Sin2x –Cosx = √3Sinx б) Найдите все корни этого уравненияСкачать

Уравнение cos(х) = а

Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если a

Видео:Реальный ЕГЭ-2022, профильная математика, задача 12: sin2x-2sin(-x)-cos(-x)-1=0.Скачать

Уравнение sin(х) = а

Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac; ; frac right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если а

Видео:Тригонометрические уравнения sin2x=√2/2; cos x/3=-1/2Скачать

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале ( left( -frac; ; frac right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right) ); если а

Видео:Математика а) Решите уравнение (1-Cos2x)Sin2x = 3^(1/2) (Sinx)^2 б) Укажите корни этого уравненияСкачать

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Видео:3C Решите уравнение: 4*cos(2x)+3*sin^2 (x) = cos^2 (x) - 4*sin(x)Скачать

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac + pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac + pi n, ; n in mathbb )

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Видео:простейшие уравнения с sinx: 1)sinx=√2/2; 2)sinx=-√3/2Скачать

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы ( sin(x) = 2sinfrac cosfrac, ; cos(x) = cos^2 frac -sin^2 frac ) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac + cos^2 frac right) ) получаем

Поделив это уравнение на ( cos^2 frac ) получим равносильное уравнение ( 3 text^2frac — 4 textfrac +1 = 0 )
Обозначая ( textfrac = y ) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:

Видео:Тригонометрические уравнения 2sin(3x-П/4)=-корень из 2; корень из 3tg(x/4 +П/6)=3Скачать

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0

💥 Видео

Математика а) Решите уравнение (2Sin^2 X-3SinX+1)(tgX)^0.5=0 б) Укажите корни этого уравненияСкачать

а) Решите уравнение √3/4sinx(cosx-√2)=(√2cosx-cos²x)sin²x. б) Укажите корни этого уравненияСкачать

Математика Дано уравнение 2ctg^2 x +3/Sinx =0 а) Решите уравнение б) Найдите его корниСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Решите уравнение sin(πx/3) = 1/2 В ответе напишите наименьший положительный корень.Скачать

Математика Решите уравнение Cos3x -Sinx = √3(Cosx -Sin3x)Скачать

ЕГЭ 2020 Математика C1 №3 Решение тригонометрического уравнения, исследование ОДЗ [МИФ]Скачать

Решите уравнение ➜ sin⁡x+cos⁡x=1 ➜ 2 способа решенияСкачать