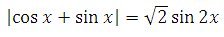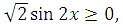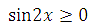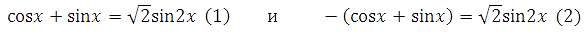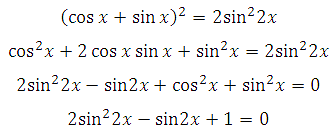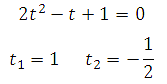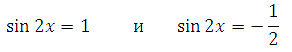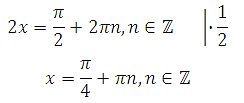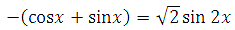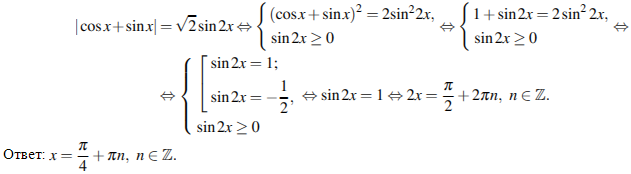Решите уравнение модуль cosx sinx корень из 2 sin2x

1. Сразу следует отметить, что выражение

так как |cos x+sin x| имеет неотрицательное значение. Исходя из того, что корень из двух есть число положительное, получаем:

2. Используя свойство модуля, получим два уравнения, решения каждого из них будут являться решением данного уравнения:

Решаем первое. Возводим в квадрат обе части:

Данное уравнение сводится к квадратному . Пусть sin2x = t, тогда получим

Мы установили (в начале решения), что sin2x ≥ 0. Это область допустимых значений. Можем сделать вывод, что второе уравнение решать нет смысла – так как полученные при решении значения х не будут входить в область определения.

Решаем sin2x = 1, получим:

Рассмотрим второе уравнение:

Решением является тот же корень что и при решении уравнения (1), так как при возведении в квадрат обеих частей получим то же уравнение

Видео:Математика а) Решите уравнение |Cosx+Sinx|=√2 Sin2x. б) Найдите решение уравнения, принадлежащиеСкачать

Задача 1797 Решите |cosx+sinx| = sqrt(2)sin2x.

Условие

Решите |cosx+sinx| = sqrt(2)sin2x

Решение

Ответ: Pi/4+Pin

Как мы перешли к sin2x=1 и sin2x=-1/2?

В выражение 1+sin2x = 2sin^22x замените sin2x = t. Решите уравнение 1+t = 2t^2. У вас получатся корни t=1 и t=-1/2. Перейдите к обратное замене sin2x=1 и sin2x=–1/2

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрические уравнения с модулем

Разделы: Математика

Раскрытие модуля по определению

Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0

sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)

Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2

cosx=0 или x+1,5=1 или x-1,5 = -1

х= -0,5 х = -2,5

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)

Ответ:

№5. Найти все решения уравнения на отрезке [0;4].

Решение. Перепишем уравнение в виде

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим

Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии

Решая вторую систему, получим систему , которая не имеет решений.

Ответ:

№6 Решить уравнение.

Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:

х=2

Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2

№7. Решить уравнение.

Решение. ОДЗ:

Раскрывая знак модуля, получаем системы:

Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида

Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.

Ответ:

№8. Решить уравнение.

Решение. Преобразуем уравнение следующим образом:

Ответ:

№9. Решить уравнение.

Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.

Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1

при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.

При решении уравнения второй системы получается:

В промежутке только одно целое нечетное число 3, т.е

Другие способы раскрытия модулей.

Уравнения вида можно решать и следующим способом:

№10. Решить уравнение.

Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx 21.02.2008

💡 Видео

Решите уравнение ➜ sin⁡x+cos⁡x=1 ➜ 2 способа решенияСкачать

Реальный ЕГЭ-2022, профильная математика, задача 12: sin2x-2sin(-x)-cos(-x)-1=0.Скачать

Математика а) Решите уравнение Sin2x +√3(Cosx-Sinx) = 1.5 б) Укажите корни этого уравненияСкачать

Математика а) Решите уравнение Sin2X +2SinX = 1 + CosX б) Укажите корни этого уравненияСкачать

Тригонометрические уравнения sin2x=√2/2; cos x/3=-1/2Скачать

4 способа решить уравнение sinx = cosxСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

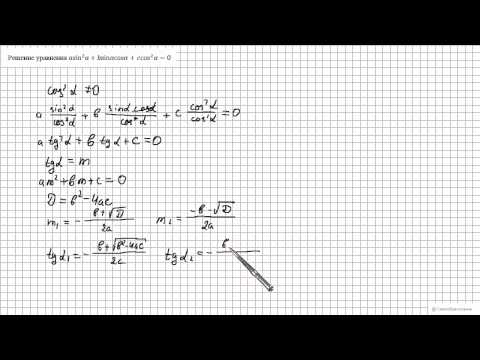
Решение уравнения a*sin^2(x)+b*sin(x)*cos(x)+c*cos^2(x)=0Скачать

Решаем уравнение: cos2x-sin2x=cosx+sinx+1Скачать

Простейшее тригонометрическое уравнение sin x = Корень из 2 /2Скачать

Математика а) Решите уравнение 2Sin2x –Cosx = √3Sinx б) Найдите все корни этого уравненияСкачать

Математика а) Решите уравнение (1-Cos2x)Sin2x = 3^(1/2) (Sinx)^2 б) Укажите корни этого уравненияСкачать

Задача. Решите уравнение √2⋅sin10x + sin2x = cos2xСкачать

ЕГЭ Профиль 12 задание Тренировочный вариант 1 декабрь 2021Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Математика Дано уравнение (1+2(Sinx)^2 -(3^0.5)Sin2x)/(2Sinx-1)=0 А) Решите уравнение.Скачать

Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать

Математика а) Решите уравнение 2Sin2x+2√3 Sinx=2Cosx+√3 б) Укажите корни этого уравненияСкачать