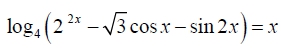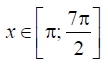Решите уравнение log4 2 2x 3 cos x sin 2x x (5 видео)

Решение №622 Решите уравнение log4(2^2x-√3cosx-sin2x)=x

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Решение:

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.7 / 5. Количество оценок: 19

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Содержание

Калькулятор Уравнений. Решение Уравнений Онлайн
Решение задач по математике онлайн
Калькулятор онлайн. Решение тригонометрических уравнений.
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Уравнение sin(х) = а
Уравнение tg(х) = а
Решение тригонометрических уравнений
Уравнения, сводящиеся к квадратным
Уравнение вида a sin(x) + b cos(x) = c
Уравнения, решаемые разложением левой части на множители
Решите уравнение log4 2 2x 3 cos x sin 2x x
💡 Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Калькулятор Уравнений. Решение Уравнений Онлайн

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:а) Решите уравнение √3/4sinx(cosx-√2)=(√2cosx-cos²x)sin²x. б) Укажите корни этого уравненияСкачать

Калькулятор онлайн.
Решение тригонометрических уравнений.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение

Видео:ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать

Немного теории.

Видео:Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

Тригонометрические уравнения

Видео:Быстрый способ решения уравнения ➜ 9x⁴-6x³-18x²-2x+1=0Скачать

Уравнение cos(х) = а

Из определения косинуса следует, что ( -1 leqslant cos alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.

Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если a

Видео:Решить неравенство cosСкачать

Уравнение sin(х) = а

Из определения синуса следует, что ( -1 leqslant sin alpha leqslant 1 ). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.

Уравнение sin х = а, где ( |a| leqslant 1 ), на отрезке ( left[ -frac; ; frac right] ) имеет только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right] ); если а

Видео:КАК РЕШАТЬ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ? // УРАВНЕНИЕ COSX=AСкачать

Уравнение tg(х) = а

Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.

Уравнение tg x = а для любого a имеет на интервале ( left( -frac; ; frac right) ) только один корень. Если ( |a| geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac right) ); если а

Видео:Простейшие тригонометрические уравнения. y=cosx. 1 часть. 10 класс.Скачать

Решение тригонометрических уравнений

Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.

Видео:Как решать тригонометрическое уравнение cos^2 x =1/2 Уравнение с косинусом в квадрате Решите уравненСкачать

Уравнения, сводящиеся к квадратным

Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0

Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y₁ = -3, y₂ = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; ( x = (-1)^n text(0,5) + pi n = (-1)^n frac + pi n, ; n in mathbb )
Ответ ( x = (-1)^n frac + pi n, ; n in mathbb )

Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0

Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y₁ = 1, y₂ = 1/3

Видео:cos2x=1-cos(p/2-x) тригонометрическое уравнение из ДЕМОварианта ЕГЭСкачать

Уравнение вида a sin(x) + b cos(x) = c

Решить уравнение 2 sin(x) + cos(x) — 2 = 0

Используя формулы ( sin(x) = 2sinfrac cosfrac, ; cos(x) = cos^2 frac -sin^2 frac ) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac + cos^2 frac right) ) получаем

Поделив это уравнение на ( cos^2 frac ) получим равносильное уравнение ( 3 text^2frac — 4 textfrac +1 = 0 )
Обозначая ( textfrac = y ) получаем уравнение 3y 2 — 4y + 1 = 0, откуда y₁=1, y₁= 1/3

В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):

Решить уравнение 4 sin(x) + 3 cos(x) = 5

Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:

Видео:Три способа отбора корней в задании 13 ЕГЭ профиль Скачать

Уравнения, решаемые разложением левой части на множители

Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.

Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0

Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0

Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0

Видео:Хитрый способ решения ★ x^4-2x^3+x=30 ★ Решите уравнениеСкачать

Решите уравнение log4 2 2x 3 cos x sin 2x x

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Решим уравнение

б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

Это синус вначале нужно писать

Нет. Нужно внимательно читать решение задачи, и следить за смыслом, а не бездумно механически действовать по заученным формулам.

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Преобразуем исходное уравнение:

б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:

Ответ : а) б)

если же tgx=1,то там рассматриваются два корня: x=п/4+2пn x=5п/4+2пn

и как раз через эти два корня я нашла корни,принадлежащие промежутку,но почему в ответе под а у вас одно решение?

эти две точки можно объединить, что у нас и сделано

почему при решении было выполнено деление на 3^cos(x), ведь тогда теряется корень 3^cos(x)=0?

такого корня нет, поэтому он не теряется

Извиняюсь, что задаю вопрос не совсем по теме, но когда вообще МОЖНО делить на неизвестное, а когда нельзя? Я не одну статью прочитал на эту тему, но все понять не могу. Одни говорят, что можно, но при этом происходит потеря корней, а другие говорят — что можно и делают это, третьи говорят, что будет потеря корней, но это МОЖНО делать.

Короче говоря. как мне кажется, это самая не разобранная тема. О ней вообще нет инфы в должном обьеме. Пожалуйста, обьсните в кратце, когда МОЖНО, а когда НЕЛЬЗЯ.

p.s. я понял, что МОЖНО, вроде как, когда не происходит изменение ОДЗ, но опять же, а когда оно проиходит?

Думаю, мне не одному этот вопрос требуется.

Подробный ответ ЗДЕСЬ невозможен. Лучше задать его, нажав ссылку «Помощь по заданию».

Если кратко, то правило простое: НЕЛЬЗЯ делить на нуль. На положительные и отрицательные числа делить можно, соблюдая правила.

Число положительно при любом значении , поэтому на него можно делить.