- Определение числа размещений
- Найти число размещений из n элементов по k
- Видеоролик о размещениях
- Размещения
- п.1. Размещения без повторений
- п.2. Размещения с повторениями
- п.3. Примеры
- Число размещений
- Данный онлайн калькулятор позволяет найти число размещений из n элементов по k.
- Алгебра и начала математического анализа. 11 класс
- 🎬 Видео
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Определение числа размещений
Пусть имеется $n$ различных объектов.
Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно
Если вы уже знакомы с сочетаниями, то легко заметите, что чтобы найти размещения, надо взять все возможные сочетания, а потом в каждом еще поменять порядок всеми возможными способами (то есть фактически сделать еще перестановки). Поэтому число размещений еще выражается через число перестановок и сочетаний так:
$$A_n^k= C_n^k cdot k! = C_n^k cdot P_k.$$
Получилась такая изящная формула, объединяющая три других формулы комбинаторики (три концепции: размещений, сочетаний и перестановок).
Пример всех размещений из $n=3$ объектов (различных фруктов) в группы по $m=2$ с учетом порядка — на картинке справа. Согласно формуле, их должно быть ровно $$A_3^2=3cdot (3-2+1)=3cdot 2 =6.$$
Видео:Алгебра 11 класс (Урок№30 - Размещения без повторений.)Скачать

Найти число размещений из n элементов по k
Чтобы вычислить число размещений $A_n^k$ онлайн, используйте калькулятор ниже.
Видео:9 класс, 26 урок, Комбинаторные задачиСкачать

Видеоролик о размещениях
Не все понятно? Посмотрите наш видеообзор для формулы размещений: как использовать Excel для нахождения числа размещений, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Видео:Комбинаторика: размещения, перестановки, сочетанияСкачать

Размещения
п.1. Размещения без повторений
Например:
Для создания 3-значного пароля используются символы из алфавита .
Сколько всего паролей без повторения символов можно составить?
По условию n = 5, k = 3. Рассматриваем размещение 5 символов по 3 позициям без повторений: (mathrm< A_5^3=frac=5cdot 4cdot 3 = 60 >)
Всего 60 паролей.
Результат можно получить непосредственно из правила произведения. Действительно, на первой позиции – 5 вариантов символов, на второй – 4 оставшихся, на третьей – 3 оставшихся. Итого, по правилу произведения: 5 · 4 · 3 = 60 паролей.
п.2. Размещения с повторениями
п.3. Примеры
Пример 1. Исследуйте различие между перестановкой без повторений и размещением без повторений 〈3,2〉-выборок для трёх разноцветных фишек. Изобразите полученные решения.
Рассматриваем фишки:
1) Для перестановок, 〈3,3〉-выборок, получаем:
 | В каждом ряду – отдельная перестановка. Видно, как образуется факториал. Для каждой отдельной фишки – одна перестановка. Для каждой пары фишек – две перестановки: 2 · 1. Когда добавляем третью, получаем: 3 · 2 · 1 Итого: P3 = 3 · 2 · 1 = 6 перестановок. |
2) Для размещений без повторений, 〈3,2〉-выборок, получаем:
 | В каждом ряду – отдельное размещение. В первом столбце слева – 3 варианта по цвету. Во втором столбце остается только 2 варианта. Итого: (mathrm) размещений. |
Пример 2. Исследуйте перестановки без повторений и размещения для 〈4,3〉 выборок и для 〈4,2〉 выборок без повторений из 4 разноцветных фишек.
Изобразите полученные решения.
Рассматриваем фишки:
 В каждом ряду – отдельная перестановка. Итого: P4=4·3·2·1=24 перестановки. |  В каждом ряду – отдельное размещение. Итого: (mathrm) размещения. |  В каждом ряду – отдельное размещение. Итого: (mathrm) размещений. |
Пример 3. Исследуйте различие между перестановкой с повторениями и размещением с повторениями. Сделайте вывод.
Перестановка с повторениями: сколько слов можно получить, переставляя буквы в слове «МАМА»? Запишите все эти слова в лексикографическом порядке.
Размещение с повторениями: сколько 4-буквенных слов можно получить, используя две буквы: «М» и «А»? Запишите все эти слова в лексикографическом порядке.
1) Для перестановки с повторениями получаем: begin mathrm\ mathrm\ mathrm< P_4(2;2)=frac=frac=6 > end Все 6 слов в лексикографическом порядке:
Вывод: вариантов для размещения с повторениями получается больше, т.к. они включают слова с одной, тремя и четырьмя «М» и «А». А в перестановки с повторениями входят только слова с двумя «М» и двумя «А».
Пример 4. В базе данных с номерами телефонов содержатся все 7-значные номера.
1) Сколько в книге номеров, в которых цифры не повторяются?
2) Сколько в книге всего номеров?
3) Сколько в книге номеров, у которых 4 последних цифры одинаковые?
4) Сколько в книге номеров, у которых 4 последних цифры одинаковые, а 3 первых цифры отличаются от 4 последних?
1) Цифр – всего 10:
Видео:02 Комбинаторика ЗадачиСкачать

Число размещений
Пусть имеется n различных объектов. Будем выбирать из них k объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по k, а их число равно:
Пример размещений. Различными размещениями из трех элементов по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2).
Данный онлайн калькулятор позволяет найти число размещений из n элементов по k.
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы, калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать

Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №30. Размещения без повторений.
Комбинаторика, размещения, размещения без повторений.
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под редакцией Жижченко А.Б. Авторская программа «Алгебра и начала анализа 10-11 кл.», авторов
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2010.
Теоретический материал для самостоятельного изучения
Задача: Сколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что в каждой записи нет одинаковых цифр?
Перебором можно убедится, что из данных цифр можно составить 12 двузначных чисел.
В записи двузначного числа, на первом месте может стоять любая из четырех цифр, а на втором месте любая из трех оставшихся. По правилу произведения так же получаем 4*3=12.
При решении задачи, из четырех данных элементов были образованы всевозможные соединения по два элемента в каждом, причем любые два соединения отличались друг от друга либо составом элементов, либо их расположением. Такие соединения называются размещениями.
Определение: Размещениями без повторений из m элементов по n, где 
Задача: Сколькими способами можно обозначить вершины данного треугольника, используя буквы A B C D E F?

Задача: Решите уравнение
Обратим внимание, что
По формуле получаем, что
По условию
Корни: 
🎬 Видео
Комбинаторика. Основные формулы (перестановки, сочетания, размещения) и примеры решения задач.Скачать

Размещения без повторенийСкачать

A.2.3 Комбинаторика: размещения с повторениямиСкачать

Комбинаторика: перестановки, размещения, сочетания. ВероятностьСкачать

Решение комбинаторных задач по теме "Перестановки и размещения с повторениями и без повторений"Скачать

Комбинаторика | перестановки | размещения | сочетанияСкачать

Перестановки в комбинаторике. Размещения без повторений. 9 класс.Скачать
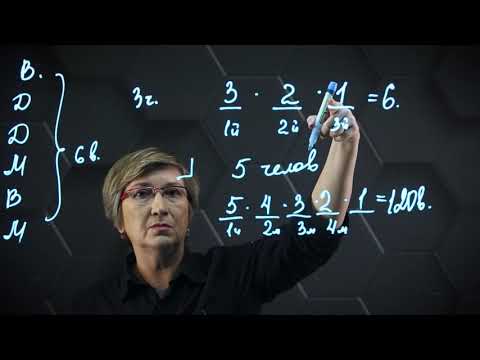
Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

§61 ПерестановкиСкачать

Комбинаторика. Размещение. 10 класс.Скачать

РАЗМЕЩЕНИЯ комбинаторикаСкачать

Учимся дома. 11 класс. Алгебра: Решение комбинаторных задач. Перестановки размещения, сочетанияСкачать

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

A.2.1 Комбинаторика: перестановки и размещенияСкачать










