Решите уравнение ax b при a не равно 0

Уравнение вида ax = b, где x — неизвестное, a и b — числа, называется уравнением с одним неизвестным или линейным уравнением.

Число a называется коэффициентом при неизвестном, а число b — свободным членом.

Если в уравнении ax = b коэффициент не равен нулю (a ≠ 0), то, разделив обе части уравнения на a, получим . Значит, уравнение ax = b, в котором a ≠ 0, имеет единственный корень .

Если в уравнении ax = b коэффициент равен нулю (a = 0), а свободный член не равен нулю (b ≠ 0), то уравнение не имеет корней, так как равенство 0x = b, где b ≠ 0, не является верным ни при каком значении x.

Если в уравнении ax = b и коэффициент, и свободный член равны нулю (a = 0 и b = 0), то уравнение имеет бесконечное множество корней, так как равенство 0x = 0 верно при любом значении x.

Видео:Решение линейного уравнения ax=b. Сколько корней может быть у линейного уравнения. Алгебра 7 класс.Скачать

Решение уравнений с одним неизвестным

Все уравнения с одним неизвестным решаются одинаково с помощью преобразований, которые могут выполняться в любом порядке. Список возможных преобразований, которые могут быть использованы для решения уравнений:

• освобождение от дробных членов;
• раскрытие скобок;
• перенос всех членов, содержащих неизвестное, в одну часть, а известные — в другую (члены с неизвестными, как правило, переносят в левую часть уравнения);
• сделать приведение подобных членов;
• разделить обе части уравнения на коэффициент при неизвестном.

Пример 1. Решить уравнение

Освобождаем уравнение от дробных членов:

20x — 28 — 24 = 9x + 36.

20x — 9x = 36 + 28 + 24.

Выполняем приведение подобных членов:

Делим обе части уравнения на коэффициент при неизвестном (на 11):

Делаем проверку, подставив в данное уравнение вместо x его значение:

Уравнение обратилось в верное равенство, следовательно, корень был найден верно.

Пример 2. Решить уравнение

Это уравнение проще решить, не раскрывая скобок, поэтому делим обе части уравнения на 5:

Выполняем приведение подобных членов:

Обычно все рассуждения при решении уравнения производят устно, а само решение записывается так:

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Уравнения с бесконечным количеством корней

В каком случае уравнение ax = b имеет единственный корень; имеет бесконечно много корней; не имеет корней? Приведите примеры.

Решение

Линейное уравнение ax = b при a ≠ 0 имеет один корень, при a = 0 и b ≠ 0, не имеет корней, при a = 0 и b = 0 имеет бесконечно много корней (любое число является его корнем).

Примеры:
15 x = 30 − один корень;
0 x = 4 − не имеет корней;
0 x = 0 − имеет бесконечно много корней.

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

1. Линейное уравнение. Приведите Примеры линейных уравнений, имеющих один корень, бесконечно много корней и не имеющих корней.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Что ты хочешь узнать?

Видео:2 13 Решение матричного уравнения AXB=CСкачать

Ответ

Проверено экспертом

один корень имеют например

5х=6, или 10х=20, или 5х-4=1 или 9х-7=2 и т.д.

бесконечно много корней имеют например 0х=0; 2(5х+6)=10х+12, или 5х-3х-2х=7-4-3

не имеющие корни например 0х=4 или 2х+5=2х+6 и т.д.

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Видео:Решение матричных уравненийСкачать

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.

Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .

После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня ­­– три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня – 2 , 1 и 5 , то пишем – 2 , 1 , 5 или .

Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых ­– Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.

Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

Видео:Алгебра 7 класс. Линейное уравнение с одной переменной ax=b.Скачать

Неполные квадратные уравнения

О чем эта статья:

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

• если D 0, есть два различных корня.

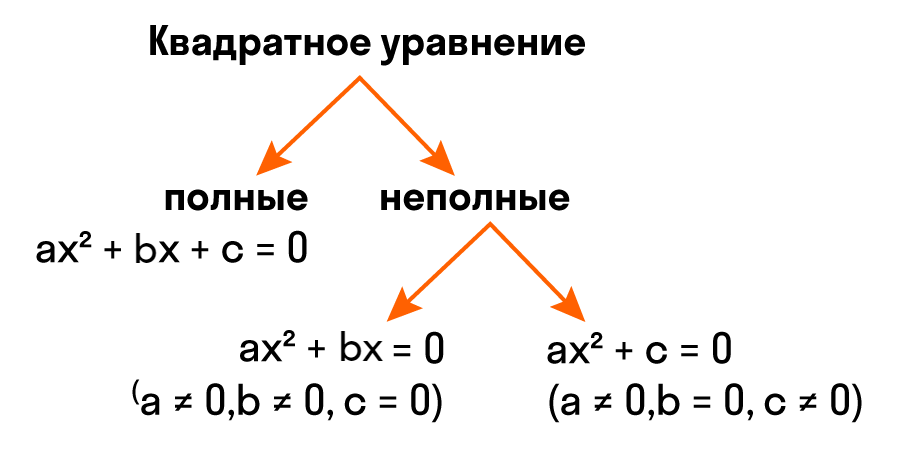
Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов: Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0. Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0. Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать Решение неполных квадратных уравнений Как мы уже знаем, есть три вида неполных квадратных уравнений: ax² = 0, ему отвечают коэффициенты b = 0 и c = 0; ax² + c = 0, при b = 0; ax² + bx = 0, при c = 0. 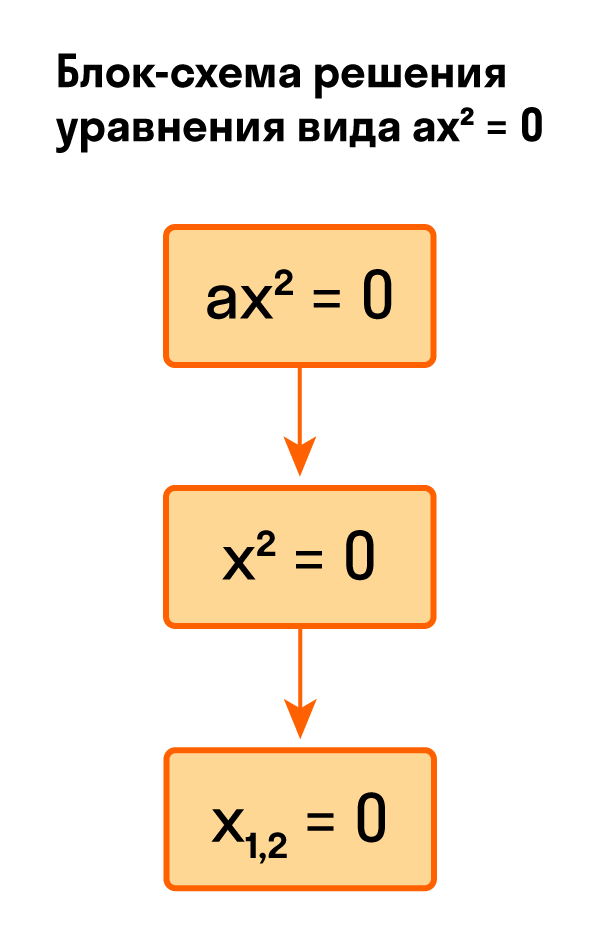Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать Как решить уравнение ax² = 0 Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0. Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль. 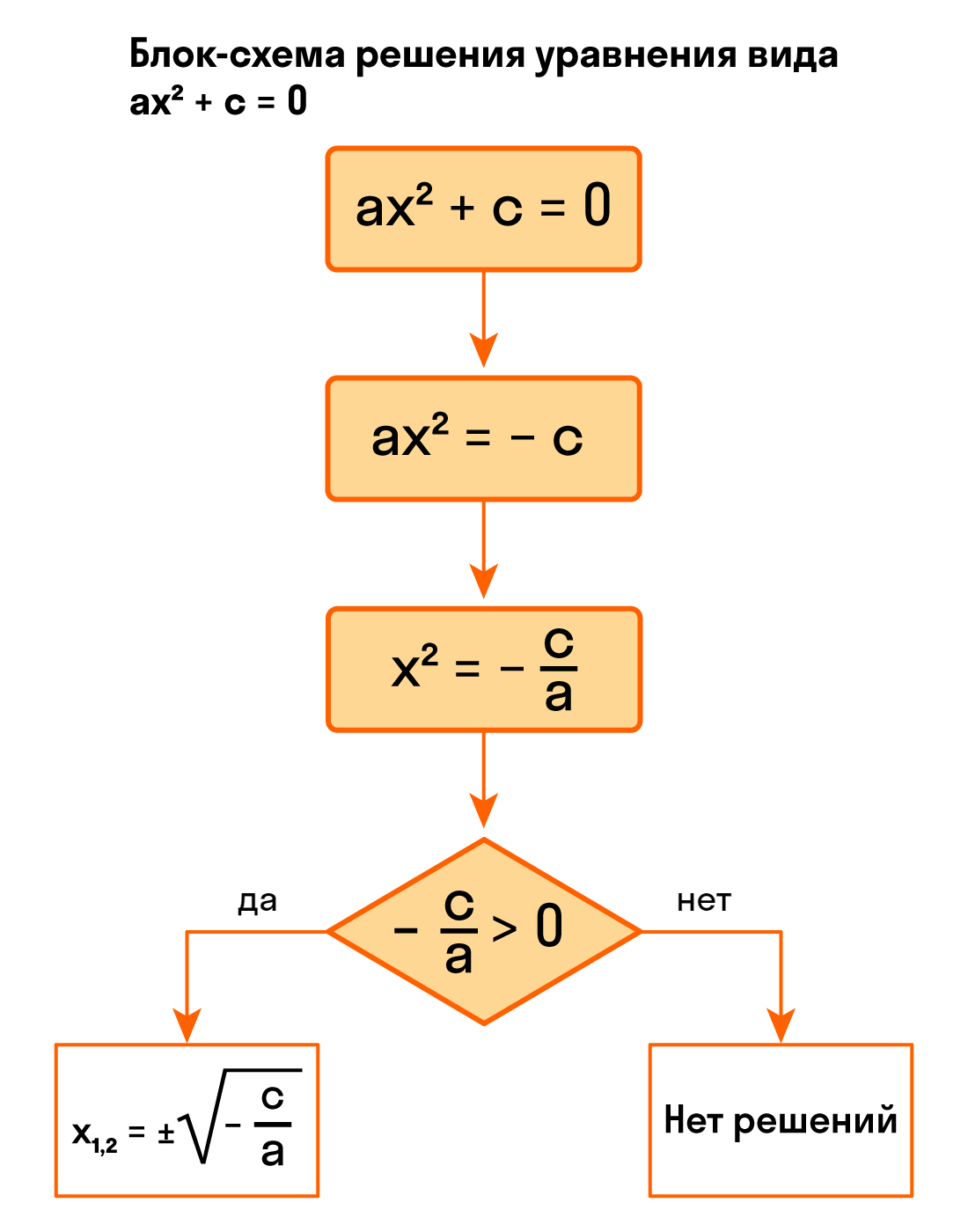По шагам решение выглядит так: Записывайся на дополнительные уроки по математике онлайн, с нашими лучшими преподавателями! Для учеников с 1 по 11 класса! Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать Как решить уравнение ax² + с = 0 Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0: перенесем c в правую часть: ax² = — c, разделим обе части на a: x² = — c/а. Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое: не имеет корней при — c/а 0. Пример 1. Найти решение уравнения 9x² + 4 = 0. Перенесем свободный член в правую часть: Разделим обе части на 9: В правой части осталось число со знаком минус, значит у данного уравнения нет корней. Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0. 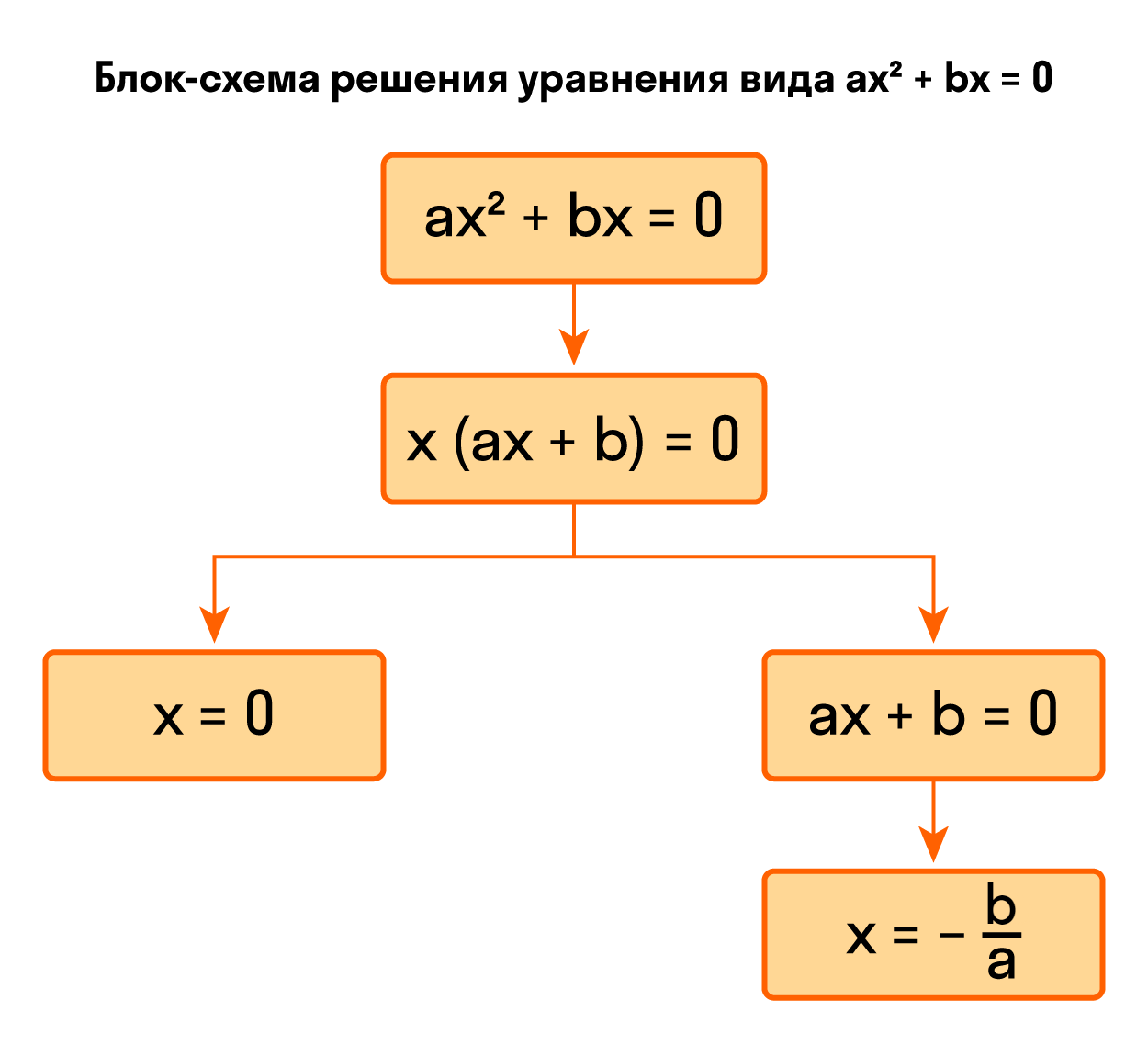Перенесем свободный член в правую часть: Разделим обе части на -1: Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать Как решить уравнение ax² + bx = 0 Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0 Вынести х за скобки Это уравнение равносильно х = 0 и 2x — 32 = 0. Решить линейное уравнение: Значит корни исходного уравнения — 0 и 16. Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Разложить левую часть уравнения на множители и найти корни: Ответ: х = 0 и х = 4. Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке. 🎦 Видео Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать Как решить уравнение #россия #сша #америка #уравненияСкачать Как решить НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ. Часть 2 Уравнение вида ax^2+bx=0Скачать Решение квадратных уравнений. Дискриминант. 8 класс.Скачать Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать Как решать дробно-рациональные уравнения? | МатематикаСкачать Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства