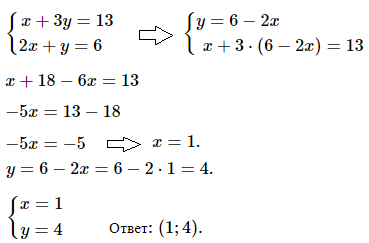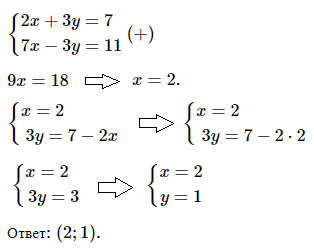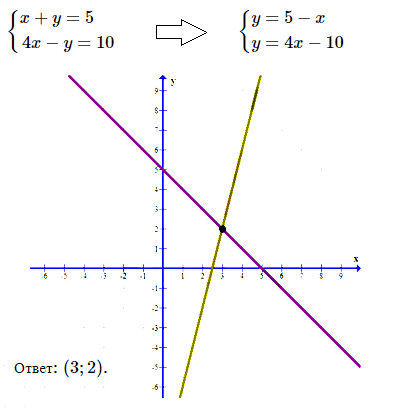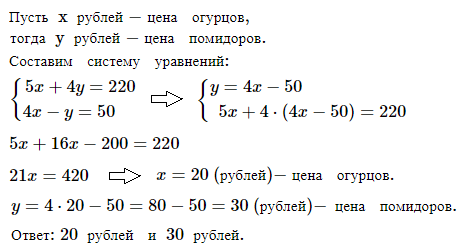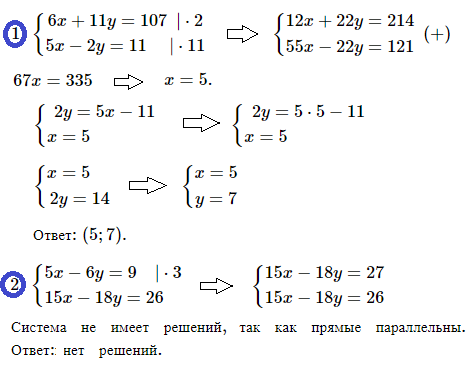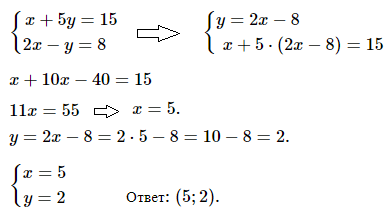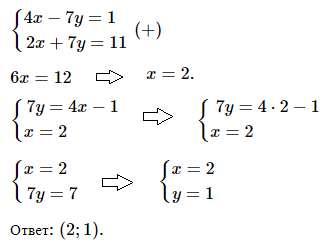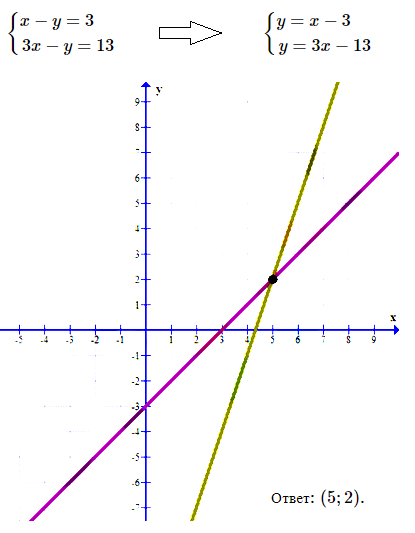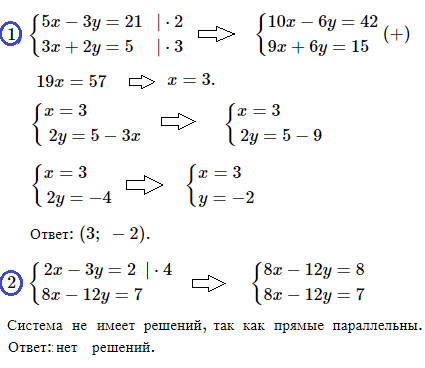Решите методом подстановки систему уравнений x 3y 13 2x y 6 контрольная работа

[left < beginx + 3y = 13 \ 2x + y = 6 \ end right. Longrightarrow left < beginy = 6 — 2x \ x + 3 cdot (6 — 2x) = 13 \ end right. ]

[y = 6 — 2x = 6 — 2 cdot 1 = 4.]

© 2021 Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]

Видео:Решение систем уравнений. Методом подстановки. Выразить YСкачать

Мерзляк 7 класс Контрольная 7 Варианты 1-2

Контрольная работа по алгебре в 7 классе с ответами «Системы линейных уравнений с двумя переменными» (варианты 1, 2) для УМК Мерзляк, Полонский, Якир. Алгебра. Мерзляк 7 класс Контрольная 7 (4 варианта).

Алгебра 7 класс (УМК Мерзляк)
Контрольная работа № 7

Тема: Системы линейных уравнений с двумя переменными

Смотрите также варианты 3 и 4 контрольной работы № 7 тут:

Решения и ОТВЕТЫ на Вариант 1

№ 1. Решите методом подстановки систему уравнений
< х + 3у = 13, < 2х + у = 6.
Решение и ОТВЕТ:

№ 2. Решите методом сложения систему уравнений
< 2х + 3у = 7, < 7x – 3y = 11
Решение и ОТВЕТ:

№ 3. Решите графически систему уравнений
< х + у = 5, < 4х – у = 10.
Решение и ОТВЕТ:

№ 4. За 5 кг огурцов и 4 кг помидоров заплатили 220 р. Сколько стоит килограмм огурцов и сколько стоит килограмм помидоров, если 4 кг огурцов дороже кило грамма помидоров на 50 р.?
Решение и ОТВЕТ:

№ 6. При каком значении а система уравнений
< 4х – aу = 3, < 20х + 10у = 15
имеет бесконечно много решений?
Решение и ОТВЕТ:

Решения и ОТВЕТЫ на Вариант 2

№ 1. Решите методом подстановки систему уравнений
< х + 5у = 15, < 2х – у = 8.
Решение и ОТВЕТ:

№ 2. Решите методом сложения систему уравнений
< 4х – 7у = 1, < 2x + 7y = 11.
Решение и ОТВЕТ:

№ 3. Решите графически систему уравнений
< х – у = 3, < 3х – у = 13.
Решение и ОТВЕТ:

№ 4. Масса 2 слитков олова и 5 слитков свинца равна 33 кг. Какова масса слитка олова и какова масса слитка свинца, если масса 6 слитков олова на 19 кг больше массы слитка свинца?
Решение и ОТВЕТ:

№ 5. Решите систему уравнений:
1) < 5х – 3у = 21, < 3х + 2 у = 5;
2) < 2х – 3у = 2, < 8х – 12у = 7.
Решение и ОТВЕТ:

№ 6. При каком значении а система уравнений
< 3х + ау = 4, < 6х – 2у = 8
имеет бесконечно много решений?
Решение и ОТВЕТ:

Вы смотрели: Алгебра. Мерзляк 7 класс Контрольная 7 Варианты 1-2 из 4-х вариантов. Контрольная работа по алгебре в 7 классе «Системы линейных уравнений с двумя переменными» по УМК Мерзляк, Полонский, Якир. Цитаты из пособия «Алгебра 7 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Смотрите также варианты 3 и 4 контрольной работы № 7 тут:

Видео:Решение систем уравнений методом подстановкиСкачать

Мерзляк 7 класс Контрольная 7 Варианты 1-2: 3 комментария

Можно ответы на 1и 2 вариант

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Предметы

Видео:МЕТОД ПОДСТАНОВКИ 7 класс СИСТЕМА УРАВНЕНИЙСкачать

Новые работы

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Найти контрольную:

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Авторы работ и УМК

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Предметы

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Популярное

Видео:7 класс, 38 урок, Метод подстановкиСкачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:Алгебра 9 класс. Решение систем уравнений через подстановку.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Системы уравнений. Метод подстановкиСкачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Решение систем уравнений. Метод подстановки. 7 классСкачать

Немного теории.

Видео:Решение систем уравнений методом сложенияСкачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:Решение систем уравнений методом подстановки (с решением квадратных уравнений). Алгебра 9 класс.Скачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Видео:Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать

Системы уравнений по-шагам

Видео:Решение систем линейных уравнений методом подстановки (видеоурок) - 7 класс алгебраСкачать

Результат

Примеры систем уравнений

• Метод Гаусса
• Метод Крамера
• Прямой метод
• Система нелинейных уравнений

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

💥 Видео

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Системы уравнений с двумя переменными. Алгебра 9 классСкачать