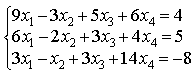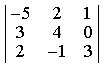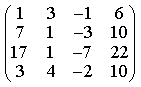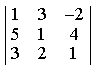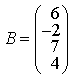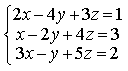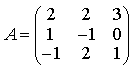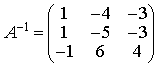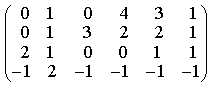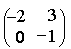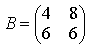- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
- Математика модуль 5 — ответы
- Матричный калькулятор онлайн
- Предупреждение
- Инструкция матричного онлайн калькулятора
- Вычисление суммы, разности, произведения матриц онлайн
- Вычисление обратной матрицы онлайн
- Вычисление определителя матрицы онлайн
- Вычисление ранга матрицы онлайн
- Вычисление псевдообратной матрицы онлайн
- Удаление линейно зависимых строк или столбцов матрицы онлайн
- Скелетное разложение матрицы онлайн
- Решение матричного уравнения или системы линейных уравнений AX=B онлайн
- Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
- LU-разложение или LUP-разложение матрицы онлайн
- Построение ядра (нуль-пространства) матрицы онлайн
- Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
- 🔍 Видео
Видео:2 13 Решение матричного уравнения AXB=CСкачать

Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу 

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: 

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:



Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как 
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Видео:Решение матричных уравненийСкачать

Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде 
Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

Видео:§29 Решение матричного уравненияСкачать

Математика модуль 5 — ответы
Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.
1) Найдите общее решение системы
2) Вычислите определитель
-89
3) Найдите ранг и базисные строки матрицы
2. 1-я строка, 2-я строка
4) Вычислите определитель
0
5) Найдите А × В, где 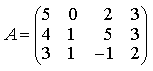
6) Решите систему уравнений методом Крамера
7) Найдите обратную матрицу для матрицы
8) Найдите ранг матрицы
4
9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что
система имеет единственное решений
11) Метод Гаусса решения системы линейных уравнений предполагает использование
последовательного исключения неизвестных
12) Система линейных уравнений называется совместной, если
она имеет хотя бы одно решение
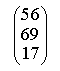
13) Решите матричное уравнение AX + AXA = B, где 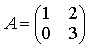
Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Матричный калькулятор онлайн
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:§28 Матричные уравненияСкачать

Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы 
Кнопка 



При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы 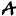
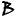
Видео:Матричное уравнениеСкачать

Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Видео:Лекция 8. Решение матричных уравненийСкачать

Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «обратное «.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Видео:Решить матричное уравнениеСкачать

Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Видео:Матричные уравненияСкачать

Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Видео:Матричный метод решения систем уравненийСкачать

Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу
или
с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Видео:Обратная матрицаСкачать

Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц
и
.
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы 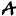
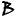
Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
Видео:Решение матричного уравнения X(2 3 2; 1 2 −3; 3 4 1) = (1 0 3; 4 1 4; 2 −1 3) Высшая математика.Скачать

LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Видео:Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу
или
с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».
🔍 Видео
Решение системы уравнений методом ГауссаСкачать

9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

Решение системы уравнений методом обратной матрицы.Скачать