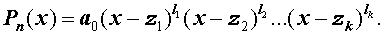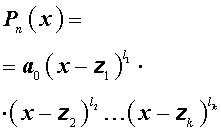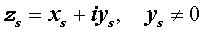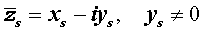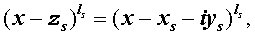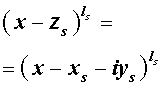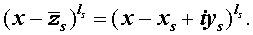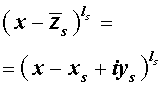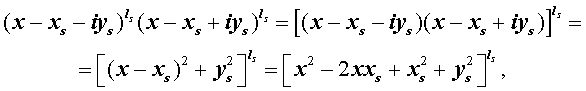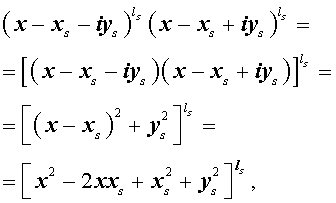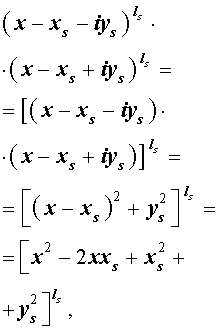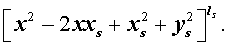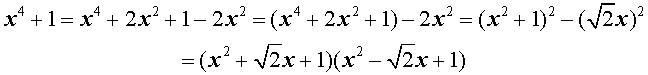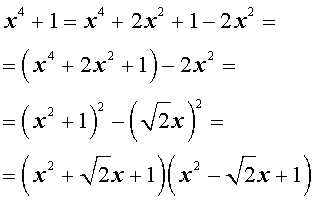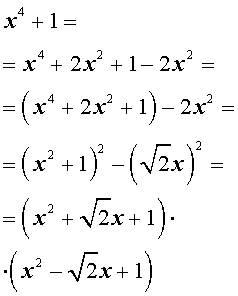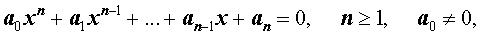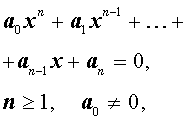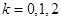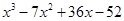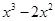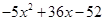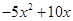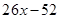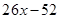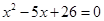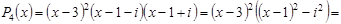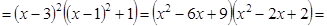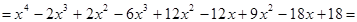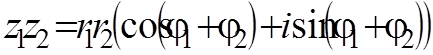Решить уравнения на множестве комплексных чисел и разложить многочлен на множители

Алгебраические уравнения

Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области

Разложение на множители многочленов с действительными коэффициентами

Теорема (формулы) Виета

Алгебраические уравнения

Пусть n – произвольное натуральное число. Рассмотрим многочлен n – ой степени от переменной x

Pn (x) = = a0 x n + a1 x n –1 + + … + an –1 x + an ,

(1)

a0 , a1 , … , an –1 , an

(2)

Заметим, что в этом случае коэффициент a₀ отличен от нуля, и введем следующее определение.

Определение 1 . Алгебраическим уравнением степени n с неизвестным x называют уравнение вида

Pn (x) = 0 .

(3)

Определение 2 . Корнем уравнения (3) называют вещественное или комплексное число α , для которого

Определение 3 . Число α называют корнем кратности k уравнения (3), если справедливо равенство

.

Разложение многочленов на множители в комплексной области

Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет n корней, при условии, что каждый корень считается столько раз, какова его кратность.

– полный набор корней уравнения (3), а

– их кратности, то, во-первых,

а, во-вторых, справедливо равенство

Замечание . Линейными множителями называют многочлены первой степени

входящие в формулу (4), а саму формулу (4) называют формулой разложения многочленов на линейные множители в комплексной области .

Разложение на множители многочленов с действительными коэффициентами

Рассмотрим теперь многочлены степени , все коэффициенты которых являются вещественными числами.

Тогда справедливо следующее

Утверждение . Если комплексное число

является корнем кратности l_s многочлена с вещественными коэффициентами, то и комплексно сопряженное число

является корнем этого многочлена, причем тоже кратности l_s .

Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень z_s и имеющая вид

входит в паре со степенью бинома, содержащей комплексно сопряженный корень 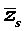и имеющей вид

то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:

Следствие . Каждый многочлен ненулевой степени, коэффициенты которого являются вещественными числами, разлагается на множители, являющиеся многочленами с вещественными коэффициентами первой или второй степени.

Пример . Разложить на множители многочлен четвертой степени

Теорема (формулы) Виета

Снова рассмотрим уравнение n – ой степени от переменной x

и, немного изменив предыдущие обозначения, предположим, что

z1 , z2 , … , zn –1 , zn

(8)

— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.

Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения n – ой степени :

Примеры решения алгебраических уравнений на множестве комплексных чисел (Приведите примеры решения алгебраических уравнений на множестве комплексных чисел)

1. Алгебраические уравнения первой степени:

, – единственный простой корень.

.

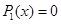
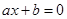
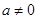
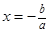
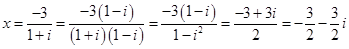
Ответ: .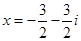

2. Квадратные уравнения:

, – всегда имеет два корня (различных или равных).

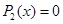
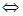
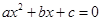
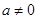
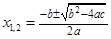
1) .

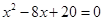
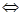
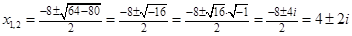
Ответ: .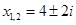

2) .

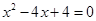
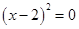
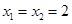
Ответ: .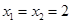

3) , .

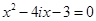
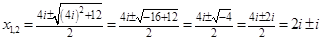
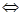
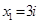
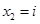
Ответ: , .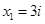

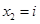
3. Двучленные уравнения степени :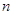

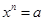
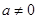
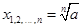
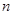
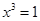
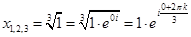
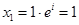
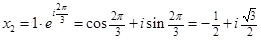
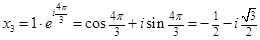
, – всегда имеет различных корней.

,

;

;

.

Ответ: , .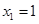

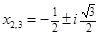
4. Решить кубическое уравнение .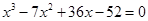

Уравнение третьей степени 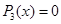имеет три корня (действительные или комплексные), при этом нужно считать каждый корень столько раз, какова его кратность. Так как все коэффициенты данного уравнения являются действительными числами, то комплексные корни уравнения, если они есть, будут парными комплексно сопряженными.

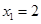
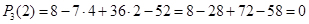
Подбором находим первый корень уравнения , так как .

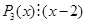
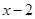
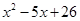
По следствию из теоремы Безу . Вычисляем это деление «в столбик»:

_

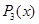
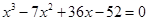
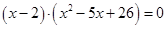
Представляя теперь многочлен в виде произведения линейно и квадратного множителя, получим:

.

Другие корни находим как корни квадратного уравнения:

.

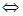
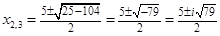
Ответ: , .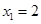

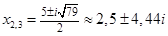
5. Составить алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x1 = 3 и x2 = 1 + i являются его корнями, причем x1 является двукратным корнем, а x2 — простым.

Число 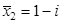тоже является корнем уравнения, т.к. коэффициенты уравнения должны быть действительными.

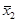
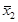
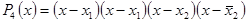
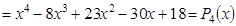
Всего искомое уравнение имеет 4 корня: x1, x1, x2, . Поэтому его степень равна 4. Составляем многочлен 4-й степени с нулями x1, x1, x2, по формуле (6):

Þ

.

Искомое уравнение имеет вид P4(x) = 0.

Ответ: .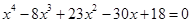

Вопросы для самопроверки

1. Сформулируйте определение комплексного числа

2. Что называется комплексным числом?

3. Какое название или смысл имеет формула?

4. Поясните смысл обозначений в этой формуле:

5. ⌂ .

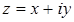
6. Что такое мнимая единица?

7. Что такое действительная часть комплексного числа z?

8. Что такое мнимая часть комплексного числа z?

9. Что такое комплексно сопряженное число?

10. Что такое противоположное число?

11. Что такое комплексный ноль?

12. Что такое чисто мнимое число?

13. Сформулируйте смысл комплексного равенства.

14. В чём состоит геометрическое изображение комплексных чисел?

15. Что такое модуль и аргумент комплексного числа?

16. Что называется модулем комплексного числа?

17. Что такое аргумент комплексного числа?

18. Какое название или смысл имеет формула?

19. Поясните смысл обозначений в этой формуле:

20. ⌂ .

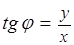
21. Что такое алгебраическая и тригонометрическая формы комплексного числа?

22. Какое название или смысл имеет формула?

23. Поясните смысл обозначений в этой формуле:

24. ⌂ .

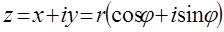
25. Что называется алгебраической формой комплексного числа?

26. Что называется тригонометрической формой комплексного числа?

27. Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.

28. Какое название или смысл имеет формула?

29. Поясните смысл обозначений в этой формуле:

31. Какое название или смысл имеет формула?

32. Поясните смысл обозначений в этой формуле:

33. ⌂ .

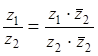
34. Какое название или смысл имеет формула?

35. Поясните смысл обозначений в этой формуле:

36. ⌂ .

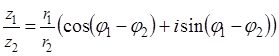
37. Что такое формула Муавра?

38. Какое название или смысл имеет формула?

39. Поясните смысл обозначений в этой формуле:

40. ⌂ .

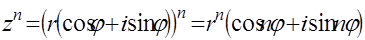
41. Что называется корнем степени n из комплексного числа?

42. Какое название или смысл имеет формула?

43. Поясните смысл обозначений в этой формуле:

44. ⌂ .

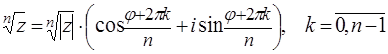
45. Что называется показательной формой комплексного числа?

46. Какое название или смысл имеет формула?

47. Поясните смысл обозначений в этой формуле:

48. ⌂ .

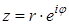
49. Что такое формулы Эйлера?

50. Какое название или смысл имеет формула?

51. Поясните смысл обозначений в этой формуле:

52. ⌂ .

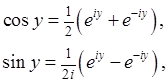
53. Что называется целой функцией?

54. Что называется алгебраическим многочленом?

55. Что называется полиномом?

56. Что такое степень многочлена?

57. Что такое коэффициенты многочлена?

58. Что называется алгебраическим уравнением n-й степени?

59. Что называется нулем функции?

60. Что называется корнем уравнения?

61. Перечислите основные свойства многочленов.

62. Сформулируйте свойство о тождественном равенстве многочленов.

63. Сформулируйте свойство о делении многочлена на разность (x – х0).

64. Сформулируйте теорему теорема Безу.

65. Какое название или смысл имеет формула?

66. Поясните смысл обозначений в этой формуле:

67. ⌂ .

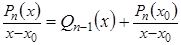
68. Сформулируйте свойство о существовании нуля многочлена.

69. Сформулируйте теорему теорема алгебры основная.

70. Какое название или смысл имеет формула?

71. Поясните смысл обозначений в этой формуле:

72. ⌂ .

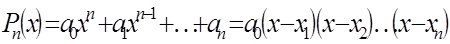
73. Что называется k-кратным нулем многочлена?

74. Что называется простым нулем многочлена?

75. Сформулируйте свойство о количестве корней алгебраического уравнения.

76. Сформулируйте свойство о комплексных корнях алгебраического уравнения

77. с действительными коэффициентами.

78. Сформулируйте свойство о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители.

79. Приведите примеры решения алгебраических уравнений на множестве комплексных чисел

k-кратным нулем многочлена называется. (стр. 18)

алгебраическим многочленом называется. (стр. 14)

алгебраическим уравнением n-й степени называется. (стр. 14)

алгебраической формой комплексного числа называется. (стр. 5)

аргумент комплексного числа это. (стр. 4)

действительная часть комплексного числа z это. (стр. 2)

комплексно сопряженное число это. (стр. 2)

комплексный ноль это. (стр. 2)

комплексным числом называется. (стр. 2)

корнем степени n из комплексного числа называется. (стр. 10)

корнем уравнения называется. (стр. 14)

коэффициенты многочлена это. (стр. 14)

мнимая единица это. (стр. 2)

мнимая часть комплексного числа z это. (стр. 2)

модулем комплексного числа называется. (стр. 4)

нулем функции называется. (стр. 14)

показательной формой комплексного числа называется. (стр. 11)

полиномом называется. (стр. 14)

простым нулем многочлена называется. (стр. 18)

противоположное число это. (стр. 2)

степень многочлена это. (стр. 14)

тригонометрической формой комплексного числа называется. (стр. 5)

Комплексные числа и многочлены

Вы будете перенаправлены на Автор24

После долгих сомнений, которые длились более столетия, известные математики пришли к единому заключению, что необходимо ввести некоторый новый вид чисел, который назвали комплексными числами.

Выражение вида $z=a+bi$, где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=sqrt $ или $i^ =-1$.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Записать комплексно-сопряженные числа для заданных комплексных чисел:

$1) z_ =12+3i; 2) z_ =5; 3) z_ =-2i.$

Для комплексного числа $z=a+bi$ комплексно-сопряженным будет являться число $overline=a-bi$.

Для числа $z_ =12+3i$ получим $overline <z_>=12-3i$.

Для числа $z_ =5$ получим $overline <z_>=5$.

Для числа $z_ =-2i$ получим $overline <z_>=2i$.

Некоторые комплексные числа $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ называются равными, если выполняются следующие равенства $a_ =a_ ,b_ =b_ $. Обозначение: $z_ =z_ $.

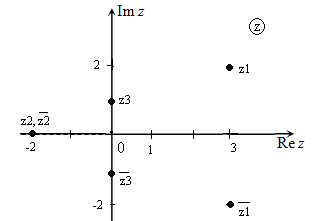
Любое комплексное число можно изобразить на плоскости, которую принято называть комплексной плоскостью. Комплексная плоскость аналогична прямоугольной декартовой системе координат, исключение составляют только названия осей:

• действительная ось (соответствует оси абсцисс);
• мнимая ось (соответствует оси ординат) (рис.1).

Выделяют три формы представления (записи) комплексных чисел:

• алгебраическая;
• тригонометрическая;
• показательная.

Алгебраическая форма записи

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

$a$ — вещественная (действительная) часть, обозначение $Rez=a$;

$b$ — мнимая часть, обозначение $Imz=b$.

Тригонометрическая форма записи

Запись комплексного числа $z$ в виде $z=rcdot (cos varphi +isin varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый формулой $r=|z|=|a+bi|=sqrt <a^+b^ > $, а $varphi $ — аргумент комплексного числа $z$, определяемый по формуле $varphi =arctgfrac $.

Показательная форма записи

Запись комплексного числа $z$ в виде $z=rcdot e^ $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=sqrt <a^+b^ > $, $varphi $ — аргумент комплексного числа $z$, определяемый по формуле $varphi =arctgfrac $.

Над комплексными числами можно выполнять следующие действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Операции над комплексными числами

Сумма

Суммой двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое определяется равенством $z_ +z_ =(a_ +b_ i)+(a_ +b_ i)=(a_ +a_ )+(b_ +b_ )cdot i. $

Разность

Разностью двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое определяется равенством $z_ -z_ =(a_ +b_ i)-(a_ +b_ i)=(a_ -a_ )+(b_ -b_ )cdot i.$

Произведение

Произведением двух заданных комплексных чисел $z_ =a_ +b_ i$ и $z_ =a_ +b_ i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^ =-1$.

Произведением двух заданных комплексных чисел $z_ =r_ cdot (cos varphi _ +isin varphi _ )$ и $z_ =r_ cdot (cos varphi _ +isin varphi _ )$ является комплексное число, которое определяется равенством $z_ cdot z_ =r_ cdot r_ cdot [cos (varphi _ +varphi _ )+isin (varphi _ +varphi _ )].$

Частное

Частным двух заданных комплексных чисел $z_ =r_ cdot (cos varphi _ +isin varphi _ )$ и $z_ =r_ cdot (cos varphi _ +isin varphi _ )$ является комплексное число, которое определяется равенством $z_ cdot z_ =frac <r_> <r_> cdot [cos (varphi _ -varphi _ )+isin (varphi _ -varphi _ )].$

Степень порядка

Степенью порядка $n$ комплексного числа $z=rcdot (cos varphi +isin varphi )$ является комплексное число, которое определяется равенством $z^ =r^ cdot (cos nvarphi +isin nvarphi _ ). $

Данная формула называется формулой Муавра.

Корень

Корнем $n$-й степени комплексного числа $z=rcdot (cos varphi +isin varphi )$ является комплексное число, которое определяется равенством $sqrt[] =sqrt[] cdot (cos frac +isin frac ),, , , k=0..n-1.$

Готовые работы на аналогичную тему

Выполнить действия: 1) $z_ +z_ $; 2) $z_ -z_ $; 3) $z_ cdot z_ $ для комплексных чисел $z_ =1+3i$ и $z_ =1-2i$.

$3) z_ cdot z_ =(1+3i)cdot (1-2i)=1cdot 1+1cdot 3i-1cdot 2i-3cdot 2cdot i^ =1+3i-2i+6=7+i $

Выполнить умножение и деление заданных комплексных чисел:

$z_ =sqrt cdot (cos pi +icdot sin pi )$ и $z_ =sqrt cdot (cos pi +icdot sin pi )$.

1) $ <z_cdot z_ =left(sqrt cdot (cos pi +icdot sin pi )right)cdot left(sqrt cdot (cos pi +icdot sin pi )right)=sqrt cdot sqrt cdot [cos (pi +pi )+icdot sin (pi +pi )]=> \ $

2) $ <z_=left(sqrt cdot (cos pi +icdot sin pi )right)div left(sqrt cdot (cos pi +icdot sin pi )right)=frac <sqrt> <sqrt> cdot [cos (pi -pi )+icdot sin (pi -pi )]=> \ $

Многочлен

Многочленом $n$-ой степени называется функция

где коэффициенты $a_ ,a_ ,a_ . a_ ,a_ $ — постоянные комплексные числа, $a_ ne 0$, $zin Z$ — комплексная переменная. Число $z_ $, при котором заданный многочлен принимает нулевое значение ($P_ (z_ )=0$), называется корнем этого многочлена.

Любой многочлен степени $n$ может быть представлен как разложение многочлена на $n$ линейных сомножителей вида $z-a$ и множитель, который равен коэффициенту при $z^ $:

$$P_ (z)=A_ cdot (z-a_ )cdot (z-a_ )cdot . cdot (z-a_ ), $$

где $a_ ,a_ . a_ $ — корни многочлена.

Если в разложении многочлена степени $n$ на линейные множители

$P_ (x)=A_ cdot (z-a_ )cdot (z-a_ )cdot . cdot (z-a_ ), (*) $

некоторые линейные сомножители оказываются одинаковыми, то данные множители можно объединить, тогда разложение заданного многочлена на сомножители будет иметь следующий вид:

В формуле (*) корни многочлена $a_ ,a_ . a_ $ могут быть не только вещественными, но и комплексными числами.

Для многочленов определены следующие операции: вычитание, сложение, умножение. Операция деления многочленов определена не для любых двух многочленов, однако, как и для целых чисел, имеется возможность выполнить деление с остатком.

🌟 Видео