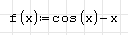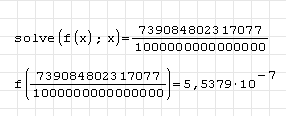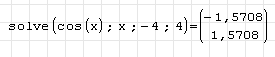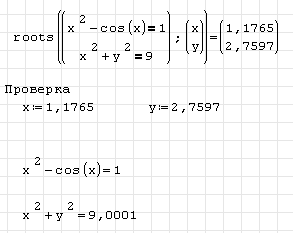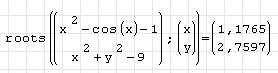Модуль 2
Решение иженерных задач средствами
Компьютерной математики
Лабораторная работа № 2
Нахождение корней нелинейных уравнений. Решение систем нелинейных уравнений
Цель: изучить основные возможности приложения Smath Studio для решения нелинейных уравнений и систем.
Вопросы для самоконтроля
1. Что является корнем уравнения?
2. Правило записи функции для использования команды solve.
3. В чем разница между численным и аналитическим нахождением корней уравнения?
4. Чем отличаются команды solve(2) и solve(4).
5. Для чего используется функция polyroots?
6. Правило записи вектора коэффициентов для polyroots.
7. Что является решение системы уравнений?
8. Правило записи уравнений для использования команды roots.
9. В чем разница между численным и аналитическим решениями системы уравнений?
10. Чем отличаются команды roots (2) и roots (3).
Индивидуальные задания 1
Найти корень уравнения численно и, если это возможно, аналитически. Результаты сравнить. Выполнить проверку.
| № варианта | Уравнение | № варианта | Уравнение |
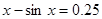 |  | ||
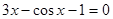 |  | ||
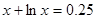 | 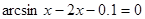 | ||
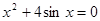 | 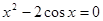 | ||
 | 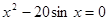 | ||
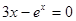 | 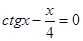 | ||
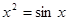 | 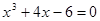 | ||
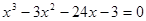 |  | ||
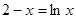 | 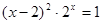 | ||
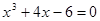 | 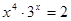 | ||
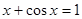 | 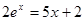 | ||
 | 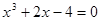 | ||
 |
Индивидуальные задания 2
Найти численно корни полинома. Выполнить проверку.
| Вариант | Полином | Вариант | Полином |
| x 2 -12x-4=0 | x 3 -3x 2 -4x+1=0 | ||
| x 3 -24x+11=0 | x 3 -34x 2 +4x+1=0 | ||
| x 3 +2x-7=0 | x 3 -27x-17=0 | ||
| x 3 -21x+7=0 | x 4 -2x 3 +2x 2 -2x+1=0 | ||
| x 3 -5x+1=0 | x 4 -3x 3 +3x 2 -3x+2=0 | ||
| x 3 -12x+5=0 | x 4 -3x 3 +5x 2 -3x+8=0 | ||
| x 3 +3x 2 -4x-1=0 | x 4 -4x 3 +8x 2 -4x+16=0 | ||
| x 3 -9x 2 +20x-11=0 | x 4 -4x 3 +4x 2 -4x+3=0 | ||
| x 3 -12x+5=0 | x 4 -4x 3 +12x 2 -4x+27=0 | ||
| x 3 +6x 2 +6x-7=0 | x 4 -6x 3 +18x 2 -6x+81=0 | ||
| x 3 -3x 2 -x+2=0 | x 4 -5x 3 +10x 2 -5x+24=0 | ||
| x 3 -10x 2 +4x+9=0 | x 4 -5x 3 +15x 2 -5x+54=0 | ||
| x 4 +x-1=0 |
Индивидуальные задания 3
Найти численное решение системы. Выполнить проверку.
| № варианта | Система уравнений | Начальная точка |
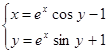 | (-0,9;1,4) | |
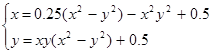 | (1;1) | |
 | (1;1) | |
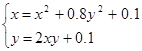 | (0;0) | |
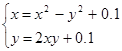 | (0;0) | |
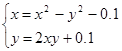 | (0;0) | |
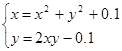 | (0;0) | |
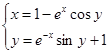 | (0,9;1,4) | |
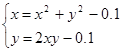 | (0;0) |
| № варианта | Система уравнений | Начальная точка |
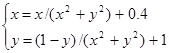 | (1;1) | |
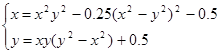 | (-0,5;0,5) | |
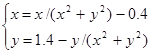 | (-1;1) | |
 | (0;0) | |
 | (0;0) | |
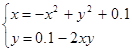 | (0;0) | |
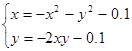 | (0;0) | |
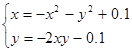 | (0;0) | |
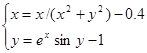 | (-1;1) | |
 | (-0,9;-1,4) | |
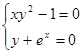 | (0,5;-1,5) | |
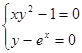 | (0,5;1,5) | |
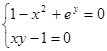 | (2;2) | |
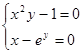 | (1,5;0,5) | |
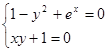 | (-2;2) | |
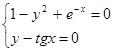 | (0;1) |
Пример выполнения задания 1
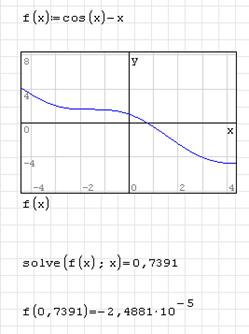
Найти корень уравнения 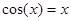
Методические рекомендации
1. Запишите функцию (предварительно приведя уравнение к виду f(x)=0): 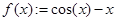
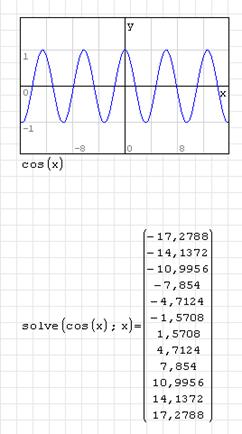
2. Постройте график функции. График пересекает ось абсцисс в одной точке, значит, уравнение имеет один корень.
3. Запишите стандартную команду:
Справа от знака равенства увидим результат: 0,7391.
2 Выполните проверку, найдя значение функции в полученной точке:
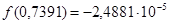
Если бы решение было точным, то при проверке получили бы 0. Значение 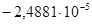
Конечный вид документа SMathStudio:
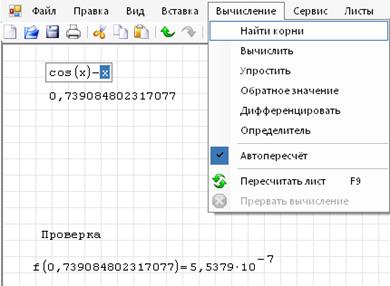
1. Запишите функцию в виде: 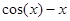
2 Выделите курсором переменную х.
3. В меню выбрать Вычисление ® Найти корни.
4. Выполните проверку.
1. Конечный вид документа SMathStudio:
1. Запишите функцию: 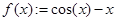
2. Для получения аналитического решения запишите стандартную команду:
solve(f(x) ; x), после которой на ПИ «Арифметика» выберите →.
3. Выполните проверку, найдя значение функции в полученной точке.
Конечный вид документа SMathStudio:
Если бы решение было точным, то при проверке получили бы 0. Значение 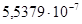
Если уравнение имеет несколько корней (как, например, уравнение 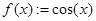
Корни выдаются в диапазоне «по умолчанию» [-20; 20]. Изменить диапазон можно в меню Сервис – Опции – Вычисление.
Можно использовать второй вариант этой процедуры для выбора решения на заданном промежутке. Для этого при наборе solve во всплывающей подсказке выбираем solve(4) и в шаблон вписываем:
Solve( ; ; левая граница интервала; правая граница интервала). Получим:
Если функция f(x) в уравнении f(x)=0 представляет собой полином степени n, то процедура solve может выдать только один корень. Чтобы получить все корни полинома (их количество совпадает со степенью полинома), стоит использовать встроенную функцию polyroots(v). Например, найдем численно корни полинома x 3 +2x-1=0.
1) задаем функцию (левую часть уравнения f(x)=0).
2) задаем вектор коэффициентов (кнопка на ПИ «Матрица»), в появившемся диалоговом окне указываем количество строк (равно степени полинома +1) и столбцов (количество уравнений).
3) записываем функцию polyroots(v)=.
4) делаем проверку, подставив найденные значения в функцию.
Конечный вид документа Smath Studio:
Пример выполнения задания 2
Решить систему уравнений 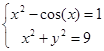
Методические рекомендации
1. Записываем функцию roots( ; ).
2. Для получения численного решения ставим знак «=». Получим результат с заданным количеством знаков после запятой.
3. Выполняем проверку, подставив полученные значения в исходную систему уравнений. В данном примере 1-ое уравнение решено точно, 2-ое – с точностью до 3-го знака.
4. Вид документа SMathStudio:
Можно каждое уравнение системы привести к виду f(x)=0. Тогда запись решения будет выглядеть следующим образом:
Если нужно получить одно из нескольких возможных решений, можно задать начальное приближение (координаты ближайшей известной к ответу точки) для переменных следующим образом:
- Решить уравнение в smath studio
- Обзор доступных библиотек для численного решения жёстких ОДУ
- 1. Intel ODE Solvers Library
- 2. GNU Scientific Library (GSL)
- 3. Matlab C++ Math Library 2.1 (Win32)
- 4. Octave C++ Math Library (Win32)
- 5. DotNumerics
- Обновление (12.07.2014).
- 6. boost::odeint
- 7. SADEL (Sets of Algebraic and Differential Equations solvers Library)
- 8. Решатель Лимонова А. Г.
- 📹 Видео
Видео:SMath Studio - Урок 3 - Решение систем уравненийСкачать

Решить уравнение в smath studio
4.1 Вставка математики
Вы можете поместить математические уравнения и выражения куда угодно, где Вы хотите, на рабочем листе SMath Studio. Все, что Вы должны сделать, щелкнуть в рабочем листе и начать печатать.
1. Щелкните где угодно в рабочем листе. Вы видите небольшое перекрестие. Все, что Вы печатаете, появляется в перекрестии.
2. Напечатайте числа, символы, и математические операторы, или вставьте их, щелкая кнопками на математических панелях инструментов SMath Studio, чтобы создать математическую область .
Вы заметите, что в отличие от текстового процессора, SMath Studio по умолчанию понимает что-либо, что Вы печатаете в курсоре перекрестия как математику. Если Вы хотите создать текстовую область вместо этого, следуйте за инструкциями, описанными в Главе 5, “Работа с текстом”.
Вы можете также напечатать математические выражения в любой математической метке-заполнителе, которая появляется, когда Вы вводите определенные операторы. См. главу 9, «Операторы», для более подробного описания математических операторах SMath Studio и метках-заполнителях, которые появляются, когда Вы их вставляете.
Остальная часть этой главы представляет элементы математических выражений в SMath Studio и описывает методы, которые Вы используете, чтобы построить и отредактировать их. См. главы в разделе Вычислительные Особенности этого руководства пользователя для более полного описания числового и символического вычислений в SMath Studio.
Числа и Комплексные числа
Этот раздел описывает различные типы чисел, которые использует SMath Studio, и их ввод в математические выражения. Одно число в SMath Studio называют скаляром . Для информации о вводе группы чисел в массивы см. “Векторы и Матрицы”.
В математических областях SMath Studio интерпретирует что-либо начинающееся с одной из цифр 0-9 как число. Цифра может сопровождаться:
цифрами после десятичной точки;
символом i для мнимого числа.
Мнимые и комплексные числа
Чтобы задать комплексное число, поставьте за ним символ i, например 1i. SMath Studio задает комплексное число в виде a+b i, где a и b – обычные числа.
Экспоненциальное представление чисел
Чтобы ввести очень большие или очень небольшие числа в экспоненциальное представление чисел, только умножьте число на 10 в нужной степеи. Например, чтобы представить число , наберите 3*10^8.
Векторы и матрицы
Столбец чисел – это вектор , а прямоугольное множество чисел называют матрицей . Общий термин для вектора или матрицы – массив .
Есть много способов создать массив в SMath Studio. Один из самых простых, заполняя массив из пустых меток-заполнителей, как показано в этом разделе. Этот метод полезен для массивов, которые не являются слишком большими. См. Главу 11, “Векторы, Матрицы, и Массивы Данных,” для дополнительных методов для того, чтобы создать массивы произвольного размера.
Создание вектора или матрицы
Для создания вектора или матрицы в SMath Studio необходимо сделать следующие действия:
1. Выберите Матрица из меню Вставка или нажмите Матрицы . Диалоговое окно, показанное справа, появляется.
2. Введите число строк и число столбцов в соответствующих полях. В этом примере будут две строки и три столбца. После этого нажмите «ОК». SMath Studio вставляет матрицу с пустыми метками-заполнителями.
3. Заполните метки-заполнители для формирования матрицы. Можно использовать клавиши горизонтального перемещения курсора для перехода от одной метки-заполнителя к другой
Вы можете использовать эту матрицу в уравнениях, так же, как если бы она была бы числом.
Вы можете менять число строк и столбцов в уже имеющейся матрице. См. раздел «Изменение размерности вектора или матрицы»
Всюду в этом Руководстве пользователя термин «вектор» относится к вектору-столбцу. Вектор-столбец — просто матрица с одним столбцом. Вы можете также создать вектор-строку, создавая матрицу с одной строкой и несколькими столбцами.
Хотя в большинстве случаев математические выражения или переменные, с которыми Вы работаете в SMath Studio, являются числами или массивами, Вы можете также работать со строками (также назваемые строкой символов или строкой переменных). Ряды могут включать любую цифру, которую Вы можете напечатать в клавиатуре, включая символы, числа, пунктуацию, и пробел. Строки отличаются от имен переменной или чисел, потому что SMath Studio всегда показывает их между двойными кавычками. Вы можете назначить строку на имя переменной, использовать строку в качестве элемента вектора или матрицы, или использовать строку в качестве аргумента функции.
Для создания строки:
1. Нажмите на пустую математическую метку-заполнитель в математическом выражении, обычно на правой стороне определяемой переменной.
2. Напечатайте символ двойной кавычки («). SMath Studio показывает пару кавычек и линию вставки между ними.
3. Напечатайте любую комбинацию символов, чисел, пунктуации, или пробелов. Щелкните вне выражения, когда Вы закончите.
У клавиши двойной кавычки («) есть несколько предназначений в SMath Studio, в зависимости от точного местоположения курсора в Вашем рабочем листе. Когда Вы хотите создать строку, у Вас должен всегда быть курсор в отобранной метке-заполнителе.
Правильно оформленные строки включают выражения, такие как “Дождь выпадает в Испании главным образом на равнине”, “Неверный ввод: попробуйте число, меньше чем-5”, и “Отвечают требованиям по напряжению”. Строка в SMath Studio, в то время как имеет неограниченный размер, всегда появляется как одна линия текста в Вашем рабочем листе. Отметьте, что строка такая как “123,” созданная путем, описанном выше, как понимает Mathcad, является строкой цифр, а не числом 123.
Строки особенно полезны для генерации сообщений об ошибке в программах, как описано в Главе 15, «Программирование». Другие функции обработки строки перечислены в разделе «Строковые функции». Используйте строки также, чтобы определить системные пути для аргументов некоторых встроенных в SMath Studio функций; см. “Функции Доступа к файлу”.
Имя в SMath Studio — просто последовательность цифр, которые Вы печатаете или вставляете в математическую область. Имя обычно обращается к переменной или функции, которую Вы используете в своих вычислениях. SMath Studio различает два вида имен:
Встроенные имена, которые являются названиями переменных и функций, которые всегда доступны в SMath Studio, и которые Вы можете использовать свободно в создании математических выражений;
Имена, определенные пользователем, которые являются названиями переменных и функций, которые Вы создаете в своих рабочих листах SMath Studio.
Поскольку SMath Studio — окружающая среда для числового и символического вычисления, большое количество имен встроены в программу для использования в математических выражениях. Эти встроенные имена включают встроенные переменные и встроенные функции .
SMath Studio включает несколько переменных, которые, в отличие от обычных переменных, уже определены, когда Вы запускаете SMath Studio. Эти предопределенные или встроенные переменные так же имеет обычное значение, как (3.14159. ) или e (2.71828. ), или используется в качестве системных переменных, чтобы управлять вычислениями в SMath Studio. См. “Встроенные Переменные” для дополнительной информации;
В дополнение к этим предопределенным переменным SMath Studio рассматривает названия всех встроенных единиц как предопределенные переменные. Например, SMath Studio опознает имя “A” как ампер, “m” как метр, “s” как секунда, и так далее. Выберите Единица измерения из меню Вставка , или нажмите
SMath Studio включает большое количество встроенных функций, которые позволяют производить различные действия в большом диапазоне от простых вычислений до вычерчивания сложной эмпирической кривой, работы с матрицами и статистике. Чтобы получить доступ к одной из этих встроенных функций, Вы можете выбрать Функция из меню Вставка или нажать
Имена переменных и функций, определяемые пользователем
SMath Studio позволяет Вам использовать большое разнообразие выражений как имена переменной или имена функции.
Имена в SMath Studio могут содержать любой из следующих символов:
большие или маленькие буквы;
цифры от 0 до 9;
символ подчеркивания (_);
главный символ (‘). Отметьте, что это не то же самое как апостроф. Вы узнаете, что главный символ вставляется по нажатию клавиши тильда (
греческие буквы. Чтобы вставить греческую букву, выберите нужный символ на панели инструментов Символы . Раздел «греческие буквы» на странице даст более детальную информацию;
символ бесконечности Арифметика или печатая [Ctrl] [Shift] Z.
Следующие примеры имен – верные
Следующие ограничения относятся к именам переменной:
Имя не может начаться с одной из цифр 0 до 9. SMath Studio интерпретирует что-либо начинающееся с цифры или как комплексное число (2 i );
Символ бесконечности не может быть первым символом в имени переменной;
Любые цифры, которые Вы печатаете после нажатия (.), появляются как подстрочные. Это обсуждено в “Подстрочных символах”;
SMath Studio не различает имена переменной и имена функции. Таким образом, если Вы определите f(x) , и позже Вы определяете переменную f , то Вы обнаружите, что не можете использовать f(x) нигде ниже определения для f ;
SMath Studio различает прописные и строчные буквы. Например, diam — переменная, отличная от DIAM .
Есть два способа ввести греческое имя переменной в SMath Studio:
Нажмите на соответствующий символ на панели инструментов Символы . Чтобы видеть эту панель инструментов, нажмите на кнопку
Напечатайте римский эквивалент греческого символа и затем нажмите [Ctrl] G . Например, чтобы войти в , нажмите f [Ctrl] G . См. «греческие буквы» в приложениях для таблицы греческих букв и их римских эквивалентов.
Хотя многие из заглавных греческих букв похожи на обычные заглавные буквы, они не одно и то же. SMath Studio различает греческие и римские символы, даже если они кажутся визуально эквивалентными.
Если Вы включаете точку в имя переменной, SMath Studio показывает то, что следует за точкой, как подстрочное. Вы можете использовать эти подстрочные символы , чтобы создать переменные с именами как vel init и u air .
Для получения подстрочных символов необходимо выполнить следующие шаги:
1. Напечатайте часть имени, которое расположено перед подстрочными символами
2. Напечатайте символ (.) перед частью имени, которая должна стать подстрочным символом.
Не путайте подстрочные символы приписки с индексами массива , которые получены нажатием левой скобки ([) или нажимая Функции . Хотя они отображаются подобно подстрочному символу – подстрочный символ появляется ниже линии, как индекс массива, но с небольшим пространством перед символом – они ведут себя вполне по-разному в вычислениях. Подстрочный символ – просто косметическая часть имени переменной. Индекс массива представляет ссылку на элемент массива. См. главу 11, “Векторы, Матрицы, и Массивы Данных,” для описания того, как использовать индексы для массивов.
Как описано в предыдущем разделе, определенные символы, как буквы и цифры, составляют части имен и чисел. Другие символы, как * и +, представляют “операторы «. Операторы – символы такие как“ +” и “-”, которые соединяют переменные и числа, чтобы сформировать выражения. Переменные и числа, соединенные операторами, называют операндами . Например, в выражении:
операндами для “+” являются x и y . Операнды для оператора показателя степени — a и выражение .
Вы печатаете общие арифметические операторы, используя стандартные нажатия клавиш, таких как * и +, используемый в Вашей электронной таблице и других приложениях. Но все операторы SMath Studio могут быть введены с помощью нажатий клавиш или щелкая кнопками на панелях инструментов. Например, Вы вводите оператор квадратного корня в SMath Studio, печатая или нажимая Арифметика . См. «Операторы» в Приложениях для полного списка операторов. Операторы SMath Studio также обсуждены подробно в Главе 9, «Операторы».
4.2 Составление выражений
Вы можете создать много математических выражений, просто печатая набор цифр, или вводя соответствующие операторы с панелей инструментов.
| Например, если вы наберете символы |
вы получите результат, показанный справа
С первого взгляда, редактор уравнения SMath Studio очень походит на простой редактор текста, но является большим, чем текстовый редактор. У математических выражений есть четкая структура, и редактор уравнения SMath Studio специально разработан, чтобы работать в пределах той структуры. В SMath Studio математические выражения строятся не так, как они напечатаны.
SMath Studio автоматически собирает различные части, которые составляют выражение, используя правила старшинства и некоторые дополнительные правила, которые упрощают вход в знаменатели, показатели степени, и подкоренные выражения. Например, когда Вы при наборе выражения печатаете / или нажимаете Арифметика , чтобы создать дробь, SMath Studio остается в знаменателе, пока Вы не нажимаете [Пробел], чтобы выбрать все выражение.
Набор имен и чисел
Когда Вы печатаете на имена или числа, SMath Studio ведет себя очень как стандартный текстовой процессор. Когда Вы печатаете, Вы видите, что цифры, которые Вы печатаете, появляются позади вертикальной линии редактирования . Левые и правые клавиши курсора перемещают эту вертикальную линию редактирования налево или направо на один символ за один раз, так же, как если бы они были бы в текстовом редакторе. Есть, однако, два важных различия:
1. Если вы перемещаете курсор направо, вертикальная линия редактирования оставляет позади след. Этот след — “горизонтальная линия редактирования.” Ее значимость становится очевидной, когда Вы начинаете работать с операторами.
2. Если у уравнения, в котором Вы уже щелкнули, нет оператора, нажатие клавиши [ Пробел ] превращает математическую область в текстовую область. Невозможно вернуть текстовую область обратно в математическую область.
Ключ к работе с операторами состоит в умении определять, какая переменная или выражение должны стать операндом . Есть два способа сделать это:
Вы можете напечатать оператор сначала и заполнить метки-заполнители с операндами, или
Вы можете использовать линии редактирования, чтобы определить, какую переменную или выражение Вы хотите превратиться в операнд
Первый метод больше похож на то, что Вы строите скелет и заполняете детали позже. Этот метод может быть легко использовать, когда Вы строите очень сложные выражения, или когда Вы работаете с такими операторами как суммирование, которые требуют многих операндов, но не имеют естественного порядка печатания.
Второй метод больше напоминает прямое печатание и может быть намного быстрее, когда выражения просты. Практически, Вы можете переключиться назад и вперед, если возникает потребность.
Вот каким образом составляется выражение, используя первый метод:
1. Нажмите ^, чтобы создать оператор показателя степени, или нажмите Арифметика . Вы видите две метки-заполнителя. Линии редактирования «держат» метку-заполнитель основания.
2. Наберите а , и щелкните левой кнопкой мыши в области символа а
3. Щелкните левой мыши в метку-заполнитель показателя степени
5. Щелкните левой кнопкой мыши перед знаком + и наберите х , затем щелкните левой кнопкой мыши в метку-заполнитель после + и наберите у
При использовании линий редактирования, чтобы создать выражение , выполните следующие действия:
1. Наберите a . Линии редактирования держат а , оно становится первым операндом любого оператора, который Вы затем печатаете.
2. Нажмите ^ , чтобы создать оператор показателя степени. Как обещалось, а становится первым операндом показателя степени. Линии редактирования теперь держат другую метку-заполнитель.
3. Наберите х+у в метке-заполнителе для завершения выражения
Отметьте, что в этом примере, Вы могли напечатать выражение тем же самым путем, как Вы говорите его вслух. Однако, даже этот простой пример уже содержит двусмысленность. Когда Вы говорите “x плюс y” нет никакого способа сказать, имеете ли Вы в виду или . Для более сложных выражений число двусмысленностей резко увеличивается.
Хотя Вы можете всегда решать проблему двусмысленности использованием круглых скобок, подобное решение могут быстро стать тяжелыми. Лучший путь состоит в том, чтобы использовать линии редактирования, чтобы определить операнды любого оператора, который Вы печатаете. Следующий пример иллюстрирует это, описывая, как создать выражение вместо .
1. Наберите a ^ x , как Вы сделали в предыдущем примере. Отметьте, как линии редактирования держат располагаются между x. Если бы Вы должны были напечатать + в этой точке, x стал бы первым операндом операции «плюс».
2. Нажмите [Пробел]. Линии редактирования теперь держат все выражение .
3. Теперь напечатайте +. Независимо от того, что находилось между линиями редактирования, оно теперь становится первым операндом операции «плюс».
4. В появившейся метке-заполнителе наберите y .
Распространенный способ показать умножение между двумя переменными на листке бумаги состоит в том, чтобы разместить их друг рядом с другом. Например, выражения как ax или , как легко понимают, означают “ a умножить на x ” и “ а умножить на x плюс y ” соответственно. Это не может быть сделано с переменными SMath Studio по простой причине, что, когда Вы печатаете ax , у SMath Studio нет никакого способа знать, имеете ли Вы в виду “ a умножить на x ” или “переменную, названную ax .” Точно так же, когда Вы набираете a(x+y) , не может сказать SMath Studio, имеете ли Вы в виду “ а умножить на x плюс y ”, или имеете ли Вы в виду “функцию а с аргументом x+y”.
Чтобы избежать двусмысленности в Вашей каждодневной работе, мы рекомендуем, чтобы Вы всегда нажимали * явно, чтобы указать на умножение, как показано в следующем примере:
1. Напечатайте a сопровождаемое *. SMath Studio вставляет небольшую точку после “ a ”, чтобы указать на умножение.
2. В появившейся метке-заполнителе наберите второй множитель x
В частном случае, когда Вы печатаете число, сопровождаемое немедленно именем переменной, например 4x , SMath Studio интерпретирует выражение, чтобы означать число, умноженное на переменную: . SMath Studio показывает точку между числом и переменной, чтобы указать, что умножение подразумевается. Таким образом, Вы можете произвести математическую систему обозначений, которая близко аппроксимирует систему обозначений, которую Вы видите в учебниках и справочниках. Кроме того, SMath Studio резервирует определенные символы, такие как “ i ” для мнимой единицы, как суффикс для чисел, и если вы напишите 2i , то в этом случае увидите на экране , хотя это не будет рассматриваться как умножение числа на переменную.
Пример с описанием
Когда дело доходит до редактирования уравнений, знание того, как использовать линии редактирования, принимает значимость, подобную знанию, куда поместить мигающий вертикальный прямоугольник (точка вставки), который Вы видите в большинстве текстовых процессоров. Текстовой процессор может использовать простой вертикальный прямоугольник, потому что текст является всегда одномерным, как линия. Новые символы идут или слева или справа от старых. Уравнение, с другой стороны, действительно двумерно, однако его структура больше похожа на дерево с ветвями, чем подобный линии текст. В результате SMath Studio должен использовать двумерную версию того же самого вертикального прямоугольника. Именно поэтому есть две линии редактирования: вертикальная линия и горизонтальная линия.
Предположите, например, что Вы хотите напечатать немного более сложное выражение
Наблюдайте то, что происходит с линиями редактирования в следующих шагах:
1. Напечатайте x-3*a^2 . Так как линии редактирования охватывают только цифру «2», только эта цифра “2” становится числителем, когда Вы нажимаете /. Так как мы хотим, чтобы целое выражение было числителем, мы должны заставить линии редактирования охватить все выражение.
2. Чтобы сделать так, нажмите [Пробел]. Каждый раз, когда Вы нажимаете [Пробел], линии редактирования охватывают все большую часть выражения. Вы должны нажать [Пробел] три раза, чтобы охватить все выражение.
3. Теперь нажмите / чтобы создать дробную черту. Отметьте, что числитель — то, что было охвачено линиями редактирования, когда Вы нажали /.
4. Теперь набираем -4 + и нажимаем Арифметика . Тогда набираем y+1 под корнем, чтобы закончить знаменатель.
5. Чтобы прибавить что-то вне знака корня, нажмите [Пробел] дважды, чтобы заставить линии редактирования охватить корень. Например, чтобы прибавить число к знаменателю, нажмите [Пробел] дважды.
6. Нажмите +. Так как линии редактирования охватывают весь корень, то весь корень становится первым операндом, когда Вы нажимаете +.
4.3 Редактирование выражений
Этот раздел описывает, как произвести изменения в существующем выражении.
Изменение имени или числа
Для редактирования имени или числа:
Нажмите на него мышью. Это помещает вертикальную линию редактирования, где Вы щелкали мышью.
Переместите вертикальную линию редактирования в случае необходимости, нажимая клавиши горизонтального перемещения курсора.
Если Вы печатаете цифру, она появляется только слева от вертикальной линии редактирования. Нажатие [ Backspace ] удаляет цифру слева от вертикальной линии редактирования. Нажатие [ Delete ], удаляет цифру справа от вертикальной линии редактирования.
Легче всего ввести оператор между двумя символами в имени или двумя числами в постоянной. Например, вот как вставить плюс знак между двумя цифрами:
1. Поместите линии редактирования там, где Вы хотите, чтобы был знак плюс.
2. Нажмите клавишу + или нажмите кнопку Арифметика
Вы никогда не должны вставлять пробел, печатая уравнение. Пробел вставляется SMath Studio автоматически вокруг операторов везде, где это необходимо. Если Вы действительно пытаетесь вставить пробел, SMath Studio предполагает, что Вы хотели печатать текст, а не математику и преобразовываете свою математическую область в текстовую область соответственно.
Операторы, такие как деление и возведение в степень приводят к более значительным изменениям форматирования. Например, когда Вы вставляете знак деления, SMath Studio перемещает все, что находится после знака деления в знаменатель. Вот то, как Вы вставляете знак деления:
1. Поместите линии редактирования туда, где Вы хотите, чтобы был знак деления.
2. Нажмите клавишу / или нажмите Арифметика . SMath Studio переформатировал выражение, чтобы приспособить деление.
Некоторые операторы требуют только одного операнда. Примеры — квадратный корень, абсолютное значение (модуль), и операторы сопряженного комплексного числа. Чтобы вставить один из них, поместите линии редактирования по обе стороны от операнда и нажмите соответствующее нажатие клавиши. Многие из этих операторов доступны также на панели инструментов Арифметика . Например, чтобы преобразовать x в делают следующее:
1. Поместите линии редактирования рядом с «x», перед или после символа.
2. Нажмите , чтобы ввести оператор квадратного корня, или нажмите Арифметика .
Добавление оператора в выражение
Методы, описанные в предыдущей части раздела, наиболее очевидны, когда Вы хотите добавить оператор к переменной или числу. Если Вы хотите добавить оператор ко всему выражению, есть два способа для этого:
Окружите то выражение круглыми скобками и продолжите двигаться как описано в предыдущем разделе, или
Используйте линии редактирования, чтобы определить выражение, к которому Вы хотите применить оператор.
Хотя первый метод может быть более интуитивным, это медленнее, так как Вы должны напечатать пару круглых скобок. Более эффективный второй метод — предмет этого раздела. Разделы “Вставка круглых скобок” и “Удалении круглых скобок” описывают способы работать с круглыми скобками более эффективно.
Линии редактирования состоят из горизонтальной линии и вертикальной линии, которая перемещается слева направо вдоль горизонтальной линии. Чтобы вставить оператор в выражение, выберите выражение, помещая его между двумя линиями редактирования. Следующие примеры показывают, что результат печатания * c даст абсолютно различных выражения в зависимости от того, что было выбрано.
Здесь, две линии редактирования охватывают только числитель. Это означает, что любой оператор, который Вы печатаете, будет применим только к числителю.
Печатание *c приводит к данному выражению. Отметьте, что выражение, которое находилось между линиями редактирования, стало первым операндом умножения.
Здесь, линии редактирования охватывают все выражение. Это означает, что любой оператор, который Вы печатаете, будет относиться ко всему выражению.
Печатание *c приводит к данному выражению. Отметьте, как все, что было охвачено линиями редактирования стало первым операндом умножения.
Здесь, линии редактирования охватывают все выражение, как они делали это в предыдущем примере. Однако, на сей раз вертикальная линия редактирования находится на левой стороне вместо правой стороны.
Печатание *c приводит к данному выражению. Отметьте, как выражение, охваченное линиями редактирования, стало вторым, а не первым операндом умножения. Это произошло, потому что вертикальная линия редактирования была на левой стороне, а не правой стороне.
Управление линиями редактирования
Вы используете следующие методы, чтобы управлять тем, как располагаются линии редактирования:
Нажмите на оператор. В зависимости от того, где на операторе Вы щелкаете, Вы найдете вертикальную линию редактирования или слева или справа от оператора, с горизонтальной линией, выбирающей операнд оператора. Если Вы хотите переместить вертикальную линию редактирования от одной стороны до другого в настоящее время отбираемого выражения, нажмите клавиши [Home] либо [End].
Используйте клавиши горизонтального перемещения курсора, чтобы переместиться, вертикальное редактирование перемещается на один символ за один раз. Горизонтальная линия редактирования выбирает операнд самого близкого оператора. Если Ваше выражение содержит составные части, Вы можете также использовать клавиши вертикального перемещения курсора, чтобы переместить линии редактирования.
Нажмите [ Пробел ], чтобы выбрать каждый раз все большие части выражения, которые будут охвачены линиями редактирования. Каждый раз, когда Вы нажимаете [ Пробел ], линии редактирования охватывают все большие части выражения, пока в конечном счете они не охватывают все выражение. Нажатие [ Пробел ] еще раз возвращает линии редактирования туда, где они были, когда Вы начали.
Следующий пример показывает вам короткий цикл посредством использования [ Пробел ]:
1. Это — стартовая позиция. Две линии редактирования охватывают только единственную переменную «d».
2. Нажатие [ Пробел ] заставляет линии редактирования измениться так, чтобы они теперь охватывают весь знаменатель.
3. Однократное нажатие [ Пробел ] заставляет линии редактирования измениться снова так, чтобы они теперь охватывали все выражение.
4. В этой точке линии редактирования не могут стать больше. Нажатие [ Пробел ] перемещает линии редактирования вверх.
Вы заметите, что в продвижении через предыдущий цикл никогда не было промежуточного шага, в котором линии редактирования держали только a или только b в числителе. Поэтому последовательность шагов, которые проходят линии редактирования, когда Вы нажимаете [ Пробел ], зависит от отправной точки цикла.
Чтобы установить отправную точку цикла, или нажмите на соответствующую часть выражения как описано ранее, или используют клавиши курсора, чтобы переместить выражение. Клавиши курсора перемещают линии редактирования через выражение в обозначенном направлении. Имейте в виду, однако, что нажатие клавиш «вверх» и «вниз» или «влево» и «вправо», возможно, не всегда приведут к очевидным результатам, особенно когда выражение становится очень сложным или если имеется возведение в степень, суммирование, интегралы, и другие достаточно сложные операторы.
Редактирование строк отличается от редактирования других математических выражений, потому что Вы должны использовать клавиши курсора или щелчок вне строки, чтобы выйти из строки. Нажатие [ Пробел ], которое может быть использовано в других выражениях, чтобы изменить положение линий редактирования, интерпретируется как только другой символ в строке.
Чтобы удалить оператор, соединяющий два имени переменных или две константы:
1. Поместите вертикальную линию редактирования после оператора.
2. Нажмите [ Backspace ] дважды
Теперь Вы можете легко ввести новый оператор, чтобы заменить тот, который Вы только что удалили, печатая этот оператор.
В вышеупомянутых примерах легко видеть, что «перед» и «после» условны, потому что выражения, возведенные в степень естественно, идут слева направо, по тому же самому способ, которым мы их читаем. Дроби ведут себя точно так же. Так как мы обычно говорим “ а разделить на b ,” для помещения линий редактирования «после» знака деления, нужно помещать их как раз перед b . Точно так же для помещения линий редактирования «перед» знаком деления, нужно помещать их сразу после a . Следующий пример иллюстрирует это:
1. Поместите вертикальные линии редактирования после знака деления.
2. Нажмите [ Backspace ] дважды
Удалить оператор, имеющий только один операнд (например , или ) без удаления самого выражения, которое стоит в операторе, в SMath Studio невозможно.
Чтобы заменить оператор после удаления этого оператора, находящегося между двумя переменными или константами или рядом с одной переменной, как показано выше, просто печатают новый оператор после нажатия [ Backspace ].
Для замены оператора между двумя выражениями:
1. Поместите линии редактирования сразу после оператора.
2. Нажмите [ Backspace ]. Появляется метка-заполнитель для вставки оператора.
3. Введите новый оператор
Вставка знака минус
Знак минус, который означает «отрицание», использует то же самое нажатие клавиши, которую используют для действия «вычитают». Для определения, что вставить, SMath Studio смотрит на то, где вертикальная линия редактирования. Если это слева, SMath Studio вставляет знак минус, обозначающий «отрицание». Если это справа, SMath Studio вставляет знак минус, обозначающий «вычитание».
Следующий пример показывает, как вставить минус знак перед “sin( a )”.
1. Нажмите на sin(a). В случае необходимости, нажмите [ Пробел ], чтобы выбрать все выражение.
2. В случае необходимости, нажмите клавиши управления курсором, чтобы переместить вертикальную линию редактирования максимально налево.
3. Напечатайте — или нажмите Арифметика , чтобы вставить знак минус.
Если Вы хотите перейти от sin(a) к 1-sin(a), введите другой оператор (например, “+”), как описано в разделе “Вставка Оператора”. Затем замените оператор на знак минус как описано в разделе “Удаление Оператора”.
Когда Вы заменяете оператор, и показана метка-заполнитель оператора, выберите выражение, а не единственную переменную, справа от метки-заполнителя оператора и нажмите — чтобы поместить знак минус вычитание в метку-заполнитель. Иначе SMath Studio вставляет знак отрицания.
Вставка круглых скобок
SMath Studio помещает круглые скобки автоматически из-за необходимости поддержать предшествующие операции. Могут быть случаи, однако, когда Вы хотите поместить круглые скобки, чтобы разъяснить выражение или изменить полную структуру выражения. Вы не можете вводить круглые скобки по одной, возможно ввести только пару круглых скобок. Это сделано для избежании возможности несовпадающих круглых скобок.
Для ввода круглых скобок в имеющееся выражение:
1. Выберите выражение и поместите его между линиями редактирования. Сделайте это, нажав на выражение и нажимая [ Пробел ] один или более раз.
2. Нажмите (, или нажмите Арифметика . Отобранное выражение теперь заключено между круглыми скобками.
Удаление круглых скобок без удаления содержащегося в них выражения в SMath Studio невозможно.
Добавление функций в выражения
Чтобы превратить выражение в аргумент функции, сделайте данные шаги:
1. Щелкните в выражении и нажимайте [ Пробел ], пока все выражение не окажется между линиями редактирования.
2. Нажмите (, или нажмите Арифметика . Отобранное выражение теперь заключено между круглыми скобками.
3. Нажмите [ Пробел ]. Линии редактирования теперь охватывают также и круглые скобки.
4. Используя клавиши управления курсором, сделайте так, чтобы вертикальная линия редактирования переместилась на левую сторону. Если вертикальная линия редактирования уже находится на левой стороне, пропустите этот шаг.
5. Теперь введите имя функции. Если функция, которую Вы хотите использовать, является встроенной функцией, Вы можете также выбрать Функция из меню Вставка или нажать
Перемещение частей выражений
Команды меню Вырезать , Копировать и Вставить из меню Правка полезны для редактирования сложных выражений. Они функционируют следующим образом:
Вырезать ( [Ctrl] X на клавиатуре) удаляет то, что между линиями редактирования и копирует это в буфер обмена;
Копировать ( [Ctrl] C на клавиатуре) берет то, что между линиями редактирования и копирует это в буфер обмена;
Вставить ( [Ctrl] V на клавиатуре) берет то, что находится в буфере обмена и помещает его на Ваш рабочий лист, или в метку-заполнитель или в свободное место между другими областями.
Команды Копировать и Вставить используют буфер обмена, чтобы переместить выражения из одного места в другое.
Удаление частей выражения
Вы можете удалить часть выражения либо используя клавишу [ Delete ], либо используя клавиши [ Backspace ]. Если Вы используете этот метод, независимо от того, что Вы удаляете, не будет помещено в буфер обмена. Это полезно, когда Вы намереваетесь заменить то, что Вы удаляете, независимо от того, что в настоящее время находится в буфере обмена.
Чтобы удалить часть выражения, не помещая его в буфер обмена:
1. Выделите часть выражения (в данном случае числитель) так, чтобы оно было отображено на экране в инверсном цвете.
2. Нажмите [ Delete ] или [ Backspace ]. Это удалит числитель и оставляет на его месте метку-заполнитель.
Если Вы выбираете выражение с линиями редактирования вместо выделения как показано выше, Вы должны нажать [ Backspace ] несколько раз, чтобы удалить его. В этом случае, [ Backspace ] удаляет символы слева от линий редактирования.
Видео:решение уравнений и систем уравнений в SmathСкачать

Обзор доступных библиотек для численного решения жёстких ОДУ
Создавая дополнения к отечественной математической программе SMath Studio, я нашёл в сети ряд библиотек, которые можно было бы использовать в своих программах. Предлагаю небольшой их обзор.
Стандартный RK45 с фиксированным шагом может помочь в большинстве случаев, но бывают задачи, где этого недостаточно. Для решения жёстких систем были придуманы специальные решатели, которые мы и рассмотрим с точки зрения их практического использования.
Большинство представленных ниже функций, если не оговорено особо, можно привести к одному формату вызова (по аналогии с Mathcad):
где:
- init — вектор начальных условий,
- (x1, x2) — отрезок интегрирования,
- intvls — количество интервалов на отрезке,
- D(t, x) — система ОДУ.
1. Intel ODE Solvers Library
Содержит следующие функции: rkm9st(), mk52lfn(), mk52lfa(), rkm9mkn(), rkm9mka().
- rkm9st() — a specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.
- mk52lfn() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.
- mk52lfa() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.
- rkm9mkn() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.
- rkm9mka() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.
Библиотека написана на C со всеми вытекающими отсюда зависимостями. Доступны 32- и 64-разрядные версии библиотеки (libiode_ia32.lib и libiode_intel64.lib).
Дополнение ODE Solvers демонстрирует работу с этой библиотекой из c# кода.
2. GNU Scientific Library (GSL)
Содержит следующие функции: rk2(), rk4(), rkf45(), rkck(), rk8pd(), rk1imp(), rk2imp(), rk4imp(), bsimp(), msadams(), msbdf().
Часть из них требует дополнительные параметры для работы (Якобиан). Те, которые мне удалось привести к общему виду:
Solvers for Non-Stiff Systems:
- rk2() — explicit embedded Runge-Kutta (2, 3) method.
- rk4() — explicit 4th order (classical) Runge-Kutta. Error estimation is carried out by the step doubling method.
- rkf45() — explicit embedded Runge-Kutta-Fehlberg (4, 5) method.
- rkck() — explicit embedded Runge-Kutta Cash-Karp (4, 5) method.
- rk8pd() — explicit embedded Runge-Kutta Prince-Dormand (8, 9) method.
Остальные:
- rk1imp() — Implicit Gaussian first order Runge-Kutta. Also known as implicit Euler or backward Euler method. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- rk2imp() — Implicit Gaussian second order Runge-Kutta. Also known as implicit mid-point rule. Error estimation is carried out by the step doubling method. This stepper requires the Jacobian.
- rk4imp() — Implicit Gaussian 4th order Runge-Kutta. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- bsimp() — Implicit Bulirsch-Stoer method of Bader and Deuflhard. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
- msadams() — A variable-coefficient linear multistep Adams method in Nordsieck form. This stepper uses explicit Adams-Bashforth (predictor) and implicit Adams-Moulton (corrector) methods in P(EC)^m functional iteration mode. Method order varies dynamically between 1 and 12.
- msbdf() — A variable-coefficient linear multistep backward differentiation formula (BDF) method in Nordsieck form. This stepper uses the explicit BDF formula as predictor and implicit BDF formula as corrector. A modified Newton iteration method is used to solve the system of non-linear equations. Method order varies dynamically between 1 and 5. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
Для работы с функциями используется универсальный интерфейс, где конкретный тип решателя задаёт шаговую функцию. Дополнение GNUScientificLibrary демонстрирует работу с этой библиотекой из c# кода.
Не так просто сделать сборку библиотеки под Windows. Я использовал инструкцию с одного сайта, который сейчас недоступен. Тем не менее, в репозитории дополнения вы сможете найти 32- и 64-разрядные версии dll lib для GSL 1.16. Там находится вся библиотека, а не только решатели ОДУ.
3. Matlab C++ Math Library 2.1 (Win32)
28 Мб в развёрнутом виде) рядом со своей программой. Правда при вызове функций придётся использовать SetCurrentDirectory() с прямым указанием на место расположения «binwin32». Я так делаю в своём дополнении.
Содержит следующие функции: ode23(), ode45(), ode113(), ode15s(), ode23s().
- ode23() — solve nonstiff differential equations; low order method,
- ode45() — solve nonstiff differential equations; medium order method,
- ode113() — solve nonstiff differential equations; variable order method,
- ode15s() — solve stiff differential equations and DAEs; variable order method,
- ode23s() — solve stiff differential equations; low order method.
Дополнение MatlabCppMathLibrary демонстрирует работу с этой библиотекой из c# кода.
4. Octave C++ Math Library (Win32)
Примерно то же самое, что и Matlab C++ Math Library, но со своими тараканами. К сожалению, работу с этой библиотекой я одолел только частично. Дополнение OctaveCppMathLibrary демонстрирует работу с этой библиотекой из c# кода.
5. DotNumerics
Содержит следующие функции: AdamsMoulton(), ExplicitRK45(), ImplicitRK5(), GearsBDF(). Эта библиотека портирована для .Net с фортрана. Она понравилась мне больше всего. Работает достаточно быстро.
Solvers for Non-Stiff Systems:
- AdamsMoulton() — solves an initial-value problem for nonstiff ordinary differential equations using the Adams-Moulton method.
- ExplicitRK45() — solves an initial-value problem for nonstiff ordinary differential equations using the explicit Runge-Kutta method of order (4)5.
Solvers for Stiff Systems:
- ImplicitRK5() — solves an initial-value problem for stiff ordinary differential equations using the implicit Runge-Kutta method of order 5.
- GearsBDF() — solves an initial-value problem for stiff ordinary differential equations using the Gear’s BDF method.
Имеется много перегрузок для различных форматов вызова функций. Дополнение DotNumerics демонстрирует работу с этой библиотекой.
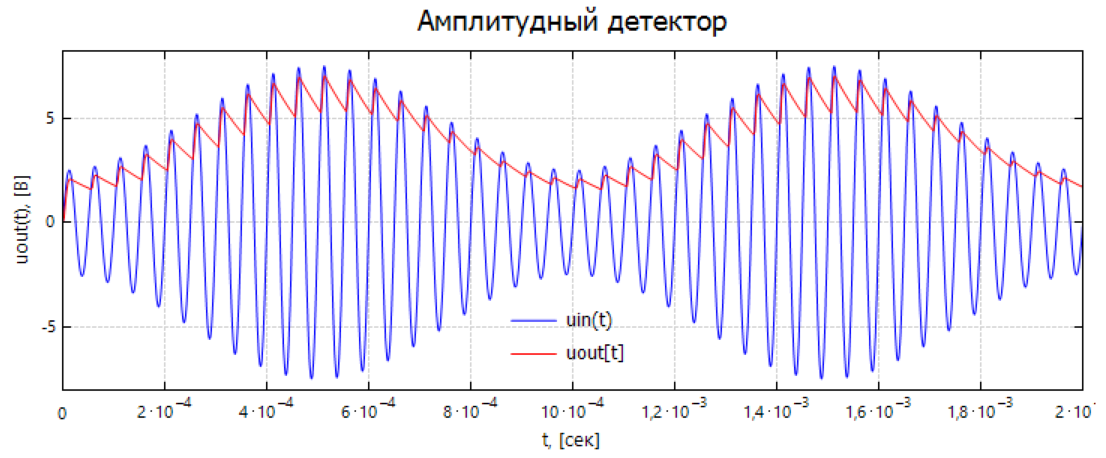
Как выглядит модель амплитудного детектора в SMath Studio при решении ОДУ с помощью функции GearsBDF():
Обновление (12.07.2014).
6. boost::odeint
Содержит следующие алгоритмы:
- Explicit Euler
- Modified Midpoint
- Runge-Kutta 4
- Cash-Karp
- Dormand-Prince 5
- Fehlberg 78
- Adams Bashforth
- Adams Moulton
- Adams Bashforth Moulton
- Controlled Runge-Kutta
- Dense Output Runge-Kutta
- Bulirsch-Stoer
- Bulirsch-Stoer Dense Output
- Implicit Euler
- Rosenbrock 4
- Controlled Rosenbrock 4
- Dense Output Rosenbrock 4
- Symplectic Euler
- Symplectic RKN McLachlan
- Symplectic RKN McLachlan
Живьём не пробовал, показать пример использования не могу.
7. SADEL (Sets of Algebraic and Differential Equations solvers Library)
Живьём не пробовал, показать пример использования не могу.
8. Решатель Лимонова А. Г.
Живьём не пробовал, показать пример использования не могу.
📹 Видео
Решение СЛАУ в SMathСкачать

SMatch Studio - 05. Поиск корней rootsСкачать

Решение математических задач в программе SMath StudioСкачать

СР РЕШЕНИЕ УРАВНЕНИЙСкачать

Как вводить выражения в SMath StudioСкачать

Решение СЛУ в SMathСкачать

Smath Studio & LibreCAD практика 2 урок "Рассчитываем таблицу"Скачать

Матрицы в SMath StudioСкачать

График функции в SMath StudioСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Mathcad-09. Пример: уравненияСкачать

Графическое представление данных и функций в SMath и PrimeСкачать

SMath Studio - Урок 8 - Работа с матрицамиСкачать

Как решают уравнения в России и США!?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

SmathStudio программа для математических расчетовСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Решение уравненийСкачать