Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).
Универсальное множество (универсум) U — множество, содержащее все элементы рассматриваемых подмножеств и элементы, не входящие в них.
Пустое множество Ø — множество, не содержащее ни одного элемента рассматриваемых подмножеств.
Количество пересечений (областей) n определяется по формуле: n=2 N ,
где N — количество множеств.
- Рисование кругов Эйлера
- Алгоритм построения диаграмм Эйлера-Венна
- Диаграммы Эйлера-Венна для одного множества А
- Диаграммы Эйлера-Венна для двух множеств А и В
- Диаграммы Эйлера-Венна для трех множеств А , В , С
- Диаграммы Эйлера-Венна для четырех множеств А , В , С , D
- Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
- Решить уравнение теории множеств и отобразить на диаграмме эйлера венна
- Множества на диаграмме Эйлера-Венна и ее практическое применение
- Круги Эйлера — примеры и методы решения логических задач
- Множества в математике
- Отношения между понятиями
- Решение задач, примеры
- 🌟 Видео
Видео:Доказать равенства при помощи диаграмм ВеннаСкачать

Рисование кругов Эйлера
Видео:Круги Эйлера. Логическая задача на множества. Иностранные языкиСкачать

Алгоритм построения диаграмм Эйлера-Венна
- Определяют количество подмножеств ( А , В , С , D ).
- На диаграмме строят пересекающиеся множества, включенных в универсум.
- Выделяют области, количество которых равно количеству пересечений.
Видео:Доказать равенства при помощи диаграмм Эйлера-Венна. Действия над множествами.Скачать

Диаграммы Эйлера-Венна для одного множества А
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 1 = 2 строк (областей)
Примеры
Универсум U=, А=
A = , A ∩ A = ∩ = = Ø
Видео:Множества и операции над нимиСкачать

Диаграммы Эйлера-Венна для двух множеств А и В
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 2 = 4 строк (областей)
Примеры
Универсум U=, А=, В=
A∪B = ∪ =
Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Диаграммы Эйлера-Венна для трех множеств А , В , С
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 3 = 8 строк (областей)
Примеры
Универсум U=, А=, В=, C=
BC ∪ A = ∪ = ∪ =
Видео:Операции над множествамиСкачать

Диаграммы Эйлера-Венна для четырех множеств А , В , С , D
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=2 4 = 16 строк (областей)
Примеры
Универсум U=
А=
В=
C=
D=
Видео:Простое объяснения решения задач при помощи кругов ЭйлераСкачать

Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2 n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис.5 

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Для каждого запроса построим диаграмму Эйлера-Венна:
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14 человек, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек — и математический и физический, 5 и математический и химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ — множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
| Круги Эйлера с названиями непересекающихся множеств: |
Например, количество человек, которые посещают физический кружок 2+6+1+5=14
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре — 11, в цирке 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре и в цирке — 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:
Аналогично, только в кино и цирке (10-х) чел.
Только в театре и цирке (4-х) чел.
В кино побывало 25 чел., значит, из них только в кино были 25 — (10-х) – (6-х) – х = (9+х).
Аналогично, только в театре были (1+х) чел.
Только в цирке были (3+х) чел.
Не были в театре, кино и цирке – 2 чел.
Значит, 36-2=34 чел. побывали на мероприятиях.
С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке:
Отсюда следует, что только один человек побывал на всех трех мероприятиях.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Видео:Как изображать множества на диаграммахСкачать

Решить уравнение теории множеств и отобразить на диаграмме эйлера венна
Видео:Теория. Числовые множества. Диаграмма Эйлера-Венна (5-11 класс)Скачать

Множества на диаграмме Эйлера-Венна и ее практическое применение
Автор работы награжден дипломом победителя II степени
Множества встречаются в различных областях знаний: математике, физике, биологии, химии, лингвистике и т.д. Множества состоят из различных элементов, например, страны, дома, птицы, числа, фигуры, точки и т.д. В математике множество рассматривается в каждой задаче: алгебраические выражения, решение уравнений, неравенств, систем уравнений, систем неравенств, любые текстовые задачи, функции, расположение множества точек, геометрические задачи, логика, статистика, вероятность и т.д.
При решении большинства задач на множество применяют диаграмму Эйлера-Венна, поэтому данная тема очень актуальна в области математики.
Цель работы: изучить множества и действия над ними, рассмотреть решение практических задач на множество с применением диаграммы Эйлера-Венна, провести исследование среди учащихся 7-9 классов и смоделировать макет по множествам в 3 D формате .
Для достижения цели необходимо выделить следующие задачи исследования:
— изучение понятия множества;
— определение видов множества ;
— рассмотрение действий над множествами;
— изучение диаграммы Эйлера-Венна;
— решение задач на множества с применением диаграммы Эйлера-Венна;
— использование диаграммы Эйлера-Венна при исследовании;
Гипотеза: зная понятие множества и решение их с помощью диаграммы Эйлера-Венна приведет к упрощению решения задач и к сокращению времени на их выполнение, а применение его покажет и докажет востребованность в сравнении и нахождении неизвестного множества.
Объект исследования: Множества.
Предмет исследования: Множества на диаграмме Эйлера-Венна.
Работа состоит из теоретической, практической и исследовательской части. В теоретической части раскрыт вопрос о множествах, видах множества, действиях над ними и что представляет собой диаграмма Эйлера-Венна, а также различие кругов Эйлера и Венна. В практической части приведены решения пяти авторских сложных задач на множества с помощью кругов Эйлера-Венна. В исследовательской части проводится анкетирование среди учащихся 7-9 классов. Анализируя данные анкеты составляются диаграммы для решение определенных вопросов. Моделируется на 3 D принтере макет из трех множеств .
1. Теоретические аспекты множества
1.1. Что такое множество?
Впервые изучение бесконечных множеств и множеств в неявной форме рассматривалось ещё в Древней Греции. Затем множества встречались в первых идеях Галилео Галилея, а также в начале 1800-х годов в работах Гаусса как бесконечное множество. Создатель теории множеств немецкий математик Георг Кантор (1845-1918гг). Его многочисленные работы были опубликованы в период с 1872 года по 1897 год. Георг Кантор говорил, что «Множество есть многое, мыслимое нами как единое». [1]
Георг Кантор (1845-1918гг) немецкий математик
К сожалению, нет точного определения множества, только описательное объяснение.
Множество – это совокупность каких-либо объектов с определенными характеристическими свойствами. Объекты множества называются элементами множества . Множество может состоять из различных элементов – здания, книги, ученики, числа, фигуры и т.д. Множества обозначаются заглавными буквами А, В, С и т.д., а элементы множества маленькими буквами а, в, с и т.д. латинского алфавита и записываются в фигурных скобках, например, А = .
Принадлежность элемента к множеству записывается в следующем виде: ϵ А и читается: « принадлежит множеству А», где А – множество, – элемент множества А, ϵ — знак «принадлежит». Например, в библиотеке находится N количество книг, библиотека является множеством, а любая книга в библиотеке будет элементом этого множества.
Кроме множества есть такое понятие как подмножество. Некоторое множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В и обозначается А ⊆ В. Например, допустим, в школе учатся 1000 учащихся, а в 8 -х классах учатся 147 учеников. Значит, учащиеся 8 класса являются подмножеством множества школы.
Следующее понятие множества — мощность множества. Мощность множества – это количество одинаковых элементов во множестве и обозначается: |С| или n ( C ) — мощность множества С.
Например, в корзине для мячиков есть всего 5 одинаковых мячей, корзина это множество, а 5 одинаковых мячей это мощность множества и запись имеет вид: n ( C ) = 5.
Существует различные виды множеств:
1. Пустое множество – это множество, в котором нет элементов. Например, в кошельке нет денег и обозначается как К ϵ Ø.
2. Конечное множество – это множество, в котором содержится конечное число элементов. Например, количество страниц в книге 96, значит это конечное множество, т.е. К =
3. Бесконечное множество – это множество, в котором бесконечно много элементов. Например, количество чисел в последовательности Фибоначчи, т.е. Ф =
4. Универсальное множество – это множество, в которое входят все множества в качестве подмножества. Например, все числовые множества являются подмножеством действительных чисел или множество точек любой геометрической фигуры это подмножество в множестве всех точек геометрического пространства. Обозначается большой буквой Е. [2]
1.2. Действия над множествами
Над множеством, как и над любым понятием в математике, можно выполнить некие действия. Рассмотрим некоторые действия:
1. Пересечение множеств (произведение) – это новое множество, которое состоит из общего количества одинаковых элементов, входящих в каждое из нескольких множеств А, В, С, D . и обозначается , если дано два множества А и В, а новое множество С: С = A ⋂ B или С = А × В ↔ С = В ⋂ А или С = В × А. Изображение пересечения на рисунке 1.
а) A ⋂ B = С в ) A ⋂ B = с ) A ⋂ B = Ø
Рис. 1. Пересечение множеств А и В
Пример, ученики посещают спортивные секции: теннис, борьба, шахматы и верховая езда. Пересечением будет спортсмен, который посещает все секции.
Приведем пример из математики:
1) Даны множества М = и К = . Найти пересечение множеств.
Пересечением множеств М и К: М ⋂ К =
2) Даны множества М = и К = . Найти пересечение множеств.
Пересечением множеств М и К: М ⋂ К =
3) Даны множества М = и К = . Найти пересечение множеств.
Пересечением множеств М и К: М ⋂ К = Ø.
2. Объединение множеств (сложение) – это новое множество, которое состоит из всех элементов входящих в данные множества (А, В, С, D . ) , но повторяющиеся элементы считают только один раз. Если дано два множества А и В, а новое множество С, то С = А ∪ В или С = А + В ↔ С = В ∪ А или С = В + А. Изображение пересечения на рисунке 2.
Рис. 2. Объединение множеств А и В
Пример, даны два слова. А множество всех букв слова «компьютер» и В множество всех букв слова «монитор». Найти число букв в объединении множеств А и В.
Объединение множеств А и В: А ∪ В =
Пример из математики: Даны множества М = и К = . Найти объединение множеств.
Объединением множеств М и К: М ∪ К =
3. Дополнение множества В – это новое множество, которое состоит из всех элементов универсального множества А, кроме элементов множества В. Обозначается = А / В. Изображение дополнения на рисунке 3.
Рис. 3. Дополнение множеств А и В
Пример, дано множество М = и множество натуральных чисел N . Найти дополнение множества М относительно N .
Дополнением множества М: = N / М =
4. Разность множеств А и В – это новое множество, в котором есть элементы первоначального множества А, но нет элементов второго множества В. Обозначается А / В, но А / В ≠ В / А. Изображение разности на рисунке 4.
Пример, даны множества М = и К = . Найти разность множеств.
Разность множеств М и К: М / К =
Разность множеств К и М: К / М = .
Рис. 4. Разность множеств А и В
Рассмотрено четыре основных действий над множествами, которые будут необходимы для раздела практического применения. [3]
1.3 Диаграмма Эйлера-Венна
Диаграммы Эйлера и Венна применяются при решении задач для наглядного представления о множествах и действиях над ними. В данную диаграмму объединены круги Эйлера и диаграмма Венна (рис.5). Для начала расскажем об авторах данных диаграмм, а затем разберемся, в чем же эти круги одинаковы и в чем их различие.
Рис. 5. Леонард Эйлер и Джон Венн
Леонард Эйлер (1707-1783) математик, механик, физик, астроном, внесший большой вклад в развитие мировой науки. Эйлер впервые собрал в единую систему алгебру, анализ, тригонометрию, теорию чисел и другие дисциплины, а также сделал собственные открытия. Он написал более 850 работ по различным отраслям.
Джон Венн (1834-1923) английский математик и логик, известный как изложивший графический метод решения логических задач и расширивший математическую логику Джорджа Буля. Джон Венн является автором книги «Символическая логика», изданная в Лондоне в 1881г.
Диаграммы Венна и Эйлера очень схожи, так как основаны на теории множеств. Если же внимательно изучить данные диаграмм, то можно найти различие между ними. Это различие очень тонкое, делающее диаграммы уникальными. Диаграмма Венна показывает различные логические взаимоотношения между множествами, а диаграмма Эйлера также показывает эти взаимоотношения, но только те которые существуют в реальной действительности. Приведем пример для такого различия.
Пример 1. Подмножеством трех видов растений возьмём водоросли, мхи и папоротники (таблица 1). Найди комбинации пересечений.
Таблица 1. Виды растений
Задачу решим с помощью диаграммы Венна (рис.6а) и диаграммы Эйлера (рис.6в).
Из данных диаграмм видно, что круги в диаграмме Эйлера не пересекаются, так как данная диаграмма показывает только допустимые в реальной действительности комбинации, т.е. папоротники не могут быть мхами, а мха не может быть водорослью.
Рис. 6а. ДиаграммаДжона Венна
Рис. 6в. Диаграмма Леонард Эйлер
По высказыванию Джона Венна любые комбинации, даже если они не могут существовать в реальном мире, но в диаграмме Венна круги пересекаются. Поэтому некоторые задачи, решенные диаграммой Венна, переводят на диаграмму Эйлера.
Рассмотрим другой пример с колодой карт.
Пример 2. Дана колода карт. Необходимо составить композицию из подмножеств: красных карт, черных карт и крести.
Диаграмма Венна Диаграмма Эйлера
Рис. 7. Различие диаграмм Эйлер и Венна
Из этих диаграмм видна разница между всеми возможными и реальными комбинациями (рис.8). Круги в диаграмме Эйлера не пересекаются, так как черные и красные карты не имеют общих характеристик, а карты крести входят как подмножество в колоду черных карт. В диаграмме же Венна круги с черными, красными и крести колодами представляют четыре пересечения, но не имеют связи с реальностью. На этом примере также убеждаемся в разнице между диаграммами Эйлера и Венна. [4]
Делаем вывод: диаграмма Эйлера и диаграмма Венна по своей структуре похожи, но более достоверную, правильную информацию получаем из диаграммы Эйлера, так как она связывает различные задачи на понимание и применение окружающей нас действительности и реальной жизни.
Теория по понятию множества, действий над множествами, диаграмма Эйлера-Венна разобраны. Перейдем к практической части и решим несколько задач на множества с помощью диаграмм Эйлера-Венна.
2. Решение практических задач
Для решения практических задач на множества рассмотрим решение пяти задач с применением в математике и связанные с различной сферой деятельности.
Задача 1. Провели опрос среди 45 учеников: какой их любимый предмет? 16 учащихся ответили английский, 12 — математика и 17 — литература. Количество учеников увлекающихся: английским и литературой — 5, математикой и литературой — 4, математикой и английским — 3, и те кто увлекаются всеми предметами — 2. Для решения используйте диаграмму Эйлера-Венна, ответьте на следующие вопросы, записав ответ в виде процента:
а) сколько учеников предпочитают предметы английский язык и математику;
б) нравится только математика из количества учеников предпочитающих математику вместе с английским языком;
в) нравится только английский язык из количества учеников предпочитающих и английский язык и литературу;
г) нравится математика и литература;
д) не нравится математика, но увлекается литературой и английским;
Составим диаграмму Эйлера-Венна. Возьмём 3 пересекающихся круга, так как всего выбранных предметов 3 – математика, английский язык, литература и количество учеников выбравших 1, 2, 3 предмета разное. Ниже на рисунке 8 приведена диаграмма.
Рис. 8. Диаграмма выбор а предмета
а) используя данные построенной диаграммы найдем сколько учеников предпочитают предметы английский язык и математику, т.е. английский язык и математику выбирают 3 ученика, а всего учеников 45.
Значит отношение 3 : 45 = 6,67%
б) нравится только математика из количества учеников предпочитающих математику вместе с английским языком, найдем как отношение 3 : 3 = 100%.
в) нравится только английский язык из количества учеников предпочитающих и английский язык и литературу, найдем как отношение 6 : 26 = 23,07%
г) нравится математика и литература, найдем как отношение 4 : 45 = 8,89%
д) не нравится математика, но предпочитает литературу и английский язык, найдем как отношение 5 : 45 = 11,11%
Задача 2. Определить закрашенную область диаграмм (рис.9 a , 9 b , 9 c , 9 d ) :
Рис. 9а. А / (В ∪ С) ∪ (В ∩ С) Рис. 9в. А / (В ∪ С) ∪ В / (А ∪ С) ∪ (В ∩ С)
Рис. 9с. ( A ∩ B ∩ C ∩ D ) ∪ (( A ∩ C )/( D ∪ B )) ∪ (( D ∩ C )/( B ∪ A )) ∪ (( B ∩ D )/( A ∪ C )) ∩ (( A ∩ B )/( D ∪ C ))
Рис.9 d . B /( A ∪ C ∪ D ) ∪ D /( A ∪ C ∪ B ) ∪ (( A ∩ B ∩ C )/ D ) ∪ (( D ∩ B ∩ C )/ A ) ∪ (( A ∩ D ∩ C )/ B ) ∪ (( A ∩ B ∩ D )/ C )
Задача 3. Из 100 человек 37 используют Whatsapp, 44 — Вконтакте , 29 — Instagram, и 35 Facebook. В Whatsapp и Вконтакте зарегистрированы 4 человека, в Whatsapp и Instagram 6, в Whatsapp и Facebook 5, в Вконтакте и Facebook 7, в Вконтакте и Instagram 3, в Instagram и Facebook 5, в Whatsapp- Вконтакте- Instagram 3, Instagram- Вконтакте- Facebook 4, Facebook-Whatsapp-Instagram 6, Whatsapp- Вконтакте- Facebook 5 и 2 человека зарегистрированы во всех соц сетях. Какое количество людей не зарегистрированы в предложенных соц сетях?
Определим количество человек, которые пользуются только Whatsapp, только Вконтакт , только Instagram, только Facebook:
1) Whatsapp — 37 чел.,
Whatsapp и Вконтакт — 4 чел.,
Whatsapp и Instagram — 6 чел.,
Whatsapp и Facebook — 5 чел.,
Whatsapp- Вконтакте- Instagram — 3 чел.,
Facebook-Whatsapp-Instagram — 6 чел.,
Whatsapp- Вконтакте- Facebook — 5 чел.,
Во всех соц сетях 2 чел.
Значит, 37 – 4 – 6 – 5 – 3 – 6 – 5 – 2 = 6 чел. только Whatsapp
2) Вконтакт — 44 чел.,
Whatsapp и Вконтакте — 4 чел.,
Вконтакте и Facebook — 7 чел.,
Вконтакте и Instagram – 3 чел.,
Whatsapp- Вконтакте- Instagram — 3 чел.,
Instagram- Вконтакте- Facebook — 4 чел.,
Whatsapp- Вконтакте- Facebook — 5 чел.,
Во всех соц сетях 2 чел.
Значит, 44 – 4 – 7 – 3 – 3 – 4 – 5 – 2 = 16 чел. только Вконтакте
3) Instagram — 29 чел.,
Whatsapp и Instagram — 6 чел.,
Вконтакте и Instagram — 3 чел.,
Instagram и Facebook — 5 чел.,
Whatsapp- Вконтакте- Instagram — 3 чел.,
Instagram- Вконтакте- Facebook — 4 чел.,
Facebook-Whatsapp-Instagram — 6 чел.,
Во всех соц сетях 2 чел.
Значит, 29 – 6 – 3 – 5 – 3 – 4 – 6 – 2 = 0 чел. только Instagram
4) Facebook — 35 чел.,
Whatsapp и Facebook — 5 чел.,
Вконтакте и Facebook — 7 чел.,
Instagram и Facebook — 5 чел.,
Instagram- Вконтакте- Facebook — 4 чел.,
Facebook-Whatsapp-Instagram — 6 чел.,
Whatsapp- Вконтакте- Facebook — 5 чел.,
Во всех соц сетях 2 чел.
Значит, 35 – 5 – 7 – 5 – 4 – 6 – 5 – 2 = 1 чел. только Facebook
Найдём количество людей не зарегистрированных в предложенных соц сетях:
Общее количество человек 100
только Whatsapp — 6 чел.,
только Вконтакте — 16 чел.,
только Instagram — 0 чел.,
только Facebook — 1 чел.,
Whatsapp и Вконтакте — 4 чел.,
Whatsapp и Instagram — 6 чел.,
Whatsapp и Facebook — 5 чел.,
Вконтакте и Facebook — 7 чел.,
Вконтакте и Instagram – 3 чел.,
Instagram и Facebook – 5 чел.,
Whatsapp- Вконтакте- Instagram – 3 чел.,
Instagram- Вконтакте- Facebook — 4 чел.,
Facebook-Whatsapp-Instagram – 6 чел.,
Whatsapp- Вконтакте- Facebook – 5 чел.,
Во всех соц сетях 2 чел.
Значит, 100 — (6 + 16 + 0 + 1 + 4 + 6 + 5 + 7 + 3 + 5 + 3 + 4 + 6 +5 +2) = 27 чел.
Ответ: 27 человек не зарегистрированы в предложенных соц сетях
При решении этой задачи с помощью диаграммы Эйлера-Венна успрощается процесс вычисления. Зарисуем диаграмму и внесем все данные по этой задаче на рисунке 10.
Рис. 10. Диаграмма р егистр ации в различных соцсетях
100 – 73 = 27 чел.
Ответ: 27 человек не зарегистрированы в предложенных соц сетях
Задача 4. В Казахстане самые популярные книги казахских писателей:
1) Баян Мақсатқызы «Баян. Обо мне и не только» — 193 631 читатель,
2) Ермек Турсунов «Мелочи жизни» — 156 963 читателя.
Самые популярные книги зарубежных авторов:
3) Михаил Лабковский «Хочу и буду: Принять себя, полюбить жизнь и стать счастливым» — 185 757 читателей,
4) Джоан Роулинг «Гарри Поттер и Проклятое дитя. Части первая и вторая» — 177 419 читателей.
По рейтингу первую книгу прочитали 193 631 человек, вторую — 185 757 человек, третью — 177 419 человек, четвертую — 156 963 человека. Всего прочитано — 714 802 раза.
Количество людей, которые прочитали:
— первую и вторую книгу 31 382 читателя,
— первую и третью – 32 596 читателей,
— первую и четвертую – 19 848 читателя,
— вторую и третью — 21 821 читатель,
— вторую и четвертую – 12 130 читателей,
— третью и четвертую – 21 364 читателя,
— первую, вторую и третью – 34 828 читателя,
— первую, вторую и четвертую – 12 643 читателя,
— вторую, третью и четвертую – 31 543 читателя,
— первую, третью и четвертую – 23 456 читателей,
— все книги – 7 543 читателя.
a ) Сколько процентов составляет людей, которые прочитали первую и третью книгу от тех, кто читал только вторую книгу?
b ) Сколько процентов составляет людей, прочитавших только одну книгу от тех кто прочитал две книги?
c ) Какая самая популярная книга?
d ) Сколько процентов составляет людей, которые прочитали только одну книгу; две книги; три книги и четыре книги?
Для решения данного задания построим диаграмму Эйлера-Венна и найдем количество читателей, которые прочитали только одну книгу (рис.11).
Из диаграммы видно, что первую книгу прочитали 31 335 читателей, вторую — 33 867 читателей, третью – 4 268 читателей, четвертую – 28 436 читателя.
Рис. 11. Диаграмма популярны х книг в Казахстане
Теперь можно ответить на вопросы данной задачи:
a ) первую и третью книгу прочитали 32 596 читателя, а только вторую книгу — 33 867 читателей. Значит, это соотношение равно:
b ) Найдем количество людей, которые прочитали две книги и людей, которые прочитали только одну книгу.
31 382 + 32 596 +19 848 + 21 821 + 12 130 + 21 364 = 139 141 читатель
31 335 + 33 867 + 4 268 + 28 436 = 97 906 читателей
Значит, это соотношение равно:
c ) Баян Мақсатқызы «Баян. Обо мне и не только» — 193 631 читателей
d ) Количество человек участвовавших в опросе:
31 335 + 31 382 + 33 867 + 4 268 + 32 596 + 34 828 + 21 821 + 21 364 + 23 456 +
7 543 + 31 543 + 28 436 + 19 848 + 12 643 + 12 130 = 347060 человек
прочитали только одну книгу:
Задача 5. На диаграмме показано, сколько человек имеют брендовые сотовые телефоны X iaomi, Samsung, H uawei, I phone. (рис 12)
1) Буквы можно заменить числами, решив следующие задания:
А. Найди дискриминант уравнения: 5х² + 60х – 14,9 = 0
В. Вычисли: 85 · , при n = 6
D . Найди произведение корней уравнения: (х – 23)·(х – 67)·(х – 2) = 0
F . Найди следующее число в последовательности: 479; 958; 1916;
2) Определи, к какому множеству относится данные бренды телефонов, если известно, что:
a ) найди количество людей, которые имеют все четыре вида телефона на 1203 меньше чем те, которые имеют только два вида телефона H uawei и I phone;
b ) найди количество людей, которые имеют три вида телефона I phone, X iaomi, H uawei на 427 больше чем те, которые имеют три иные вида телефона X iaomi, I phone, Samsung.
Рис. 12. Количество брендовых сотовых телефонов
Решение Найдем значения букв для дальнейшего использования диаграммы (рис. 12а)
Рис. 12 а . Количество брендовых сотовых телефонов с дополнениями
А. Найди дискриминант уравнения:
5х² + 60х – 14,9 = 0
D = 60² — 4 · 5 · (-14,9) = 3 898
В. Вычисли: 85 · , при n = 6
D . Найди произведение корней уравнения:
(х – 23)·(х – 67)·(х – 2) = 0
23 · 67 · 2 = 3 082
F . Найди следующее число в последовательности: 479; 958; 1916;
3 000 – 9 · 11 = 2901
1) А. 3898; В. 5440; С. 4942; D . 3082; F . 3832; G . 2901.
a ) количество людей, которые имеют все четыре вида телефона – 1698, те, кто имеют только два вида телефона H uawei и I phone – 2901. Значит, можно определить два множества с телефонами H uawei и I phone, но точно указать какое множество пока невозможно;
b ) количество людей, которые имеют три вида телефона I phone, X iaomi, H uawei – 5079, те, которые имеют три иные вида телефона X iaomi, I phone, Samsung — 4652. Отсюда видно, что X iaomi и I phone повторяются дважды, а Samsung и H uawei один раз.
Значит, принимая во внимание а) и b ) можно определить порядок слева на право: Samsung, X iaomi, H uawei, I phone (рис. 12в).
Рис. 12в. Брендовые сотовые телефоны
В практической части разобраны пять различных авторских задач на множество. С помощью диаграмм Эйлера-Венна даны подробные, наглядные решения задач.
3. Диаграмма Эйлера-Венна в исследовании
Исследование проведено среди учащихся 7-9 классов. В исследовании участвовали 155 учеников. Анкета состоит из 7 различных вопросов (приложение 1). Разберем каждый вопрос в отдельности и сделаем выводы.
1 вопрос: Какой напиток пьете по утрам?
Ответы: только чай пьют 63 ученика, только кофе – 36, и чай, и кофе – 53, другое – 21. Если сложить эти числа, то получим:
63 + 36 + 53 + 21 = 173 ученика
Значит, некоторые ученики ответили на вопрос анкеты, выбрав два или более ответа. В дополнительных сведениях можно найти, кто сделал более одного выбора в ответах.
«и чай, и кофе» и «только чай» — 1 ученик,
«и чай, и кофе» и «другое» — 4 ученика,
«и чай, и кофе», «только чай», «только кофе» — 3 ученика,
«и чай, и кофе» и «только кофе» — 2 ученика,
«только чай» и «другое» — 5 ученик.
Определим, какой больше всего напиток предпочитают учащиеся. Для этого построим диаграмму Эйлера-Венна (рис. 13) .
Рис. 13. Диаграмма выбора напитка
Из этой диаграммы видно, что учащиеся больше всего предпочитают напиток «чай», что составляет 112 учеников или 72%. [5]
2 вопрос: Каким видом спорта занимаешься?
Ответы: футбол — 14 ученика, плавание – 20, шахматы – 18, другое – 119. Сложим числа и получим:
14 + 20 + 18 + 119 = 171 ученик
В дополнительных сведениях:
«футбол» и «шахматы» — 2 ученика,
«футбол» и «плавание» — 1 ученик,
«плавание», «другой вид спорта» — 4 ученика,
«футбол», «другой вид спорта» — 2 ученика,
«шахматы», «другой вид спорта» — 5 учеников,
«шахматы», «футбол», «другой вид спорта» — 1 ученик.
Определим, сколько учеников не занимается спортом. Для этого построим диаграмму Эйлера-Венна (рис. 14) .
Рис. 14. Диаграмма по увлечению спорта
Вычислим, сколько учащихся не занимается спортом:
155 – (10 + 15 + 8 + 67 + 1 + 2 + 4 + 5 + 1 + 2) = 40 учеников или 26%.
3 вопрос: Какие языки знаешь в совершенстве?
Ответы: Казахский язык – 95 учеников, русский язык – 138 учеников, английский язык — 46 ученик, другие языки – 2 ученика. Сложим числа и получим:
95 + 138 + 46 + 2 = 281 ученик.
Определим, наибольшее количество учащихся, которые в совершенстве знают два языка (рис. 15).
Рис. 15. Диаграмма знания языка
В дополнительных сведениях:
«казахский» и «русский» — 54 ученика,
«казахский» и «английский» — 1 ученик,
«русский» и «английский» — 5 ученика,
«казахский», «русский» и «английский» — 30 ученика,
«казахский», «русский», «английский» и «другое» — 2 ученика
Определим количество учеников, которые владеют двумя языками:
казахский и русский язык:
54 + 30 + 2 = 86 учеников
казахский и английский язык:
30 + 2 +1 = 33 ученика
русский и английский язык:
30 + 5 + 2 = 37 учеников
Значит, 86 учеников в совершенстве владеют казахским и русским языком.
5 вопрос: Каков Ваш любимый цвет?
Ответы: Зеленый цвет – 23 ученика, синий цвет – 26 учеников, красный цвет — 29 учеников, другие цвета – 116 учеников. Сложим числа и получим:
23 + 26 + 29 + 116 = 194 ученика.
Сравним, процент учащихся, которые выбрали только один цвет с теми, кто выбрал два и более цвета (рис. 16).
Рис. 16. Диаграмма выбор а цвета
В дополнительных сведениях:
«зеленый» и «синий» — 1 ученик,
«зеленый» и «красный» — 1 ученик,
«зеленый» и «другой» — 4 ученика,
«зеленый», «красный» и «другой» — 1 ученик,
«зеленый», «синий» и «красный» — 1 ученик,
«зеленый», «синий», «красный» и «другой» — 2 ученика,
«зеленый», «синий» и «другой» — 3 ученика,
«синий» и «красный» — 3 ученика,
«синий», «красный», «другой» — 2 ученика,
«синий» и «другой» — 3 ученика,
«красный» и «другой» — 7 ученика.
Учащиеся, которые выбрали только один цвет:
10 + 11 + 12 + 94 = 127 ученик
выбрали два и более цвета:
1 + 3 + 7 + 1 + 2 + 1 + 2 + 3 + 1 + 3 + 4 = 28 учеников
Сравним, процент учащихся, которые выбрали только один цвет с теми, кто выбрал два и более цвета:
Значит, процент учащихся, которые выбрали только один цвет больше на 64% (99 ученика), чем учащихся, выбравших два и более цвета.
6 вопрос: Где проводишь летние каникулы?
Ответы: В своем городе – 121 ученик, в деревне – 36 учеников, в другом городе Казахстана — 19 учеников, за пределами Казахстана – 57 учеников. Сложим числа и получим:
95 + 138 + 46 + 2 = 281 ученик.
Сравним, количество учащихся, которые отдыхают на летних каникулах в разных местах (рис. 17).
Рис. 17. Диаграмма проведения летних каникул
В дополнительных сведениях:
«в деревне» и «в своем городе» — 13 учеников,
«в деревне» и «другой город Казахстана» — 3 учеников,
«другой город Казахстана» и «в своем городе» — 20 ученика,
«другой город Казахстана» и «за пределами Казахстана» — 3 ученика,
«в деревне», «за пределами Казахстана» и «в своем городе» — 1 ученик,
«в своем городе», «за пределами Казахстана» и «другой город Казахстана» — 8 учеников,
«в деревне», «за пределами Казахстана» и «другой город Казахстана» — 3 ученика,
«в деревне», «в своем городе» и «за пределами Казахстана» — 9 ученика.
Количество учащихся, которые проводят летние каникулы только в одном месте:
8 + 69 + 3 + 16 = 96 учеников
14 + 17 + 3 + 3 + 3 = 40 учеников
1 + 8 + 9 + 1 = 19 учеников
Если сравнить полученные данные, то видно, что летние каникулы ребята проводят в основном в одном месте – 62%, в двух местах проводят – четверть учащихся, в трех местах самое меньшее количество учащихся – 12%.
Из данного исследования, следует, что в вопросах 1, 2, 3, 5, 6, проведен анализ ответов учащихся, дан ответ на поставленный актуальный вопрос и показана диаграмма Эйлера-Венна. На 4 и 7 вопрос учащиеся ответили только одним ответом, поэтому пересечения кругов Эйлера-Венна нет.
Первый вопрос актуален для организаций общественного питания, можно предложить для кафе, ресторанов при составлении меню, выяснить не только кофе или чай предпочитают посетители, но и какую еду больше употребляют жители.
Второй вопрос о спорте, необходим при выборе открытия или проведения той или иной секции в комплексах, регионах, областях и т.д. Третий вопрос можно использовать при открытии каких-либо языковых центров и т.д. Эти два вопроса переплетаются.
Пятый вопрос актуален в психологии, где можно применить круги Эйлера-Венна при определении характера, темперамента и других качеств человека.
Шестой вопрос как проводить каникулы школьникам можно порекомендовать школам, колледжа, институтам. Чтобы организовать путевки в различные места, так как ученики в основном находятся в своем городе и редко посещает новые. Если школьники будут посещать различные лагеря отдыха, курорты и путешествовать, то у учеников повыситься интерес к изучению увлекательных и познавательных мест планеты.
Вывод: применение диаграммы Эйлера-Венна расширяет спектр данных, по сравнение с графиками и различными диаграммами.
Для наглядности предоставляю макет диаграммы Эйлера-Венна, состоящий из 3 множеств (рис.18).
Рис. 1 8 . Макет диаграмма Эйлера-Венна
Макет изготовлен на 3 D принтере, где видно как пересекаются множества друг с другом в 3 D пространстве.
В математике используют различные понятия, такие как числа, функция, геометрические фигуры и т.д. Все это является множеством. Множество это фундамент математики. Множество представляет какое-то количество предметов, объектов, но кроме этого множеством обозначают и объекты, состоящие из одного или вообще не имеющего количества предметов.
Данная работа состоит из трех частей: теоретической, практической и исследовательской.
В начале изучил теоретические аспекты множеств: историю множеств, понятие множества, из каких элементов может состоять множество, какие есть виды множеств (пустое, конечное, бесконечное, универсальное), какие действия можно осуществлять над множествами (п ересечение множеств (произведение), объединение множеств (сложение), д ополнение множества, разность множеств). Также при изучении теории множеств определил различие между кругами Эйлера и кругами Венна.
Изучение теории множеств привела к такой мысли: какие же задачи можно составить на множества с использаванием диаграммы Эйлера-Венна. При решении некоторых задач на множество удобно применять диаграмму Эйлера-Венна, в особенности задачи имеющее большие по объему решения. Диаграмма наглядно представляет все действия над множеством. В практической части разобраны авторские задачи, которые решаются с помощью диаграмм Эйлера-Венна. В решении задач применяются диаграммы не только состоящие из 3 кругов, но и из 4 кругов.
Проведено анкетирование для исследовательской работы. Вопросы анкеты составлены для учащихся 7-9 классов. Анализ ответов 155 учеников изображался на диаграммах Эйлера-Венна, где можно было видеть развернутое представление об ответах учащихся. По данным диаграммам можно видеть сколько выборов сделали ученики, отвечая на вопросы, что интересует их больше всего или сколько учащихся ни чем не заинтересованы. Подводя итоги исследовательской работы предоставлены выводы по каждому вопросу и показаны применения диаграммы Эйлера-Венна в различных сферах деятельности.
Изготовлен макет на 3 D принтере для наглядного представления понятия множества.
Вывод: решение задач на множества с помощью диаграмм Эйлера-Венна сокращает ход решения, а наглядность диаграммы дает более быстрый ответ на вопрос задачи по сравнению со стандартным решением.
Список использованной литературы
1. Электронная еврейская энциклопедия, 1988. Том 4, с.80
2. Н.Я.Виленкин Рассказы о множествах. 3-е издание. – М.: МЦНМО , 2005, с.150 https://clck.ru/RwWog
3. С.А.Ануфриенко Введение в теорию множеств и комбинаторику. Учебное пособие. – Екатеринбург: УрГУ, 1998, с.62
4. Статья «Диаграммы Эйлера против диаграммы Венна» https :// creately . com / blog /
5. Джим Вуланд , Математика 2 издание. Часть 1, модуль 3. 14с.
6. Верещагин Н.К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. – 5-у изд., — М.: МЦНМО, 2017. -112 с.
7. Mathprofi http :// mathprofi . ru / mnozhestva . html
8. Киреенко С.Г., Гриншпон И.Э Элементы теории множеств. Учебное пособие. — Томск, 2003. – 42с
9. Шахмейстер А.Х. «Множества. Функции. Последовательности. Прогрессии» — М.: МЦНМО, 2014. — 296 с.
10. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — 3-е изд. — М.: Физматлит, 1995. — 256 с.
11. Александров П. С. Введение в теорию множеств и общую топологию. — М.: Наука, 1977. 368 с
Результаты анкетирования среди учащихся 7-9 классы
Видео:Пересечение и объединение множеств.Решение примеровСкачать

Круги Эйлера — примеры и методы решения логических задач
Видео:Круги Эйлера (диаграммы Венна) - просто и доступно.Скачать

Множества в математике
Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:
- конечное, например, множество стран;
- бесконечное — множество звёзд во вселенной;
- пустое — множество острых углов в прямоугольнике.
Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.
В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:
- дополнение ¯A в калькуляторе имеет вид A’;
- пересечение A∩B представлено как A intersection B;
- объединение А⋃B обозначено A union B;
- симметрическая разность A∆B — symmetric difference of A and B;
- Относительное дополнение AB — AB.
Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.
Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.
Видео:Множества. Операции над множествами. 10 класс алгебраСкачать

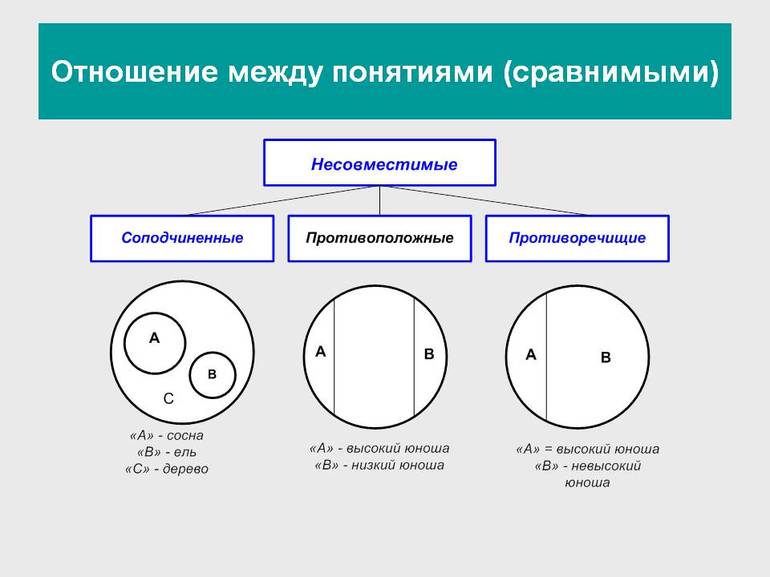
Отношения между понятиями
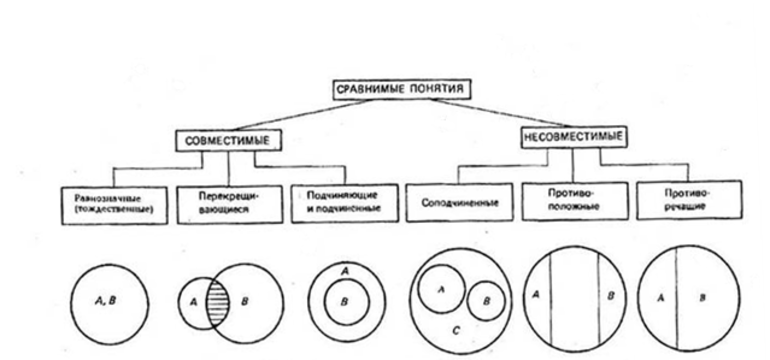
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.
Рисунок 1
Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:
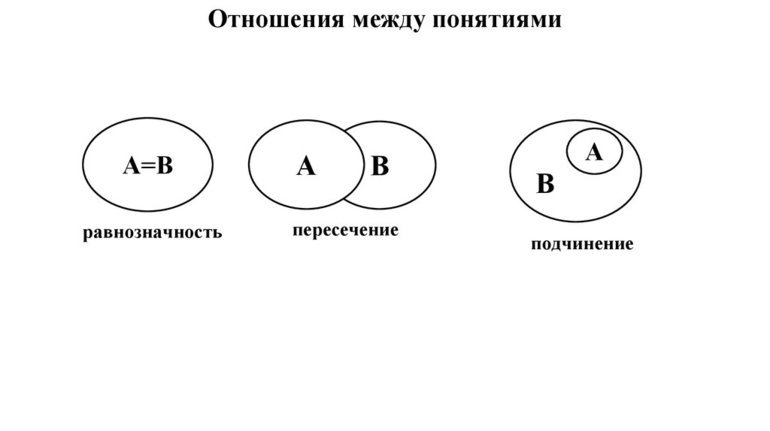
- равнозначные (тождественные);
- перекрещивающиеся;
- подчиняющие и подчинённые.
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).
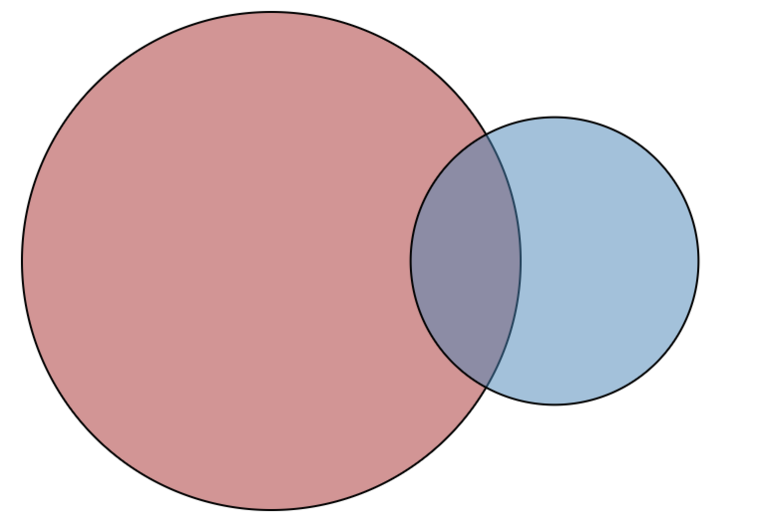
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.
Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».
Несовместимыми называют понятия, не имеющие общих элементов:
- соподчинённые;
- противоположные;
- противоречащие.
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.
Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).
Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.
Видео:Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебраСкачать

Решение задач, примеры
Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.
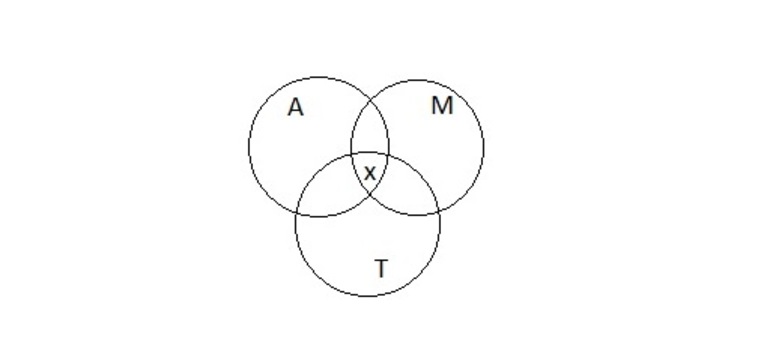
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?
Рисунок 2
Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.
Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…
Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…
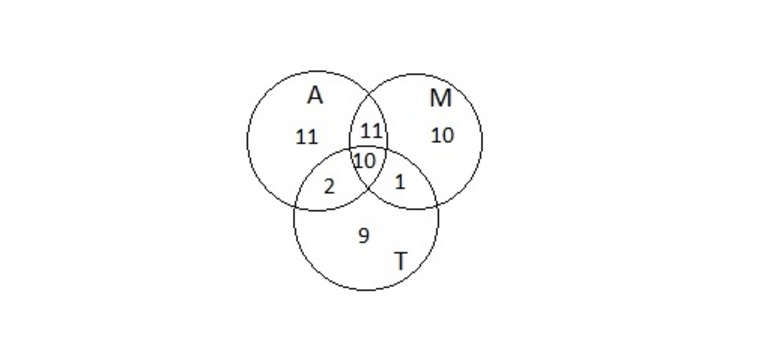
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.
Рисунок 3
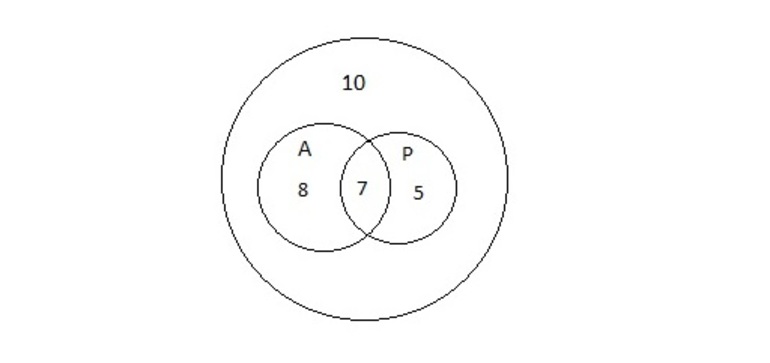
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.
Рисунок 4
Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.
🌟 Видео
Диаграммы Эйлера - Венна (задача)Скачать

Множества и круги Эйлера для 8 задания на ОГЭ по информатике 2024 | УмскулСкачать

Множества. Круги ЭйлераСкачать

Множества. Круги Эйлера. Математика 5, 6, 7, 8, 9, 10, 11 класс. Подготовка к ЕГЭ, ОГЭ, ЦТ, экзаменуСкачать

Операции над множествамиСкачать

Введение в теорию вероятности. Диаграмма Венна.Скачать