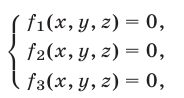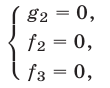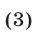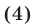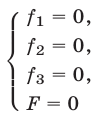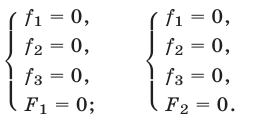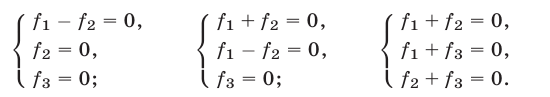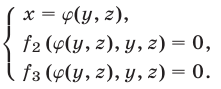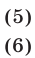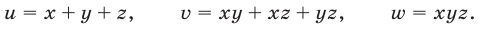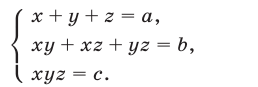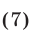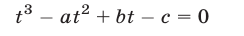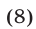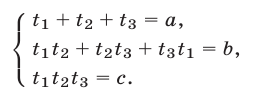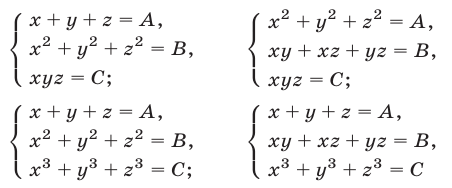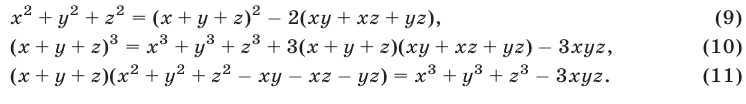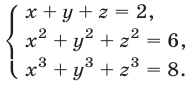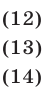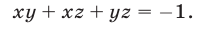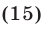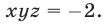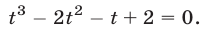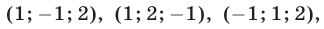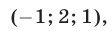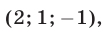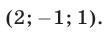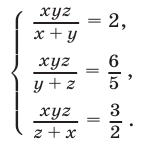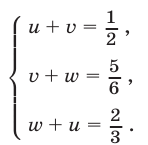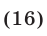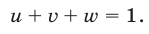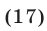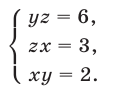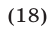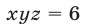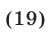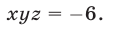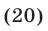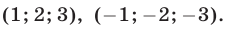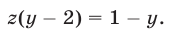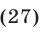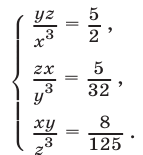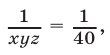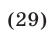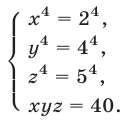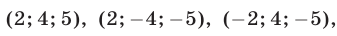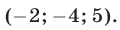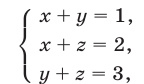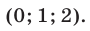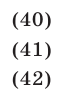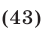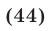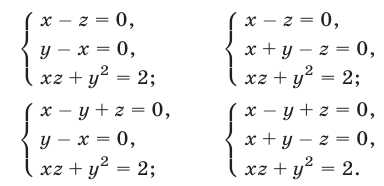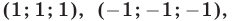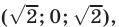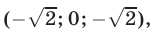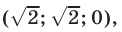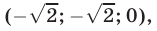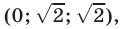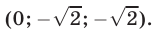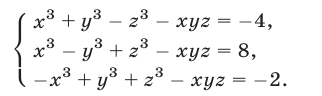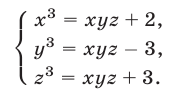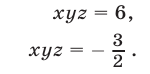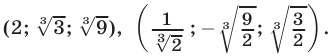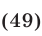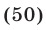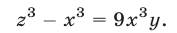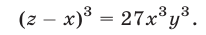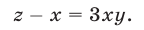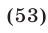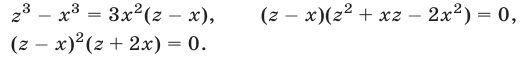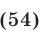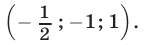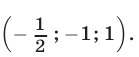Решить уравнение с тремя иксами

62. Одно уравнение с тремя неизвестными . Пусть имеем уравнение

На это уравнение можно смотреть, как на запись задачи: найти числовые значения для x, y и z, чтобы трехчлен 3x + 4y – 2z оказался равен числу 11. Таким образом это уравнение является уравнением с тремя неизвестными. Так как мы можем решить одно уравнение с одним неизвестным, то уже с первого взгляда возникает мысль, что 2 неизвестных здесь являются как бы лишними, и им можно давать произвольные значения. И действительно, если, например, взять для y число 3 и для z число 5, то получим уравнение с одним неизвестным:

Возьмем другие числа для y и z. Например, пусть

Тогда получим уравнение:

Продолжая эту работу дальше, мы придем к заключению:

Одно уравнение с тремя неизвестными имеет бесконечно много решений, и для получения их надо двум неизвестным давать произвольные значения.

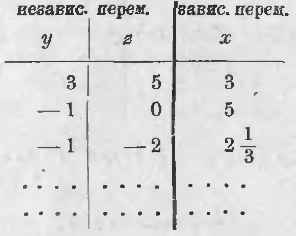
Результаты этой работы можно записать в таблице (мы, кроме двух уже найденных решений, записали в ней еще одно, которое получится, если положить y = –1 и z = –2):

Так как для y и для z мы берем произвольные значения, то они являются независимыми переменными, а x является зависимым (от них) переменным. Другими словами: x является функциею от y и z.

Чтобы удобнее получать решения этого уравнения, можно определить из него x через y и z. Получим:

3x + 4y – 2z = 11; 3x = 11 – 4y + 2z;
x = (11 – 4y + 2z) / 3.

Дадим, напр., значения: y = 5 и z = 1; получим: x = (11 – 20 + 2) / 3 = –2(1/3) и т. д.

Возьмем еще уравнение

Примем x и y за независимые переменные, а z — за зависимое и определим z через x и y

–2z = 7 – 3x + 5y; 2z = 3x – 5y – 7; z = (3x – 5y – 7) / 2

Видео:Как решать уравнения с дробью? #shortsСкачать

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$

Определим главный определитель системы:

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$

и вспомогательные определители :

$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end — b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$

$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac = 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$

$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin -2 & 3 \ 9 & -1 \ end — 1 = begin -2 & -1 \ 9 & 2 \ end = $$

$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end — 13 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -2 \ 1 & 9 \ end = $$

$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end — 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$

$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end — 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$

$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end — 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Алгебраические системы с тремя неизвестными с примерами решения

Алгебраические системы с тремя неизвестными

Для систем с тремя неизвестными определения понятий равносильности и следствия, а также свойства преобразований систем формулируются аналогично тому, как это было сделано для систем с двумя неизвестными.

Будем рассматривать системы вида

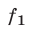
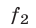
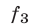
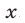
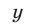
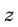
где , , являются либо многочленами от , , , либо могут быть представлены в виде отношения многочленов.

Сформулируем для систем уравнений с тремя неизвестными следующие утверждения, которые могут оказаться полезными при решении систем.

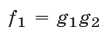
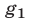
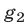
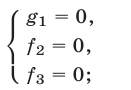
1° Если , где и —многочлены, то система (1) равносильна совокупности систем

и поэтому множество решений системы (1) в этом случае есть объединение множеств решений систем (2) и (3).

2°. Если уравнение

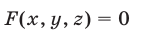
есть следствие системы (1), то система

равносильна системе (1), т. е. при добавлении к системе (1) еще одного уравнения (4), являющегося следствием этой системы, получается система, равносильная системе (1).

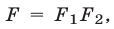
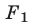
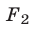
3°. Если уравнение (4) — следствие системы (1), причем где и —многочлены, то система (1) равносильна совокупности систем

4°. Система (1) равносильна каждой из следующих систем:

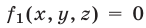
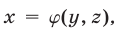
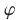
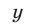
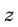
5°. Если уравнение равносильно уравнению где — многочлен от и , то система (1) равносильна системе

Это утверждение лежит в основе метода исключения неизвестных: система (1) сводится к системе (5), (6) с двумя неизвестными.

Прежде чем переходить к примерам алгебраических систем с тремя неизвестными, отметим, что нет общих рецептов для нахождения решений систем. Каждый раз нужно учитывать конкретные особенности рассматриваемой системы. Можно дать только общий совет: решайте побольше задач.

Рассмотрим сначала системы с тремя неизвестными, которые сводятся к кубическим уравнениям.

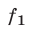
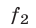
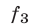
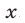
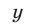
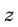
К таким системам относятся системы симметрических алгебраических уравнений, т.е. системы вида (1), где , , — многочлены, каждый из которых не меняется, если поменять местами любую пару из переменных , , .

В этом случае удобно ввести следующие переменные:

Простейший пример системы рассматриваемого вида — система

Система (7) и кубическое уравнение

связаны следующим образом.

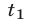
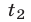
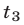
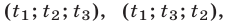
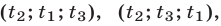
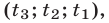
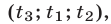
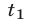
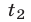
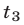
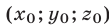
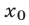
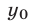
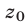
Если , , — корни уравнения (8), то система (7) имеет шесть решений: получаемых всевозможными перестановками трех чисел , , . Обратно, если решение системы (7), то , , — корни уравнения (8).

Доказательство этого утверждения основано на использовании формул Виета для корней уравнения (8):

Для сведения к системам (7) систем симметрических уравнений вида

можно использовать следующие тождества:

Примеры с решениями

Пример №186.

Решить систему уравнений

Решение:

Используя уравнения (12), (13) и тождество (9), получаем

Применяя формулу (11) и учитывая равенства (13)-(15), находим

Следовательно, исходная система равносильна системе вида (7), в которой 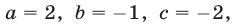, а уравнение (8) имеет вид

Корни этого уравнения — числа 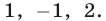Поэтому система имеет шесть решений, получаемых перестановкой чисел

Ответ.

Обратимся теперь к системам с тремя неизвестными, которые не являются симметрическими.

Пример №187.

Решить систему уравнений

Решение:

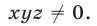
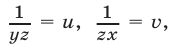
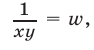
Так как правые части уравнений отличны от нуля, то Полагая получаем систему линейных уравнений

Сложив уравнения системы (16), находим

Из (16) и (17) получаем 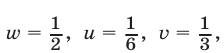т. е.

Перемножив почленно уравнения системы (18), которая равносильна исходной, имеем 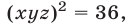откуда

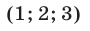
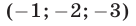
Следовательно, исходная система равносильна совокупности систем (18), (19) и (18), (20), которые имеют решения и соответственно.

Ответ.

Пример №188.

Решить систему уравнений

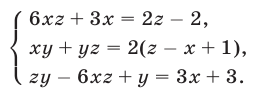
Решение:

Будем решать систему методом исключения неизвестных и сведением, в конечном счете, к одному уравнению с одним неизвестным. Складывая почленно уравнения (21) и (23), получаем

Так как 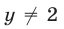на основании равенства (24), то из этого равенства следует, что

Запишем далее уравнение (22) в виде

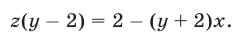
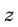
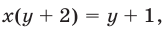
Исключив из уравнений (24) и (26), получаем откуда

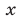
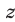
Заметим, что система (27), (25), (21) равносильна системе (21)— (23). Подставляя выражения для и из формул (27) и (25) в уравнение (21), получаем

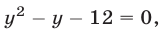
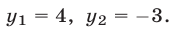
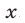
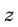
или откуда Соответствующие значения и найдем по формулам (27) и (25).

Ответ.

Пример №189.

Решить систему уравнений

Решение:

Перемножив уравнения системы (28), получаем

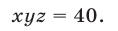
Уравнение (29) является следствием системы (28), которая равносильна системе

Уравнения (30), (31), (32) имеют решения 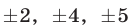соответственно. С учетом равенства (29) находим четыре решения системы (28).

Ответ.

Пример №190.

Найти решения системы уравнений

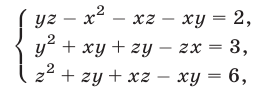
Решение:

Вычитая из уравнения (34) уравнение (33), получаем

Далее, вычитая из уравнения (35) уравнение (33), находим

Наконец, складывая уравнения (34) и (35), получаем

Система (37)-(39) равносильна системе (33)-(35), а при условии (36) — системе линейных уравнений

имеющей единственное решение

Ответ.

Пример №191.

Решить систему уравнений

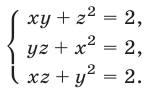
Решение:

Вычтем из уравнения (41) уравнение (40) и преобразуем полученное уравнение к виду

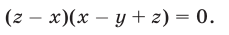
Выполнив ту же операцию с уравнениями (42) и (41), имеем

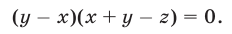
Система (43), (44), (42), равносильная системе (40)-(42), распадается на следующие четыре системы:

Полученные системы легко решаются методом исключения неизвестных. Объединив решения этих систем, найдем все решения исходной системы.

Ответ.

Пример №192.

Решить систему уравнений

Решение:

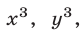
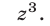
Решим эту систему как линейную относительно Для этого сложим попарно уравнения системы (45) и получим систему

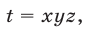
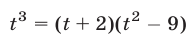
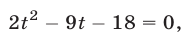
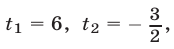
Перемножив уравнения системы (46) и полагая находим или откуда т. е.

Система (45) в силу утверждения 3° равносильна совокупности систем (46), (47) и (46), (48), каждая из которых имеет единственное решение.

Ответ.

Пример №193.

Решить систему уравнений

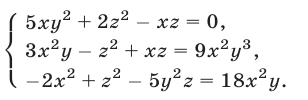
Решение:

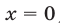
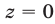
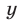
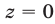
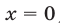
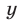
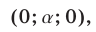
Если , то из системы (49) следует, что , а может принимать любые значения. Аналогично, если , то , — любое. Таким образом, система имеет бесконечное множество решений вида

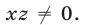
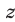
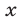
Будем искать решения системы (49) такие, что . Умножив первое уравнение системы (49) на , а третье — на и сложив результаты, получим

Прибавив к уравнению (51) второе уравнение системы (49), умноженное на 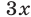:, находим

Каждое из уравнений (51), (52) является следствием системы (49).

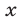
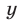
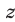
Так как , , — действительные числа (требуется найти действительные решения системы), то уравнение (52) равносильно уравнению

Исключая 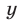из уравнений (53) и (51), получаем

Уравнения (53) и (54) являются следствиями системы (49), а уравнение (54) равносильно совокупности уравнений

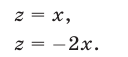
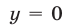
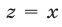
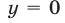
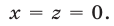
Из (55) и (53) следует, что , а из системы (49) при и находим Полученное решение содержится среди решений (50).

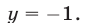
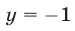
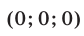
Из (56) и (53) следует, что Подставляя в систему (49), находим решения и

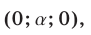
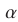
Ответ. — любое действительное число;

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🔥 Видео

Никто не решил ➜ Удобная подстановка ➜ Решите уравнение ➜ x^3-3x+1=0Скачать

ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Система с тремя переменнымиСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

Математика | Кубические уравнения по методу СталлонеСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Простые уравнения. Как решать простые уравнения?Скачать

Уравнение с X и Y #shortsСкачать

Решение матричных уравненийСкачать

КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Решите уравнение x^3+4x^2=9x+36. ОГЭ по математике. 2 часть. Номер 20.Скачать

Решение уравнения третьей степени x³-9x-12=0Скачать

Решите уравнение (-5x+3)(-x+6)=0. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Решение уравнения с модулем |x+8|+|x-3|+|x+2|=1.Скачать