Решить уравнение с помощью алгебраических дополнений (2 видео)

Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.

Содержание

Минор $M_$ элемента $a_$
Алгебраическое дополнение $A_$ элемента $a_$
Минор k-го порядка матрицы $A_$
Минор k-го порядка матрицы $A_$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.
Алгебраические дополнения
Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
Пример решения системы линейных уравнений с помощью метода обратной матрицы
🌟 Видео

Видео:Миноры и алгебраические дополненияСкачать

Минор $M_$ элемента $a_$

Пусть задана квадратная матрица $A_$ (т.е. квадратная матрица n-го порядка).

Для примера рассмотрим квадратную матрицу четвёртого порядка: $A=left( begin 1 & 0 & -3 & 9\ 2 & -7 & 11 & 5 \ -9 & 4 & 25 & 84\ 3 & 12 & -5 & 58 end right)$. Найдём минор элемента $a_$, т.е. найдём $M_$. Сперва запишем минор $M_$, а потом вычислим его значение. Для того, чтобы составить $M_$, вычеркнем из матрицы $A$ третью строку и второй столбец (именно на пересечении третьей строки и второго столбца расположен элемент $a_$). Мы получим новую матрицу, определитель которой и есть искомый минор $M_$:

Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$ M_=left| begin 1 & -3 & 9\ 2 & 11 & 5 \ 3 & -5 & 58 end right|= 1cdot 11cdot 58+(-3)cdot 5cdot 3+2cdot (-5)cdot 9-9cdot 11cdot 3-(-3)cdot 2cdot 58-5cdot (-5)cdot 1=579. $$

Итак, минор элемента $a_$ равен 579, т.е. $M_=579$.

Часто вместо словосочетания «минор элемента матрицы» в литературе встречается «минор элемента определителя». Суть остается неизменной: чтобы получить минор элемента $a_$ нужно вычеркнуть из исходного определителя i-ю строку и j-й столбец. Оставшиеся элементы записывают в новый определитель, который и является минором элемента $a_$. Например, найдём минор элемента $a_$ определителя $left| begin -1 & 3 & 2\ 9 & 0 & -5 \ 4 & -3 & 7 end right|$. Чтобы записать требуемый минор $M_$ нам понадобится вычеркнуть из заданного определителя первую строку и второй столбец:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:

$$ M_=left| begin 9 & -5\ 4 & 7 end right|=9cdot 7-(-5)cdot 4=83. $$

Итак, минор элемента $a_$ равен 83, т.е. $M_=83$.

Видео:Обратная матрица методом алгебраических дополненийСкачать

Алгебраическое дополнение $A_$ элемента $a_$

Пусть задана квадратная матрица $A_$ (т.е. квадратная матрица n-го порядка).

где $M_$ – минор элемента $a_$.

Найдем алгебраическое дополнение элемента $a_$ матрицы $A=left( begin 1 & 0 & -3 & 9\ 2 & -7 & 11 & 5 \ -9 & 4 & 25 & 84\ 3 & 12 & -5 & 58 end right)$, т.е. найдём $A_$. Ранее мы уже находили минор $M_=579$, поэтому используем полученный результат:

Обычно при нахождении алгебраических дополнений не вычисляют отдельно минор, а уж потом само дополнение. Запись минора опускают. Например, найдем $A_$, если $A=left( begin -5 & 10 & 2\ 6 & 9 & -4 \ 4 & -3 & 1 end right)$. Согласно формуле $A_=(-1)^cdot M_=-M_$. Однако чтобы получить $M_$ достаточно вычеркнуть первую строку и второй столбец матрицы $A$, так зачем же вводить лишнее обозначение для минора? Сразу запишем выражение для алгебраического дополнения $A_$:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Минор k-го порядка матрицы $A_$

Если в предыдущих двух пунктах мы говорили лишь о квадратных матрицах, то здесь поведём речь также и о прямоугольных матрицах, у которых количество строк вовсе не обязательно равняется количеству столбцов. Итак, пусть задана матрица $A_$, т.е. матрица, содержащая m строк и n столбцов.

Например, рассмотрим такую матрицу:

$$A=left( begin -1 & 0 & -3 & 9\ 2 & 7 & 14 & 6 \ 15 & -27 & 18 & 31\ 0 & 1 & 19 & 8\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end right) $$

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Напомню, что главными диагональными элементами именуют те элементы матрицы, у которых индексы равны: $a_$, $a_$, $a_$ и так далее. Например, для рассмотренной выше матрицы $A$ такими элементами будут $a_=-1$, $a_=7$, $a_=18$, $a_=8$. На рисунке они выделены зелёным цветом:

$$left( begin boldgreen & 0 & -3 & 9\ 2 & boldgreen & 14 & 6 \ 15 & -27 & boldgreen & 31\ 0 & 1 & 19 & boldgreen\ 0 & -12 & 20 & 14\ 5 & 3 & -21 & 9\ 23 & -10 & -5 & 58 end right) $$

Например, если в матрице $A$ мы вычеркнем строки и столбцы с номерами 1 и 3, то на их пересечении будут расположены элементы минора второго порядка, на главной диагонали которого будут находиться только диагональные элементы матрицы $A$ (элементы $a_=-1$ и $a_=18$ матрицы $A$). Следовательно, мы получим главный минор второго порядка:

$$ M=left|begin boldgreen & -3 \ 15 & boldgreen end right| $$

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

$$A=left( begin -1 & 0 & 3 & 0 & 0 \ 2 & 0 & 4 & 1 & 0\ 1 & 0 & -2 & -1 & 0\ 0 & 0 & 0 & 0 & 0 end right) $$

Запишем минор этой матрицы, элементы которого расположены на пересечении строк №1, №2, №3 и столбцов с №1, №3, №4. Мы получим минор третьего порядка (его элементы выделены в матрице $A$ фиолетовым цветом):

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

$$ M=left| begin -1 & 3 & 0\ 2 & 4 & 1 \ 1 & -2 & -1 end right|=4+3+6-2=11. $$

Итак, $M=11neq 0$. Теперь попробуем составить любой минор, порядок которого выше трёх. Чтобы составить минор четвёртого порядка, нам придётся использовать четвёртую строку, однако все элементы этой строки равны нулю. Следовательно, в любом миноре четвёртого порядка будет нулевая строка, а это означает, что все миноры четвёртого порядка равны нулю. Миноры пятого и более высоких порядков составить мы не можем, так как матрица $A$ имеет всего 4 строки.

Мы нашли минор третьего порядка, не равный нулю. При этом все миноры высших порядков равны нулю, следовательно, рассмотренный нами минор – базисный. Строки матрицы $A$, на которых расположены элементы этого минора (первая, вторая и третья), – базисные строки, а первый, третий и четвёртый столбцы матрицы $A$ – базисные столбцы.

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

$$A=left( begin -1 & 2 & 0 & -2 & -14\ 3 & -17 & -3 & 19 & 29\ 5 & -6 & 8 & -9 & 41\ -5 & 11 & 19 & -20 & -98\ 6 & 12 & 20 & 21 & 54\ -7 & 10 & 14 & -36 & 79 end right) $$

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Добавим к набору строк, на которых лежат элементы минора $M$, ещё строку №1, а к набору столбцов – столбец №5. Получим новый минор $M’$ (уже третьего порядка), элементы которого расположены на пересечении строк №1, №2, №5 и столбцов №2, №4, №5. Элементы минора $M$ на рисунке выделены красным цветом, а элементы, которые мы добавляем к минору $M$ – синим:

Минор $M’$ является окаймляющим минором для минора $M$. Аналогично, добавляя к набору строк, на которых лежат элементы минора $M$, строку №4, а к набору столбцов – столбец №3, получим минор $M»$ (минор третьего порядка):

Минор $M»$ также является окаймляющим минором для минора $M$.

Видео:Видеоурок "Минор и алгебраическое дополнение"Скачать

Минор k-го порядка матрицы $A_$. Дополнительный минор. Алгебраическое дополнение к минору квадратной матрицы.

Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.

Для примера рассмотрим квадратную матрицу пятого порядка:

$$ A=left( begin -1 & 2 & 0 & -2 & -14\ 3 & -17 & -3 & 19 & 29\ 5 & -6 & 8 & -9 & 41\ -5 & 11 & 16 & -20 & -98\ -7 & 10 & 14 & -36 & 79 end right) $$

Выберем в ней строки №1 и №3, а также столбцы №2 и №5. На пересечении оных строк и столбцов будут элементы минора $M$ второго порядка. Эти элементы выделены в матрице $A$ зелёным цветом:

Теперь уберём из матрицы $A$ строки №1 и №3 и столбцы №2 и №5, на пересечении которых находятся элементы минора $M$ (элементы убираемых строк и столбцов показаны красным цветом на рисунке ниже). Оставшиеся элементы образуют минор $M’$:

Минор $M’$, порядок которого равен $5-2=3$, является минором, дополнительным к минору $M$.

Словосочетание «алгебраическое дополнение к минору $M$» часто заменяют словосочетанием «алгебраическое дополнение минора $M$».

Для примера рассмотрим матрицу $A$, для которой мы находили минор второго порядка $ M=left| begin 2 & -14 \ -6 & 41 end right| $ и дополнительный к нему минор третьего порядка: $M’=left| begin 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end right|$. Обозначим алгебраическое дополнение минора $M$ как $M^*$. Тогда согласно определению:

Параметр $alpha$ равен сумме номеров строк и столбцов, на которых находится минор $M$. Этот минор расположен на пересечении строк №1, №3 и столбцов №2, №5. Следовательно, $alpha=1+3+2+5=11$. Итак:

$$ M^*=(-1)^cdot M’=-left| begin 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end right|. $$

В принципе, используя формулу №2 из темы вычисления определителей второго и третьего порядков, можно довести вычисления до конца, получив значение $M^*$:

$$ M^*=-left| begin 3 & -3 & 19\ -5 & 16 & -20 \ -7 & 14 & -36 end right|=-30. $$

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Алгебраические дополнения

Определение . Алгебраическим дополнением элемента a_i j определителя D называется его минор, взятый со знаком (-1) i+j .
Алгебраическое дополнение элемента a_i j обозначается через A_i j . Следовательно, A_i j = (-1) i+j M_i j .

Ввод данных
Видеоинструкция

Пример №1 . Дан определитель . Найти минор и алгебраическое дополнение элемента a₂ 1 (выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент a₂ 1 , получим 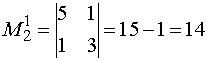. Тогда A₂ 1 = (-1) 1+2 M₂ 1 = -14.
Теорема. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т.е.
D=a i₀ ₁·A i₀ ₁+a i₀ ₂·A i₀ ₂+ . + a i₀ _n·A i₀ _n (*)
где i₀ – фиксировано.
Выражение (*) называют разложением определителя D по элементам строки с номером i₀.
Вычисление определителя n -го порядка сводится к вычислению одного определителя ( n-1 )-го порядка, для чего в какой–либо строке (или столбце) получают ( n -1) нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).

Пример №2 . Покажем нахождение алгебраических дополнений на примере определения обратной матрицы:

Решение находим с помощью калькулятора. Найдем главный определитель.
∆ = 0.73 ∙(0.72 ∙0.92 -(-0.17 ∙(-0.15 )))-(-0.19 ∙(-0.07 ∙0.92 -(-0.17 ∙(-0.12 ))))+(-0.12 ∙(-0.07 ∙(-0.15 )-0.72 ∙(-0.12 ))) = 0.437197
Транспонированная матрица

Алгебраические дополнения

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.

X = x 1 x 2 ⋮ x n — столбец неизвестных,

B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :

A — 1 × A × X = A — 1 × B .

Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Видео:Обратная матрица (2 способа нахождения)Скачать

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2

Записываем систему в виде матричного уравнения А X = B , где

А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

Выражаем из этого уравнения X :

Находим определитель матрицы А :

d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.