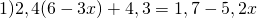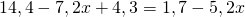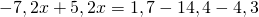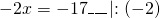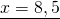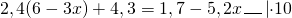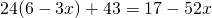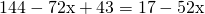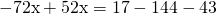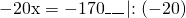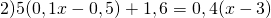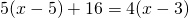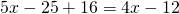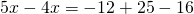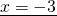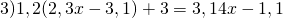Решить уравнение с десятичными дробями и решением

Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Уравнение. 5 класс.Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Видео:УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 классСкачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:Решение уравнений, 6 классСкачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Уравнения с десятичными дробями

Линейные уравнения с десятичными дробями можно решать так же, как и остальные линейные уравнения.

Однако, удобнее сначала уравнение упростить, избавившись от десятичных дробей.

Для начала рассмотрим оба способа решения и сравним их.

Раскрываем скобки. Так как перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках:

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Чтобы перевести десятичные дроби в целые числа, умножим обе части уравнения почленно на 10:

(При умножении произведения 2,4(6-3х) на 10 применяем сочетательное свойство умножения, то есть на 10 мы умножим только первый множитель, 2,4).

Получили линейное уравнение, которое не содержит десятичных дробей. Решаем его:

На мой взгляд, линейные уравнения с десятичными дробями удобнее решать, переводя их в уравнения с целыми числами.

Чтобы избавиться от десятичных дробей, обе части уравнения умножаем на 10. При этом в произведении 5(0,1х-0,5) на 10 умножаем второй множитель, то есть выражение в скобках, а в произведении 0,4(х-3) — первый, то есть 0,4:

Далее — решаем обычное линейное уравнение:

Обе части уравнения умножаем на 100. При этом в произведении 1,2(2,3х-3,1), надо первый множитель 1,2 умножить на 10 и второй множитель (2,3х-3,1) умножить на 10:

Видео:Уравнение с десятичными дробямиСкачать

Рациональные уравнения онлайн калькулятор

Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.

Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.

Видео:Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

Добро пожаловать на сайт Pocket Teacher

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Видео:Решение уравнений и пропорций с десятичными дробямиСкачать

начать

Видео:Решение уравнений с десятичными дробямиСкачать

Рациональные уравнения

В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.

Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.

Действия с рациональными числами обладают свойствами действий с целыми числами.

К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.

Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.

Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».

Делить на ноль в рациональных уравнениях, как и в обычных нельзя.

Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.

Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.

Видео:Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

📹 Видео

Решить уравнение с дробями - Математика - 6 классСкачать

Решение уравнений с дробными числами в 6 классеСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Уравнение на десятичные дроби со скобками и делением. Номер 391г.Скачать

Как решать уравнения с дробью? #shortsСкачать

Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать