Решить уравнение производная равна нулю если функция (6 видео)

Узнать ещё

Знание — сила. Познавательная информация

Содержание

Производная равна нулю на графике функции
Задание №6. Производная. Поведение функции. Первообразная — профильный ЕГЭ по Математике
📽️ Видео

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Производная равна нулю на графике функции

В №7 ЕГЭ несколько видов заданий, в который нужно по графику функции найти точки, в которых производная обращается в нуль.

Как найти, в каких точках производная равна нулю на графике функции?

В точках, в которых производная равна нулю, касательная к графику функции параллельна оси абсцисс.

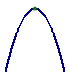
Это могут быть точки экстремума (те из них, в которых производная существует):

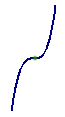
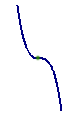
Либо точки перегиба:

В окрестности точки экстремума график лежит по одну сторону от касательной, в окрестности точки перегиба — по разные стороны.

1)На рисунке изображён график функции y=f(x), определённой на интервале (−1; 11). Найдите корень уравнения f'(x)=0.

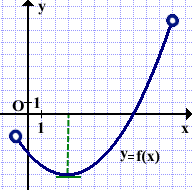
Касательная к графику функции y=f(x) параллельна оси абсцисс в точке x=3.

Следовательно, корнем уравнения f'(x)=0 является x=3.

2)На рисунке изображён график функции y=f(x), определённой на интервале (−4; 20). Найти количество решений уравнения f'(x)=0.

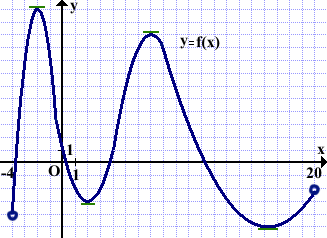
Касательная к графику параллельна оси абсцисс в четырёх точках.

Значит, уравнение f'(x)=0 имеет четыре решения.

3)На рисунке изображен график функции y=f(x), определенной на интервале (−4; 10) . Найдите количество точек, в которых производная функции f(x) равна 0.

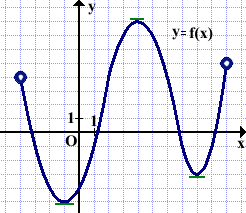
Касательная к графику параллельна оси Ox в трёх точках.

Таким образом, производная функции f(x) равна 0 в трёх точках.

В этих примерах мы рассматривали график функции y=f(x)!

Задания, в которых надо определить в каких точках производная равна нулю на графике производной y=f'(x), решаются иначе!

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Задание №6. Производная. Поведение функции. Первообразная — профильный ЕГЭ по Математике

Необходимая теория:

Задание 6 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.

Геометрический смысл производной

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

возрастает	точка максимума	убывает	точка минимума	возрастает
0	0

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

6. На рисунке изображён график — производной функции , определённой на интервале . В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

8. На рисунке изображен график производной функции , определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Н.С. Шернина, преподаватель Кубанского госуниверситета

1. Производная

Рассмотрим некоторую функцию в двух точках и : и .
Здесь через обозначено некоторое малое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: называется приращением функции.

Если этот предел существует, то функция называется дифференцируемой в точке . Производная функции обозначается (формула 2)

2. Геометрический смысл производной

Рассмотрим график функции .

Из рис.1 видно, что для любых двух точек A и B графика функции можно записать формула 3). В ней — угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует вывод.

3. Уравнение касательной

Выведем уравнение касательной к графику функции в точке . В общем случае уравнение прямой с угловым коэффициентом имеет вид:
Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:
Отсюда следует: .
Подставляя это выражение вместо b, получаем уравнение касательной(формула 4).

4. Механический смысл производной

Рассмотрим простейший случай: движение материальной точки вдоль координатной оси. При этом задан закон движения точки: координата x движущейся точки – это известная функция времени . В течение интервала времени от до точка перемещается на расстояние: .
Её средняя скорость () находится по формуле: . При значение средней скорости стремится к определённой величине, которая в физике называется мгновенной скоростью материальной точки в момент времени . Следовательно, для мгновенной скорости можно записать формулу 5

Если сравнить эту формулу с формулой производной 1, то можно сделать вывод, что

5. Дифференциал и его связь с производной
Дифференциал функции. Геометрический смысл дифференциала

Дифференциал функции – это произведение производной и приращения аргумента (формула 6).

Геометрический смысл дифференциала ясен из рисунка 2.

Здесь . Из можно записать: , где β – угол наклона касательной АС к оси ОХ. Но если , то . Дифференциал CD равен сумме отрезков BС и BD (приращение функции). Но, если , то и отрезок . Значит, дифференциал отличается от производной на бесконечно малую величину.

6. Основные свойства производных и дифференциалов. Производная сложной функции
6.1 Правила дифференцирования функций. Таблица производных простейших элементарных функций.
Если , то , .
Если и — дифференцируемые функции в точке , то можно записать:

Таблица производных простейших элементарных функций

1. ,
где С – постоянное число
2.
Частные случаи:

3.
Частный случай

4.
Частный случай

5.
6.
7.
8.
9.
10.
11.
12.

6.2 Производная сложной функции

Рассмотрим сложную функцию, аргумент которой также является функцией: . Если функция f имеет производную в точке , а функция g имеет производную в точке , то сложная функция h также имеет производную в точке , вычисляемую по формуле:

6.3 Вторая производная

Если производная функции дифференцируема в точке , то её производная называется второй производной функции в точке , и обозначается .

6.4 Правило Лопиталя

Пусть при для функций и, дифференцируемых в некоторой окрестности точки а , выполняются условия. (формулы 7).

Эта теорема называется правилом Лопиталя. Она позволяет вычислять пределы отношения функций, когда и числитель, и знаменатель cтремятся либо к нулю, либо к бесконечности. Правило Лопиталя, как говорят математики, позволяет избавляться от неопределённостей типа: и . Рассмотрите примеры.

При неопределённостях другого типа: , , , , нужно проделать предварительно ряд тождественных преобразований, чтобы привести их к какой-то из двух неопределённостей: либо , либо . После этого можно применять правило Лопиталя. Покажем некоторые из возможных преобразований указанных неопределённостей.

: пусть ,, тогда данная неопределённость приводится к типу посредством следующего преобразования:

: пусть , , тогда данная неопределённость приводится к типу или с помощью преобразований:

остальные неопределённости приводятся к первым двум с помощью логарифмического преобразования:

Если же после применения правила Лопиталя неопределённость типа или осталась, нужно применить его повторно. Многократное применение правила Лопиталя может привести к требуемому результату. Правило Лопиталя применимо и в случае, если .

7. Применение производной в исследовании функций
7.1 Связь между непрерывностью и дифференцируемостью функции

Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной (рисунок 3). Если же функция разрывная в некоторой точке, то она не имеет производной в этой точке.

7.2 Достаточные признаки монотонности функции

Если в каждой точке интервала , то функция возрастает на этом интервале. Если в каждой точке интервала , то функция убывает на этом интервале.

7.3 Теорема Дарбу

Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.Рассмотрите примеры

Следовательно, функция на рисунке 4а возрастает на интервалах и и убывает на интервале . Точка не входит в область определения функции, но по мере приближения x к 0 слагаемое неограниченно возрастает. Поэтому функция также неограниченно возрастает. В точке значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ).

7.4 Критические точки

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум, рис.5а,б).

В точках , (рис.5a) и (рис.5b) производная равна 0. В точках , (рис.5б) производная не существует. Но все они – это точки экстремума.

7.5 Необходимое условие экстремума

Если — точка экстремума функции и производная существует в этой точке, то .

Эта теорема – необходимое условие экстремума. Если же производная функции в некоторой точке равна 0, то это не значит, что функция всегда имеет экстремум в этой точке. Например, производная функции равна 0 при , но эта функция не имеет экстремум в этой точке ( рис.6 ).
С другой стороны, функция , представленная на рис.3, имеет минимум в точке , но в этой точке производной не существует.

7.6 Достаточные условия экстремума

Если производная при переходе через точку меняет свой знак с плюса на минус, то — точка максимума.
Если производная при переходе через точку меняет свой знак с минуса на плюс, то — точка минимума.

7.7 План исследования функции
Для построения графика функции нужно:

Пример . Исследование функции , построение графика
1) область определения (x – любое действительное число); область значений , так как – многочлен нечётной степени;
2) функция не является ни чётной, ни нечётной (докажите самостоятельно);
3) – непериодическая функция (докажите самостоятельно);
4) график функции пересекается с осью Y в точке , так как .
Чтобы найти нули функции нужно решить уравнение: .
Один из его корней очевиден. Другие корни находятся (если они есть!) из решения квадратного уравнения: . Оно получено делением многочлена на двучлен . Легко проверить, что два других корня: и . Таким образом, нулями функции являются:-2, -1 и 1.

5) Это означает, что числовая ось делится этими корнями на четыре интервала знакопостоянства, внутри которых функция сохраняет свой знак. Этот же результат может быть получен разложением многочлена на множители:
. Затем надо оценить знак произведения методом интервалов.
6) Производная не имеет точек, в которых она не существует, поэтому её область определения R (все действительные числа); нули – это корни уравнения: .
Эти корни: .
Функция имеет две критические точки и три интервала монотонности: .
Полученные результаты сведены в таблицу. В ней стрелками обозначены выводы о возрастании функции или её убывании (наклонная стрелка вверх или вниз) внутри соответствующего интервала.

Теперь мы располагаем полной информацией для построения графика данной функции (рис. 8).

7.8 Выпуклость, вогнутость, точки перегиба

Функция называется выпуклой на интервале , если её график на этом интервале лежит ниже касательной, проведенной к кривой в любой точке , при этом .
Функция называется вогнутой на интервале , если её график на этом интервале лежит выше касательной, проведенной к кривой в любой точке , при этом .

7.9 Достаточное условие вогнутости (выпуклости) функции

Пусть функция дважды дифференцируема (имеет вторую производную) на интервале , тогда: если для любого , то функция является вогнутой на интервале ; если для любого , то функция является выпуклой на интервале .
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба существует вторая производная , то .
Пример : Рассмотрим график функции . Эта функция является вогнутой при и выпуклой при .
В самом деле, , но при и при , следовательно, при и при , откуда следует, что функция является вогнутой при и выпуклой при . Тогда является точкой перегиба функции .