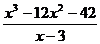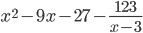//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Теорема Безу. Практическая часть. 10 класс.Скачать
Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена
Видео:Теорема Безу. 10 класс.Скачать
Немного теории.
Видео:Схема Горнера. 10 класс.Скачать
Деление многочлена на многочлен (двучлен) столбиком (уголком)
В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).
Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов ( f(x) ) и ( g(x) ), ( g(x) neq 0 ), существуют единственные полиномы ( q(x) ) и ( r(x) ), такие что
$$ frac = q(x)+frac $$
причем ( r(x) ) имеет более низкую степень, чем ( g(x) ).
Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного ( q(x) ) и остатка ( r(x) ) для заданных делимого ( f(x) ) и ненулевого делителя ( g(x) )
Видео:Теорема Безу. Схема Горнера. Практическая часть. 10 класс.Скачать
Пример
Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ frac $$
Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой ( (x^3/x = x^2) )
|
|
2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого ( (x^2 cdot (x-3) = x^3-3x^2) )
|
|
3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой ( (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) )
|
|
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
|
|
5. Повторяем шаг 4.
|
|
6. Конец алгоритма.
Таким образом, многочлен ( q(x)=x^2-9x-27 ) — частное деления многочленов, а ( r(x)=-123 ) — остаток от деления многочленов.
Результат деления многочленов можно записать в виде двух равенств:
( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 )
или
$$ frac = x^2-9x-27 + frac $$
Видео:✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать
Деление многочленов столбиком
Алгоритм деления в столбик применяется в частности при нахождении интегралов.
- Решение онлайн
- Видеоинструкция
Пример деления в столбик . Найти частное деления и остаток многочлена:
№1.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 |
| -9x 2 -42 |
№2.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 |
№3.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x -27 |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 | |
| -27x + 81 | |
| -123 |
Целая часть: x 2 -9x -27
Остаток: -123
Таким образом, ответ можно записать как: 
см. также и другие примеры решение столбиком.
Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1
Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)
Видео:Теорема БезуСкачать
Деление многочленов онлайн
Онлайн калькулятор осуществляет деление многочленов двумя различными способами: делением в столбик и методом неопределенных коэффициентов. Для работы калькулятора введите исходные данные своей задачи.
Осуществить деление многочлена
методом деления в столбик.
Метод деления в столбик рассмотрим на следующем примере. Пусть нам требуется разделить многочлен
Сразу необходимо отметить, что:
деление многочленов возможно только в том случае, если степень многочлена делимого больше или равна степени многочлена делителя.
В нашем случае указанное условие выполняется т.к. степень многочлена делимого равна трём, а степень многочлена делителя — двум.
Чтобы осуществить деление многочленов, запишем многочлен делимое слева от вертикальной черты, а многочлен делитель — справа:
Далее, разделим слагаемое со старшей степенью многочлена делителя на слагаемое со старшей степенью многочлена делимого :
Запишем полученный результат (частное от деления) справа под чертой:
Теперь, умножаем на многочлен делитель , получаем:
Записываем полученный результат слева под многочленом делимым:
Вычитаем из многочлена делимого полученный результат:
Записываем полученный многочлен в столбик:
Далее, процедура повторяется, т.е. мы делим слагаемое со старшей степенью полученного многочлена ( ) на слагаемое со старшей степенью многочлена делителя ( ), и т.д., в результате получаем:
Процесс деления останавливается, когда степень многочлена остатка меньше степени многочлена делителя. Это условие описано выше.
Записываем полученный результат следующим образом. Сначала записываем частное (многочлен справа под чертой) равное , затем прибавляем к нему дробь, числителем которой является многочлен остаток равный (тот многочлен, который остался после всех вычитаний слева снизу в столбике) а знаменателем — многочлен делитель . В результате получаем:
Другим способом деления многочленов является метод неопределенных коэффициентов. Рассмотрим его на том же самом примере. В общем случае, результат деления многочленов можно записать в следующем виде:
где — многочлен частное, степень которого равна разности степеней многочлена делимого и многочлена делителя, т.е. в нашем случае — единице. — многочлен остаток, степень которого не больше степени многочлена делителя, т.е. в нашем случае — не больше единице.
Теперь, запишем многочлен в общем виде:
— неизвестные пока коэффициенты.
Тоже самое для многочлена :
— неизвестные пока коэффициенты.
Таким образом, получаем следующее равенство:
Итак, нам нужно определить неизвестные коэффициенты и . Для этого домножаем обе части приведенного выше равенства на знаменатель — многочлен делитель , получаем:
Раскрываем скобки, приводим подобные слагаемые:
Для того, чтобы сохранить верное равенство, нам нужно приравнять коэффициенты при одинаковых степенях . В результате получаем следующую систему линейных уравнений:
В результате решения этой системы, получаем следующие значения коэффициентов:
Подставляем значения полученных коэффициентов и исходное равенство:
Как видно, данный результат полностью совпадает с результатом, полученным методом деления в столбик.
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать
Другие полезные разделы:
Видео:Теорема Безу. Схема Горнера. Практическая часть. 10 класс.Скачать
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
📺 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Деление многочленов. Теорема Безу. Объяснение на пальцахСкачать
Теорема Безу. Схема Горнера. Практическая часть. 10 класс.Скачать
Метод неопределенных коэффициентов. 10 класс.Скачать
Теорема Безу и разложение многочлена на множителиСкачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Деление многочлена на многочлен. 10 класс.Скачать
Деление многочлена на многочленСкачать
Математика без Ху!ни. Деление многочлена на многочлен.Скачать
Теорема Безу в задании #14 ЕГЭ профиль (как делить многочлены в столбик)Скачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Математика| Разложение квадратного трехчлена на множители.Скачать
