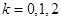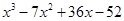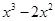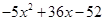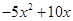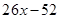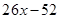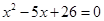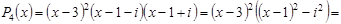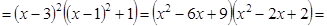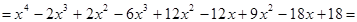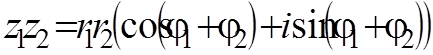Решить уравнение на множестве комплексных чисел x2 4x 13 0

Найду корень уравнения: x^2-4*x+13=0

Решение

Это уравнение вида

Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$x_ = frac <sqrt- b>$$
$$x_ = frac <- sqrt- b>$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -4$$
$$c = 13$$
, то

© Контрольная работа РУ — калькуляторы онлайн

Видео:Комплексные корни квадратного уравненияСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Простое решение сложного уравнения ➜ Решите уравнение ➜ x⁴-2x³-13x²+14x-3=0Скачать

Решить комплексное уравнение по математике

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Сегодня вы можете в режиме онлайн решить уравнение с комплексными числами, однако сложно будет проверить правильность результата, не имея представления о комплексных числах, поэтому мы ознакомим вас с числами данного вида.

Комплексное число — это выражение вида [x+yi.] В данном выражении [x,y] — действительные числа, [а i] — мнимая единица, квадрат которого -1, [i^2=-1.] [b] называют мнимой частью комплексного числа [a=x+yi.] В случае, если [y=0,] то вместо [x+0i] пишут [x.] Над данным типом чисел можно выполнять абсолютно все арифметические действия, что и над действительными.

Например, вам необходимо решить квадратное уравнение:

Изначально необходимо вычислить дискриминант:

Поскольку дискриминант отрицательный, то в действительных числах его решить нельзя. Однако можно извлечь корень в комплексных числах:

Получаем 2 корня:

— сопряженные комплексные корни.

Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Где можно решить комплексное уравнение онлайн с решением?

Решить комплексное уравнение онлайн решателем вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Примеры решения алгебраических уравнений на множестве комплексных чисел (Приведите примеры решения алгебраических уравнений на множестве комплексных чисел)

1. Алгебраические уравнения первой степени:

, – единственный простой корень.

.

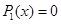
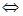
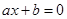
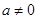
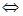
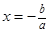
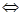
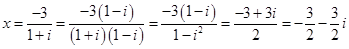
Ответ: .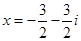

2. Квадратные уравнения:

, – всегда имеет два корня (различных или равных).

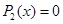
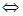
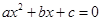
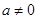
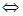
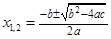
1) .

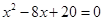
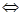
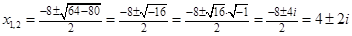
Ответ: .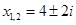

2) .

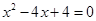
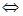
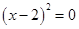
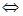
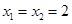
Ответ: .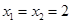

3) , .

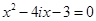
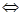
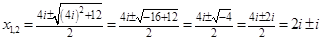
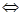
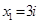
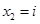
Ответ: , .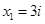

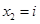
3. Двучленные уравнения степени :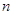

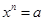
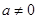
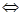
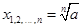
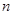
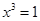
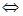
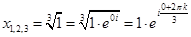
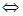
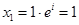
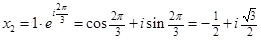
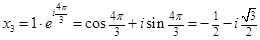
, – всегда имеет различных корней.

,

;

;

.

Ответ: , .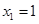

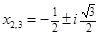
4. Решить кубическое уравнение .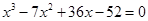

Уравнение третьей степени 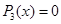имеет три корня (действительные или комплексные), при этом нужно считать каждый корень столько раз, какова его кратность. Так как все коэффициенты данного уравнения являются действительными числами, то комплексные корни уравнения, если они есть, будут парными комплексно сопряженными.

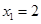
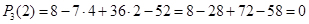
Подбором находим первый корень уравнения , так как .

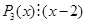
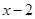
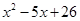
По следствию из теоремы Безу . Вычисляем это деление «в столбик»:

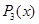
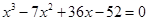
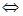
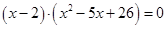
Представляя теперь многочлен в виде произведения линейно и квадратного множителя, получим:

.

Другие корни находим как корни квадратного уравнения:

.

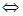
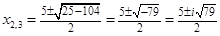
Ответ: , .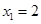

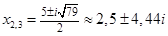
5. Составить алгебраическое уравнение наименьшей степени с действительными коэффициентами, если известно, что числа x1 = 3 и x2 = 1 + i являются его корнями, причем x1 является двукратным корнем, а x2 — простым.

Число 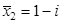тоже является корнем уравнения, т.к. коэффициенты уравнения должны быть действительными.

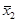
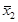
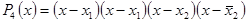
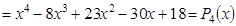
Всего искомое уравнение имеет 4 корня: x1, x1, x2, . Поэтому его степень равна 4. Составляем многочлен 4-й степени с нулями x1, x1, x2, по формуле (6):

Þ

.

Искомое уравнение имеет вид P4(x) = 0.

Ответ: .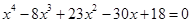

Вопросы для самопроверки

1. Сформулируйте определение комплексного числа

2. Что называется комплексным числом?

3. Какое название или смысл имеет формула?

4. Поясните смысл обозначений в этой формуле:

5. ⌂ .

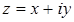
6. Что такое мнимая единица?

7. Что такое действительная часть комплексного числа z?

8. Что такое мнимая часть комплексного числа z?

9. Что такое комплексно сопряженное число?

10. Что такое противоположное число?

11. Что такое комплексный ноль?

12. Что такое чисто мнимое число?

13. Сформулируйте смысл комплексного равенства.

14. В чём состоит геометрическое изображение комплексных чисел?

15. Что такое модуль и аргумент комплексного числа?

16. Что называется модулем комплексного числа?

17. Что такое аргумент комплексного числа?

18. Какое название или смысл имеет формула?

19. Поясните смысл обозначений в этой формуле:

20. ⌂ .

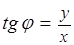
21. Что такое алгебраическая и тригонометрическая формы комплексного числа?

22. Какое название или смысл имеет формула?

23. Поясните смысл обозначений в этой формуле:

24. ⌂ .

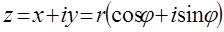
25. Что называется алгебраической формой комплексного числа?

26. Что называется тригонометрической формой комплексного числа?

27. Дайте определения и перечислите основные свойства арифметических действий над комплексными числами.

28. Какое название или смысл имеет формула?

29. Поясните смысл обозначений в этой формуле:

31. Какое название или смысл имеет формула?

32. Поясните смысл обозначений в этой формуле:

33. ⌂ .

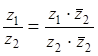
34. Какое название или смысл имеет формула?

35. Поясните смысл обозначений в этой формуле:

36. ⌂ .

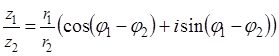
37. Что такое формула Муавра?

38. Какое название или смысл имеет формула?

39. Поясните смысл обозначений в этой формуле:

40. ⌂ .

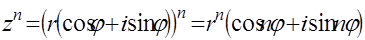
41. Что называется корнем степени n из комплексного числа?

42. Какое название или смысл имеет формула?

43. Поясните смысл обозначений в этой формуле:

44. ⌂ .

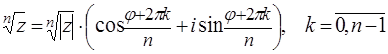
45. Что называется показательной формой комплексного числа?

46. Какое название или смысл имеет формула?

47. Поясните смысл обозначений в этой формуле:

48. ⌂ .

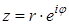
49. Что такое формулы Эйлера?

50. Какое название или смысл имеет формула?

51. Поясните смысл обозначений в этой формуле:

52. ⌂ .

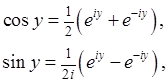
53. Что называется целой функцией?

54. Что называется алгебраическим многочленом?

55. Что называется полиномом?

56. Что такое степень многочлена?

57. Что такое коэффициенты многочлена?

58. Что называется алгебраическим уравнением n-й степени?

59. Что называется нулем функции?

60. Что называется корнем уравнения?

61. Перечислите основные свойства многочленов.

62. Сформулируйте свойство о тождественном равенстве многочленов.

63. Сформулируйте свойство о делении многочлена на разность (x – х0).

64. Сформулируйте теорему теорема Безу.

65. Какое название или смысл имеет формула?

66. Поясните смысл обозначений в этой формуле:

67. ⌂ .

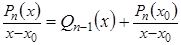
68. Сформулируйте свойство о существовании нуля многочлена.

69. Сформулируйте теорему теорема алгебры основная.

70. Какое название или смысл имеет формула?

71. Поясните смысл обозначений в этой формуле:

72. ⌂ .

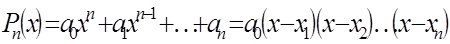
73. Что называется k-кратным нулем многочлена?

74. Что называется простым нулем многочлена?

75. Сформулируйте свойство о количестве корней алгебраического уравнения.

76. Сформулируйте свойство о комплексных корнях алгебраического уравнения

77. с действительными коэффициентами.

78. Сформулируйте свойство о разложении многочлена с действительными коэффициентами на линейные и квадратичные множители.

79. Приведите примеры решения алгебраических уравнений на множестве комплексных чисел

k-кратным нулем многочлена называется. (стр. 18)

алгебраическим многочленом называется. (стр. 14)

алгебраическим уравнением n-й степени называется. (стр. 14)

алгебраической формой комплексного числа называется. (стр. 5)

аргумент комплексного числа это. (стр. 4)

действительная часть комплексного числа z это. (стр. 2)

комплексно сопряженное число это. (стр. 2)

комплексный ноль это. (стр. 2)

комплексным числом называется. (стр. 2)

корнем степени n из комплексного числа называется. (стр. 10)

корнем уравнения называется. (стр. 14)

коэффициенты многочлена это. (стр. 14)

мнимая единица это. (стр. 2)

мнимая часть комплексного числа z это. (стр. 2)

модулем комплексного числа называется. (стр. 4)

нулем функции называется. (стр. 14)

показательной формой комплексного числа называется. (стр. 11)

полиномом называется. (стр. 14)

простым нулем многочлена называется. (стр. 18)

противоположное число это. (стр. 2)

степень многочлена это. (стр. 14)

тригонометрической формой комплексного числа называется. (стр. 5)

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Калькулятор Уравнений. Решение Уравнений Онлайн

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

💡 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Математика это не ИсламСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Решение уравнений, 6 классСкачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Решение квадратных уравнений в поле комплексных чиселСкачать

Биквадратное уравнение. Комплексные корни.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Решение биквадратных уравнений. 8 класс.Скачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать