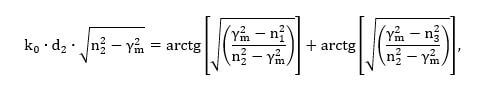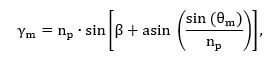Решить уравнение на интервале в матлаб (4 видео)

Решение нелинейных уравнений в Matlab

Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.

Содержание

Общая информация
Стандартные функции Matlab
Метод перебора Matlab
Метод простых итераций Matlab
Метод половинного деления Matlab
Заключение
Численные методы решения уравнений в среде MatLab
Листинг программы для решения уравнений вида f(x)=x в среде MatLab
Листинг программы для решения уравнений вида f(x,y)=y в среде MatLab
Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1
💥 Видео

Общая информация

Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.

В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:

Метод перебора
Метод простых итераций
Метод половинного деления

Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.

Стандартные функции Matlab

Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.

И сразу же разберем пример:

Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.

Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.

Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график:

Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.

С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:

Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.

Метод перебора Matlab

Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].

Теперь реализуем метод перебора в Matlab:

Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:

Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.

Метод простых итераций Matlab

Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме x_n= g(x_n-1). То есть итерационно проходим от предыдущего значения к последующему.

Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.

Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.

А вот и вывод программы:

Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.

Метод половинного деления Matlab

Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.

Перейдем к реализации метода в Matlab:

Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:

Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.

Заключение

Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.

На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Численные методы решения уравнений в среде MatLab

В этом посте я расскажу о численных методах решения уравнений, что очень удобно для их расчёта на компьютере. Приведу 3 вида и 3 примера кода, для каждого вида соответственно, а также расскажу о предостерегающих трудностях и путях их решения.

Иногда нам приходится решать уравнения, кому-то по работе, а кому-то понадобилась для домашних нужд — назовём это так. В школе нас учили, что для решения уравнения, необходимо выразить искомую переменную и тогда мы получим символьное решение уравнения, а если вместо букв поставить числа, то получим численное решение того или иного уравнения. Однако, бывают такие уравнения, в которых нельзя явно выразить искомую переменную, например, уравнение ниже.

Решать такие уравнения приходиться численно, то есть получая ответ в виде числа, а если вам нужна зависимость, то придётся задать диапазон начальных условий и получить, соответственно, диапазон значений искомого параметра.

Предлагаю вам ознакомиться с моей презентацией, а после чего прочитать комментарии и пояснения к ней ниже. Также, в конце записи я опубликовал листинги программ для расчёта указанными методами в среде MatLab.

При решении уравнений 2 или 3 типа, может возникнуть ситуация , когда из большого шага между двумя значениями x и(или) y, мы можем не достичь требуемой точности и тогда результат будет не предсказуем. Для избежания таких случаев предлагаю использовать не сравнение результата с заданным уровнем точности, а сравнение точностей для каждого значения переменной и выбор значения с наибольшей точностью. Подробнее расскажу на примере кода. Рекомендую использовать следующей алгоритм действий для уравнений типа f(x)=const:

разбиваете заданный диапазон значений на n равных интервалов и получаете n+1 значений x
решаете уравнение для каждого значения х
выбираете то значение х_i, при котором точность максимальна.
из п. 3 следует, что точное решение находится между х_i-1 и х_i+1. Устанавливаете новый диапазон значений для x от х_i-1 до х_i+1, сохраняя то же число интервалов.
Вновь расчитываете уравнение для нового интервала с новым шагом
Повторяете указанные действия до тех пор, пока интервал значений х не будет достаточно мал, чтобы получить требуемую точность вычислений.

Аналогичный алгоритм, лишь с некоторым поправками, можно использовать и для решения уравнений вида f(x,y)=y.

Листинг программы для решения уравнений вида f(x)=x в среде MatLab

Если кому интересно, то ниже производится решение следующего уравнения относительно γ.

Листинг программы для решения уравнений вида f(x,y)=y в среде MatLab

Этот код решает следующее уравнение относительно θ.

На выходе данной программы получаем массив значений угла θ. Границы диапазона θ от 61.7 до 61.8 найдены путём последовательных приближений. Сначала уравнение решалось для всех гамма в пределах угла от 1 до 90 с шагом в 1 градус, затем диапазон сужался по тому же принципу, что и в случае с предыдущем кодом, и действия повторялись до достижения требуемой точности.

Если у вас есть какие-либо вопросы, замечания или предложения, то их в комментариях к данному посту! Удачных вам математических расчётов!

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

каким образом записывать системы диффуров
как задать начальные условия
временной интервал
какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink.

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла. Об этом мы поговорим чуть позже и на конкретном примере.

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

решение дифференциального уравнения первого порядка.
решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие. Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции. И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов.

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой. Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться.

Видеообзор по теме решения систем Д/У доступен по ссылке.