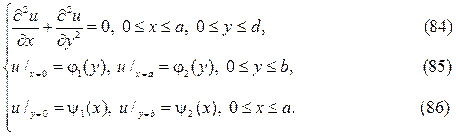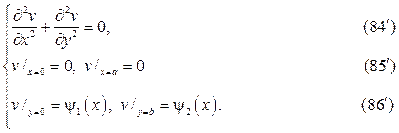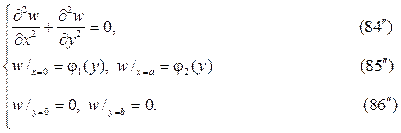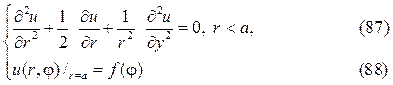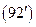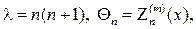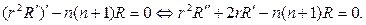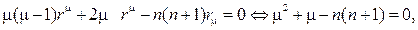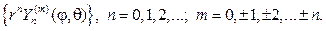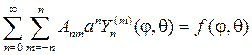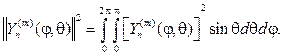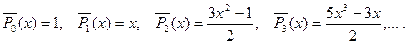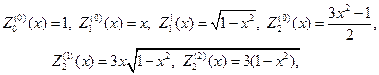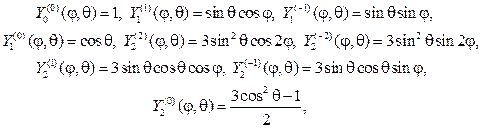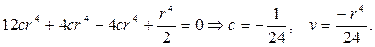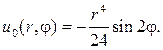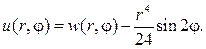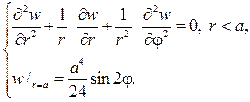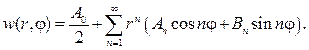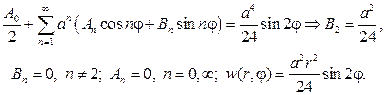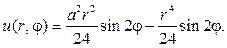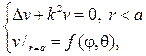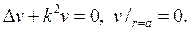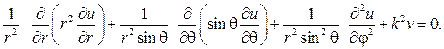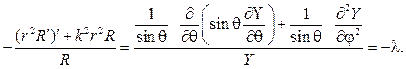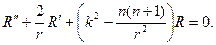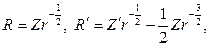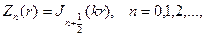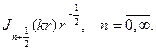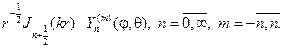ЭЛЛИПТИЧЕСКОГО ТИПА
Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма 
следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач
Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.
Рассмотрим задачу Дирихле для круга
где f(j)кусочно-непрерывная функция.
Следуя схеме метода Фурье полагаем
подставляем в (87) и разделяем переменные. В результате получим ра -венство
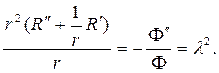
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма 
откуда следует, что
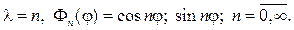
Возвращаясь к (80), решаем уравнение для радианальной функции. При
r 2 R² + rR¢ 
решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение
m(m 
Видео:11. Уравнение Лапласа в прямоугольном параллелепипедеСкачать

Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции
R0(r) = 1; lnr.
С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге
Если предположить, что ряд
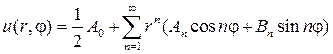
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем
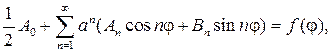
откуда с учетом формул коэффициентов Фурье следует
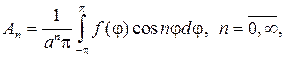
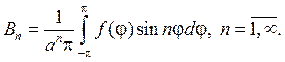

Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в
центре круга r=0.
Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом
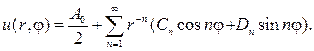
В случае кругового кольца a 2 q= 1-x 2 , найдем
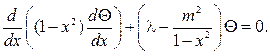
Соответственно и граничные условия (105) перейдут после замены в неравенства
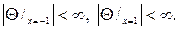
Задача (104¢) 
и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):
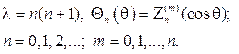
Составив произведения функций (106) на найденные выше функции Fm(j), получим множество решений уравнения (102)
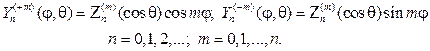
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.
Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m1¹m2 или n1¹n2
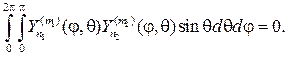
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции
Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки
откуда находим значения m=n; 
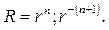
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:
Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами
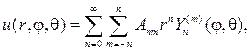
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.
Для нахождения коэффициентов Аnm подставим (110) в (100), тогда
и с учетом (108) найдем
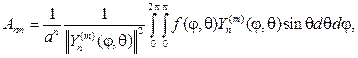
Последний интеграл вычисляется и при m=0 :
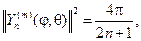
если же |m| ³ 1, то имеем

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).
Видео:Решение волнового уравнения в прямоугольникеСкачать

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам
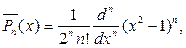
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.
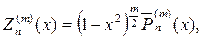
в частности будем иметь
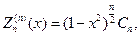
где Сn определенная константа.
С учетом (107), (115) и (116) выпишем несколько сферических функций:
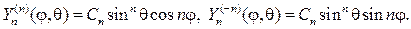
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд
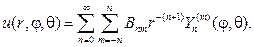
Общий вид гармонической функции в шаровом слое a 4 , и получим
Таким образом, частным решением будет функция
Вводим новую неизвестную функцию w(r,j) , полагая
Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа
Согласно (93), решение этой задачи дается формулой
Подставляя ее в граничное условие, получим
Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

Ответом в задаче будет функция
254. Найдите решение первой краевой задачи для уравнения Гельмгольца
предполагая, что k не является собственным значением задачи
Р е ш е н и е. Запишем уравнение в сферических координатах
Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:
Функция 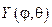
Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение
Выполняя в этом уравнении замену
придем к соотношению относительно новой функции Z(r):
Последнее уравнение в качестве ограниченных в окрестности нуля
r=0 решений имеет бесселевы функции
соответственно будем иметь набор радиальных функций
Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Составляем ряд с числовыми коэффициентами
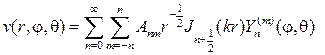
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a
где d = 4 при m = 0 и d =2 при
При найденных коэффициентах Anm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.
255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1
🌟 Видео
Метод Лапласа решения ДУСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать

Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать
Уравнения математической физики. Уравнение Лапласа. Часть 1Скачать

Колыбасова В.В. - Методы математической физики. Семинары - 3. Ур.Лапласа в прямоугольных координатахСкачать

7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать

Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

9. Уравнение ПуассонаСкачать

Уравнение ЛапласаСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 5. Уравнение Лапласа в полярных коорд. 1Скачать

УМФ, 01.12, решение задач Лапласа и Пуассона в случае неоднородных граничных условийСкачать
Решение уравнения Лапласа в шареСкачать