Решить уравнение комбинированным методом онлайн (5 видео)

Метод хорд

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе хорд под калькулятором.

Содержание

Метод хорд
Метод хорд
Нелинейные уравнения
Решение нелинейных уравнений
Системы уравнений по-шагам
Результат
Примеры систем уравнений
Правила ввода
🎬 Видео

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

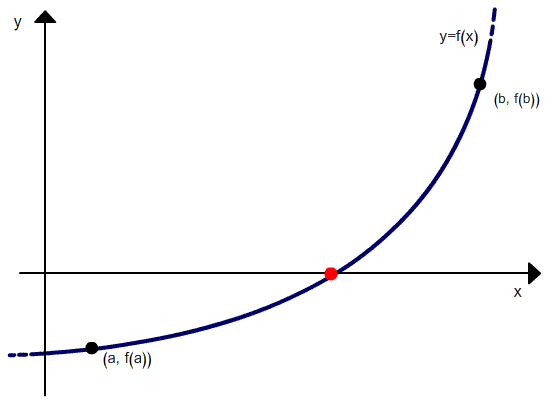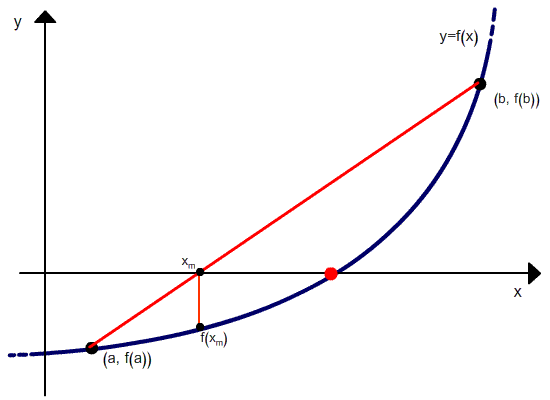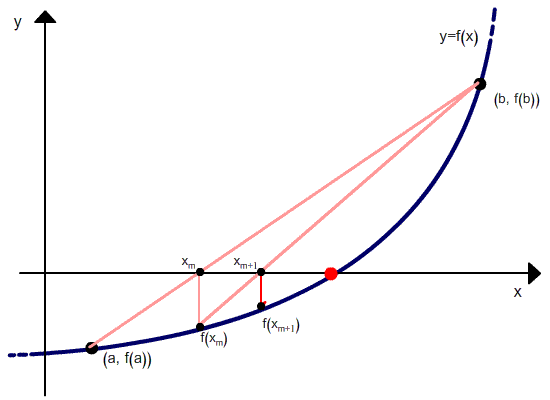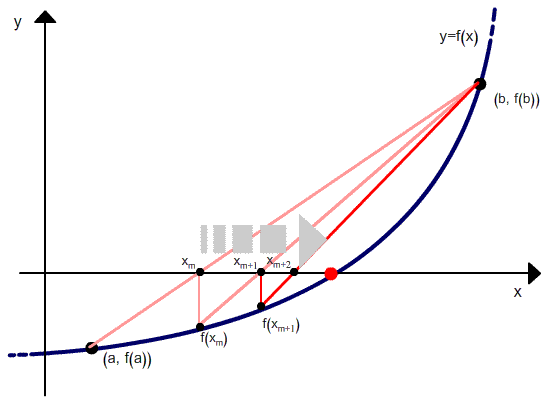
Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Нелинейные уравнения

Уравнение вида f (x) = 0, где f (x) — некая нелинейная функция, называется нелинейным. Виды таких уравнений: алгебраические, где функция алгебраическая, и трансцендентные, в которых функция может быть тригонометрическая, показательная и т.д.

При решении нелинейных уравнений используются прямые (точные) и итерационные (численные) методы. Решить точным методом — значит, представить решение в виде формулы, по которой находят корни уравнения. Для уравнений выше 4-й степени невозможно написать аналитическое решение.
Бывает, что в уравнении присутствуют приближенные коэффициенты. В этом случае для решения уравнения применяют итерационные методы, где заранее задается точность. Решение уравнения такими методами предполагает нахождение корней (или их отсутствие) и определение их значения с заданной точностью.

Решение нелинейных уравнений

Корнем уравнения f (x) = 0 является такое значение с, при котором f© = 0.
Уравнение f (x) = 0 имеет одно решение на отрезке |а;b| при условии, что функция f (x):
— непрерывна и монотонна на данном отрезке;
— значения функции на концах отрезка с разными знаками, т.е. f (а)• f (b) меньше 0.

Вычисление корня уравнения f (x) = 0 путем использования численных методов:
— устанавливаем знаки функции в предельных точках области ее существования
х = а, х = b;
— определяем приближенное значение корня или промежутка, в котором он находится;
— уточняем приближенное значение до определенной точности.

Данный калькулятор станет для вас надежным помощником при решении нелинейных уравнений онлайн. Вам потребуется лишь ввести исходные данные в окна калькулятора.

Видео:Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

Системы уравнений по-шагам

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Результат

Примеры систем уравнений

Метод Гаусса
Метод Крамера
Прямой метод
Система нелинейных уравнений

Указанные выше примеры содержат также:

квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
asinh(x), acosh(x), atanh(x), actanh(x)
число Пи pi
комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте: