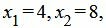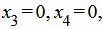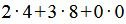- Воспользуйтесь нашим простым онлайн-графическим калькулятором для графического решения с пошаговым объяснением.
- Добавьте калькулятор алгебры в закладки вашего браузера
- Как пользоваться графическим калькулятором
- Шаг 1
- Шаг 2
- Шаг 3
- Что такое графический калькулятор
- Симплекс метод онлайн
- Предупреждение
- Симплекс метод
- Примеры решения ЗЛП симплекс методом
- Примеры решения ЗЛП методом искусственного базиса
- Универсальный математический калькулятор
- Онлайн калькулятор уравнений, интегралов, производных, пределов, дробей и пр.
- Пояснения к калькулятору
- Упрощение выражений, раскрытие скобок, разложение многочленов на множители
- Решение уравнений и неравенств
- Решение систем уравнений и неравенств
- Вычисление выражений с логарифмами
- Вычисление пределов функций
- Решение интегралов
- Вычисление производных
- Действия над комплексными числами
- 🌟 Видео
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Воспользуйтесь нашим простым онлайн-графическим калькулятором для графического решения с пошаговым объяснением.
- Главная
- Графический калькулятор
Добавьте калькулятор алгебры в закладки вашего браузера
1. Для Windows или Linux — нажмите Ctrl + D .
2. Для MacOS — нажмите Cmd + D .
3. Для iPhone (Safari) — нажмите и удерживайте , затем нажмите Добавить закладку
4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки
Видео:Casio fx-9860 SOLVE решение любых уравнений на графическом калькулятореСкачать

Как пользоваться графическим калькулятором
Шаг 1
Введите свою математическую задачу в поле ввода.
Шаг 2
Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.
Шаг 3
Во всплывающем окне выберите нужную операцию. Вы также можете воспользоваться поиском.
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Что такое графический калькулятор
Предлагаем вашему вниманию сервис для рисования функциональных схем в режиме онлайн. Используйте левый столбец для ввода функций. Вы можете ввести его вручную или с помощью виртуальной клавиатуры внизу окна. Чтобы увеличить окно с графиком, вы можете скрыть как левый столбец, так и виртуальную клавиатуру. Чтобы построить график функции онлайн, вам просто нужно ввести свою функцию в специальное поле и щелкнуть где-нибудь за его пределами. После этого график введенной функции будет построен автоматически.
Графики функций — это совокупность всех точек, представляющих геометрический вид функции; более того, x — любая точка из области определения функции, а все y — точки, равные соответствующим значениям функции. Другими словами, график функции y = f (x) — это совокупность всех точек, абсциссы и ординаты которых соответствуют уравнению y = f (x).
В большинстве случаев невозможно отобразить график функции абсолютно точно, так как точек бесконечно много, сложно найти все точки графика функции. В таких случаях можно построить приблизительный график функции. Чем больше точек будет учтено, тем точнее будет график.
Этот сервис создан для помощи школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для построения графиков функций (условных и параметрических) и графиков по точкам (графики по значениям), а также графиков функций в режиме онлайн. в полярной системе координат. Самый удобный сервис, позволяющий построить интерактивный график функций онлайн. Благодаря этому график можно масштабировать, а также перемещать по координатной плоскости, что позволит не только получить общее представление о построении этого графика, но и более подробно изучить поведение графика функции. в разделах.
Калькулятор алгебры с расширенными функциями. Удобный и простой инженерный калькулятор с богатым арсеналом возможностей для математических расчетов и при этом с приятным и интуитивно понятным интерфейсом.
Видео:Калькулятор не поможет решить уравнение ИКС УМНОЖИТЬ НА ИКС РАВНО ДВАСкачать

Симплекс метод онлайн
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Как посчитать любое уравнение! Шок!!Скачать

Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Видео:Функция SOLVE.Обучающее видеоСкачать

Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
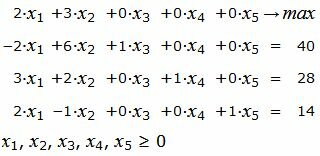 |
Р е ш е н и е. Матрица коэффициентов 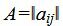
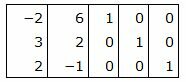 |
Правая часть ограничений системы уравнений имеет вид:
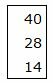 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные 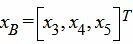
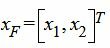
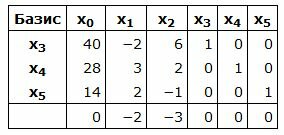 |
Запишем текущий опорный план:
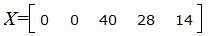 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем 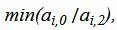
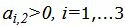
Симплекс таблица примет следующий вид:
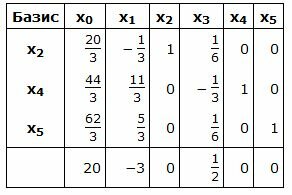 |
Запишем текущий опорный план:
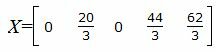 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем 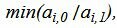
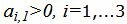
Симплекс таблица примет следующий вид:
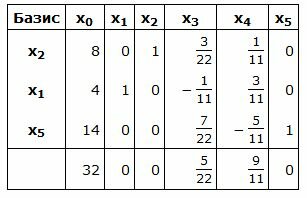 |
Запишем текущий опорный план:
 |
Текущий опорный план является оптимальным, так как в строках 4 под переменными 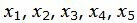
Решение можно записать так: 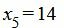
Значение целевой функции в данной точке: F(X)=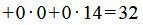
Пример 2. Найти максимум функции
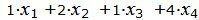 |
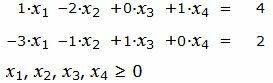 |
Р е ш е н и е. Матрица коэффициентов 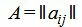
 |
Правая часть ограничений системы уравнений имеет вид:
 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1:
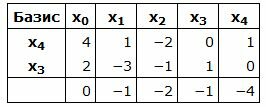 |
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
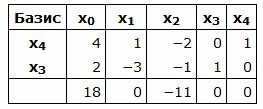 |
Запишем текущий опорный план:
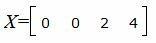 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем 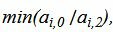
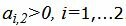
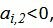
Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
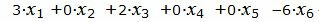 |
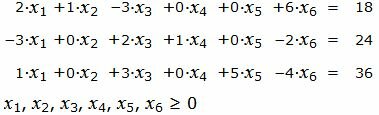 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
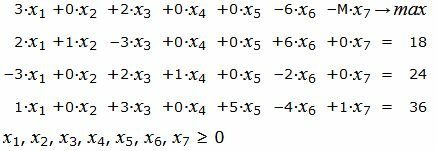 |
Матрица коэффициентов 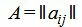
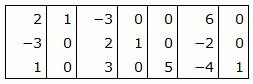 |
Правая часть ограничений системы уравнений имеет вид:
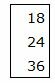 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
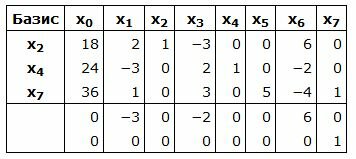 |
Базисные векторы 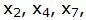
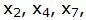
Обнулим все элементы столбца 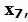
Симплекс таблица примет вид:
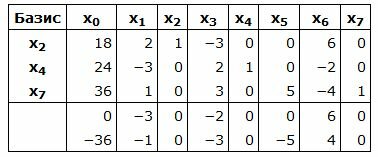 |
Запишем текущий опорный план:
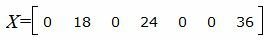 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор 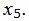
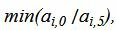
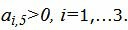
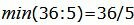
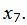
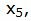
Симплекс таблица примет следующий вид:
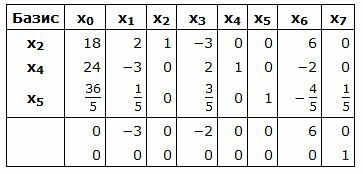 |
Запишем текущий опорный план:
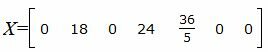 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор 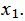

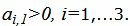
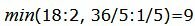
Симплекс таблица примет следующий вид:
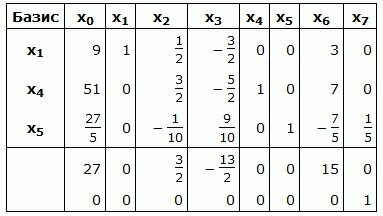 |
Запишем текущий опорный план:
 |
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем 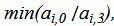
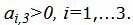
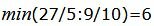
Симплекс таблица примет следующий вид:
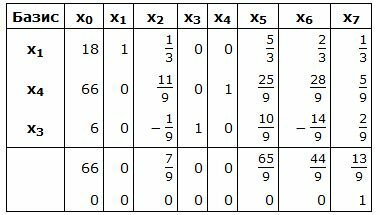 |
Запишем текущий опорный план:
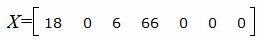 |
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными 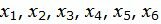
Решение исходной задачи можно записать так:
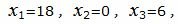 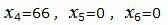 . . |
Значение целевой функции в данной точке:
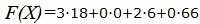 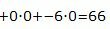 . . |
Пример 2. Найти оптимальный план задачи линейного программирования:
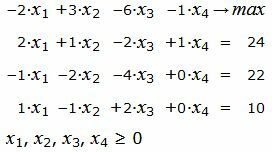 |
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
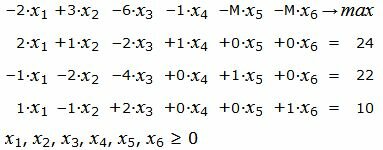 |
Матрица коэффициентов 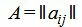
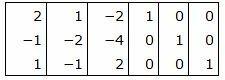 |
Правая часть ограничений системы уравнений имеет вид:
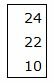 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
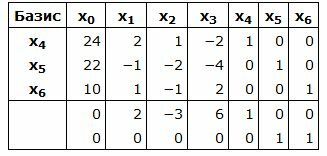 |
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
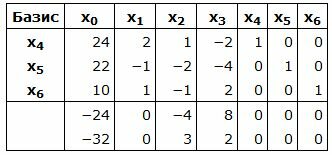 |
Запишем текущий опорный план:
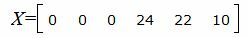 |
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Видео:Графический метод решения задачи линейного программирования (ЗЛП)Скачать

Универсальный математический калькулятор
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам.
Также универсальный калькулятор умеет производить действия со скобками, дробями, тригонометрическими функциями, возведение в любую степень и многое другое (смотрите примеры ниже).
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Онлайн калькулятор уравнений, интегралов, производных, пределов, дробей и пр.
Разделитель системы уравнений
Натуральный логарифм и предел:
Видео:Гайд на калькулятор | СASIO FX-991 EX PLUSСкачать

Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵ .
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и → .
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½ , ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби. Для ввода целой части смешанного числа необходимо установить курсор перед дробью с помощью клавиши ← и ввести число.
- Ввод числа в n-ой степени и квадратного корня прозводится кнопками a b и √ соответственно. Завершить ввод значения в степени или в корне можно клавишей → .
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Упрощение выражений, раскрытие скобок, разложение многочленов на множители
Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.
Видео:Программируемые графические калькуляторы! Casio fx-cg50Скачать

Решение уравнений и неравенств
Математический калькулятор может решать уравнения и неравентства относительно переменной «x». Если есть необходимость найти другую переменную, например «y», то следует просто поменять их местами в выражении. Ввод переменных «x»,»y»,»z» производится в группе xyz нажатием соответствующих кнопок x , y , z .
Примеры решений уравнений и неравенств:
Видео:Casio fx-CG50 решает дифференциальные уравненияСкачать

Решение систем уравнений и неравенств
Системы уравнений и неравенств также решаются с помощью онлайн калькулятора. Чтобы задать систему необходимо ввести уравнения/неравенства, разделяя их точкой с запятой с помощью кнопки ; .
Примеры вычислений систем уравнений и неравенств:
Видео:Графический метод решения уравнений 8 классСкачать

Вычисление выражений с логарифмами
В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$log_a left(bright) = frac$$ Например, $$log_ left(5x-1right) = frac$$
Примеры решений выражений с логарифмами:
Видео:Решение системы уравнений графическим методомСкачать

Вычисление пределов функций
Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim .
Примеры решений пределов:
Видео:Калькулятор для чайников | Гайд по калькулятору для ЕГЭ по ФизикеСкачать

Решение интегралов
Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
∫ f(x) — для неопределенного интеграла;
b a∫ f(x) — для определенного интеграла.
В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.
Примеры вычислений интегралов:
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Вычисление производных
Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) — производная первого порядка;
f»(x) — производная второго порядка;
f»'(x) — производная третьего порядка.
f n (x) — производная любого n-о порядка.
Видео:Обзор инженерного калькулятораСкачать

Действия над комплексными числами
Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i
🌟 Видео
Математика это не ИсламСкачать

Графический метод решения задач линейного программирования | Высшая математика TutorOnlineСкачать