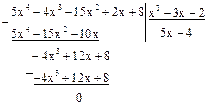Решить уравнение если известно что его корни образуют арифметическую прогрессию

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

ЛАБОРАТОРНАЯ РАБОТА №4 КОРНИ МНОГОЧЛЕНОВ, КРАТНЫЕ МНОЖИТЕЛИ

Определение 1. Если многочлен f(x) обращается в нуль при подстановке в него числа с вместо неизвестного, то с называется корнем многочлена f(x) (или уравнения f(x)=0).

Пример 1. f(x)=x 5 +2x 3 -3x.

Число 1 является корнем f(x), а число 2 не является корнем f(x), так как f(1)=1 5 +2∙1 3 -3∙1=0, а f(2)=2 5 +2∙2 3 -3∙2=42≠0.

Оказывается, корни многочлена связаны с его делителями.

Число с тогда и только тогда является корнем многочлена f(x), когда f(х) делится на х-с.

Определение 2. Если с — корень многочлена f(х), то f(х) делится на х-с. Тогда найдется натуральное число k, что f(х) делится на (х-с) k , но не делится на (х-с) k+1 . Такое число k называется кратностью корня с многочлена f(х), а сам корень с — k-кратным корнем этого многочлена. Если k=1, то корень с называют простым.

Для нахождения кратности k корня с многочлена f(х) применяют теорему:

Если число с является k-кратным корнем многочлена f(х), то при k>1 оно будет (k-1)-кратным корнем первой производной этого многочлена; если же k=1, то с не будет служить корнем для f ‘(х).

Следствие. k-кратный корень многочлена f(х) впервые не будет служить корнем для k-й производной.

Пример 2.Убедиться, что число 2 является корнем многочлена f(х)=х 4 -4х 3 +16х-16. Определить его кратность.

Решение. Число 2 является корнем f(х), так как 2 4 -4∙2 3 +16∙2-16=0.

f ‘(x)=4x 3 -12x 2 +16, f ‘(2)=4∙2 3 -12∙2 2 +16=0;

f »(x)=12x 2 -24x, f »(2)=12∙2 2 -24∙2=0;

Число 2 впервые не является корнем f»'(х), поэтому число 2 является трехкратным корнем многочлена f(х).

Пусть дан многочлен f(х) степени n≥1 со старшим коэффициентом 1: f(х)=х n +a₁x n -1 +…+a_n-1x+a_n и α₁. α_n – его корни. Корни многочлена и его коэффициенты связаны формулами, которые называют формулами Виета:

Формулы Виета облегчают написание многочлена по заданным его корням.

Пример 3. Найти многочлен, имеющий простые корни 2; 3 и двукратный корень –1.

Решение. Найдем коэффициенты многочлена:

Искомый многочлен есть х 4 –3х 3 –3х 2 –7х+6.

Определение 3. Многочлен f(х)ÌР[x] степени n приводим над полем Р, если он может быть разложен в произведение двух множителей φ(х) и ψ(х) из Р[x], степени которых меньше n:

f(x)ÎP[x] называют неприводимым над полем Р, если в любом его разложении на множители из Р[x] один из множителей имеет степень 0, другой – степень n.

Имеют место следующие теоремы:

Всякий многочлен ненулевой степени f(х) из кольца Р[x] разлагается в произведение неприводимых множителей из Р[x] однозначно с точностью до множителей нулевой степени.

Отсюда легко следует, что для всякого многочлена f(х)ÎР[x] степени n, n≥1, существует следующее разложение на неприводимые множители:

, (2)

где — неприводимые многочлены из P[x] со старшими коэффициентами, равными единице. Такое разложение для многочлена однозначно.

Неприводимые множители, входящие в такое разложение, не обязаны быть все различными. Если неприводимый многочлен встречается ровно k раз в разложении (2), то он называется k-кратным множителем многочлена f(х).Если множитель Р(х) входит в это разложение только один раз, то он называется простым множителем для f(х).

Если в разложении (2) одинаковые множители собрать вместе, то это разложение можно записать в следующем виде:

, (3)

где множители Р₁(х),…,Р_r(x) уже все различные. Показатели k₁,…,k_r здесь равны кратностям соответствующих множителей. Разложение (3) можно записать в виде:

, (4)

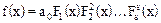
где F₁(x) – произведение всех простых неприводимых множителей, — произведение всех двукратных неприводимых множителей и т.д. в разложении (3). Если в разложении (3) нет m-кратных множителей, то множитель считается равным единице.

Многочлены F₁(x),…,F_s(x) для многочлена f(x) над числовыми полями можно найти, пользуясь понятием производной, алгоритмом Евклида из формулированной ранее теоремы (о связи с производной) следующим образом:

Поэтому получаем

Таким образом, для многочлена f(x) мы можем найти множители .

Если для многочлена f(x) надо найти множители F₁(x),…,F_s(x) его разложения (4), то говорят, что надо отделить его кратные множители.

Пример 4.Отделить кратные множители f(x)=х 5 -х 4 -5х 3 +х 2 +8х+4.

Решение. Находим НОД f(x) и f ‘(x)=5x 4 -4x 3 -15x 2 +2x+8.

(производим деление).

(производим деление).

Поэтому получаем F₃(x)=v₃(x)=x+1,

Таким образом, многочлен f(x) имеет разложение f(x)=(х-2) 2 (х+1) 3 . В разложении (3) многочлена f(x) простых множителей нет, двукратный множитель х-2 и трехкратный множитель х+1.

Замечание 1.Этот способ ничего не дает в том случае, если все неприводимые множители многочлена f(x) простые (получим тождество f(x)=F₁(x)).

Замечание 2.Этот способ позволяет определить кратности всех корней произвольного многочлена.

ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ

Вариант 1

1. Убедиться, что многочлен 3х 4 -5х 3 +3х 2 +4х-2 имеет корень 1+i. Найти остальные корни многочлена.

2. Отделить кратные множители х 5 +5х 4 -5х 3 -45х 2 +108.

3. Найти многочлен наименьшей степени, корнями которого являются: 5, i, i+3.

Вариант 2

1. Чему равен показатель кратности корня х₀=2 для многочлена f(x)=x 5 -7х 4 +12х 3 +16х 2 -64х+48? Найти остальные его корни.

2. Отделить кратные множители х 5 -6х 4 +16х 3 -24х 2 +20х-8.

3. Определить соотношение между коэффициентами уравнения x 3 +px+q=0, если его корни х₁, х₂, х₃, удовлетворяют соотношению .

Вариант 3

1. Чему равен показатель кратности корня х₀=4 для многочлена х 4 -7х 3 +9х 2 +8х+16? Найти остальные корни.

2. Отделить кратные множители х 6 -2х 5 -х 4 -2х 3 +5х 2 +4х+4.

3. Определить λ так, чтобы один из корней уравнения равнялся удвоенному другому: x 3 -7x+λ=0.

Вариант 4

1. Показать, что х=3 является корнем многочлена f(x)=х 4 -6х 3 +10х 2 -6х+9. Определить его кратность и найти остальные корни.

2. Отделить кратные множители многочлена х 5 +6х 4 +13х 3 +14х 2 +12х+8.

3. Сумма двух корней уравнения 2х 3 -х 2 -7х+λ=0 равна 1. Найти λ.

Вариант 5

1. Показать, что х₀=-2 является корнем многочлена х 4 +х 3 -18х 2 -52х-40. Определить его кратность и найти остальные корни.

2. Отделить кратные множители многочлена f(x)=х 5 -5х 4 -5х 3 +45х 2 -108.

3. Найти многочлен наименьшей степени по данным корням 1, 2, 3, 1+i.

Вариант 6

1. Найти условие, при котором многочлен х 5 +ах 4 +b имеет двойной корень, отличный от нуля.

2. Отделить кратные множители многочлена х 6 +15х 4 -8х 3 +51х 2 -72х+27.

Вариант 7

1. Показать, что х=-2 является корнем многочлена 4х 5 +24х 4 +47х 3 +26х 2 -12х-8. Найти кратность корня и найти остальные корни многочлена.

2. Отделить кратные множители многочлена х 4 +х 3 -3х 2 -5х-2.

3. Найти сумму квадратов корней уравнения 2х 3 -2х 2 -4х-1.

Вариант 8

1. Доказать, что х=1 является корнем многочлена х 6 -х 5 -4х 4 +6х 3 +х 2 -5х+2. Определить его кратность. Найти остальные корни многочлена.

2. Отделить кратные множители многочлена х 5 -3х 4 +4х 3 -4х 2 +3х-1.

3. Один из корней многочлена в два раза больше другого. Найти корни многочлена f(х)=х 3 -7х 2 +14х+λ.

Вариант 9

1. Найти условие, при котором многочлен х 5 +10ах 3 +5bх+с имеет тройной корень, отличный от нуля.

2. Отделить кратные множители многочлена х 7 -3х 6 +5х 5 -7х 4 +7х 3 -5х 2 +3х-1.

3. Решить уравнение х 3 -6х 2 +qх+2=0, если известно, что его корни образуют арифметическую прогрессию.

Вариант 10

1. Показать, что х=3 является корнем многочлена f(x)=х 4 -12х 3 +53х 2 -102х+72. Определить кратность корня, найти другие корни многочлена.

2. Отделить кратные множители многочлена х 6 -4х 4 -16х 2 +16.

3. Найти многочлен с действительными коэффициентами наименьшей степени по данным корням 1, 2+i, 3.

Вариант 11

1. Показать, что х=2 является корнем многочлена х 5 -6х 4 +13х 3 -14х 2 +12х-8. Найти его кратность и остальные корни.

2. Отделить кратные множители многочлена х 4 +х 3 -3х 2 -5х-2.

3. Составить многочлен наименьшей степени, если известны его корни х₁=2, x₂=1-i, x₃=3.

Вариант 12

1. Показать, что х=-1 является корнем многочлена х 4 +х 3 -3х 2 -5х-2. Найти его кратность и остальные корни многочлена.

2. Отделить кратные множители многочлена х 5 -3х 4 +4х 3 -4х 2 +3х-1.

3. Составить многочлен наименьшей степени, если известны его корни х₁=i, x₂=2+i, x₃=x₄=2.

Вариант 13

1. Чему равен показатель кратности корня х₀=4 для многочлена х 4 -7х 3 +9х 2 +8х+16? Найти остальные корни многочлена.

2. Отделить кратные множители многочлена х 6 -2х 5 -х 4 -2х 3 +5х 2 +4х+4.

3. Определить λ так, чтобы один из корней уравнения х 3 -7х+λ=0 равнялся удвоенному другому.

Видео:Арифметическая прогрессия 9 класс. Формулы, о которых вы не знали | МатематикаСкачать

«Формулы Виета как один из способов решения кубических уравнений » (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

При умножении левой и правой частей на двучлен x + b получается уравнение:

.

Новые уравнения имеют в обоих случаях те же положительные корни, что и исходные уравнения.

В уравнении ,

которое может иметь два корня, Виет определяет коэффициенты так, чтобы корни имели данные значения. Если обозначить последние через у и z, то

, .

Аналогичное определение коэффициентов Виет предпринимает и для уравнений вида

,

где m + n − четное число, а m – нечетное число.

Важно то, что Виет распространил известные ранее частные преобразования на все алгебраические уравнения. Подстановку , которую Кардано применял для исключения из кубического уравнения члена второй степени, он применил к уравнениям любой степени. Известную Кардано обратную подстановку

Виет использовал, чтобы освободиться в некоторых случаях от отрицательных коэффициентов и иррациональностей.

Например, уравнение

Виет подстановкой преобразовывал к уравнению вида

.

Подстановкой Виет преобразовывал уравнение n-й степени так, что коэффициент при члене -й степени становился равным b, в то время, как старший коэффициент оставался равным единице.

Подстановку Виет применял, чтобы избавиться от дробных коэффициентов.

Особый интерес представляет исследование Виета по составлению уравнений из линейных множителей и по установлению связей между корнями уравнения и его коэффициентами.

Рассмотрим ход рассуждений Виета на следующих примерах.

Пусть х1 и х2 − корни приведенного квадратного уравнения

.

Перемножим двучлены и :

,

тогда, сравнение с исходным уравнением дает систему равенств:

Выполняя аналогичные действия для приведенного кубического уравнения

,

считая х1 , х2 и х3 корнями исходного кубического уравнения, получаем:

,

следовательно, имеет место система равенств

Такой результат для квадратного уравнения был известен Кардано (а в случае положительных корней – еще раньше). Кардано отметил свойство корней кубического уравнения относительно коэффициента при х2, но никакого обоснования в общем виде он дать не мог. Это сделал Виет для любого уравнения до пятой степени включительно.

Кардано в ту пору, когда еще не знал метода дель Ферро – Тартальи, решал некоторые уравнения третьей степени разложением на множители. Например, в уравнении

он прибавлял к обеим частям уравнения выражение , а затем преобразовывал исходное уравнение к виду ,

сокращал на двучлен (так как не учитывал отрицательные корни) и получал квадратное уравнение .

При нахождении положительного корня кубического уравнения

Кардано складывал его почленно с уравнением

,

и получал квадратное уравнение делением на двучлен . Такое преобразование позволило Кардано установить, что коэффициент при члене второй степени в правой части исходного кубического уравнения равен сумме его корней. Это был первый шаг к установлению зависимости между корнями и коэффициентами алгебраического уравнения.

Виет составил полные уравнения с заданными положительными корнями вплоть до пятой степени и показал, как образуются коэффициенты при , , и т. д. (при этом коэффициент при старшей степени Виет считал равным 1 или (−1)). Он установил, что эти коэффициенты при условии, что свободный член в правой части должен был стоять со знаком «+», представляют собой взятые с чередующимися знаками суммы: самих корней, попарных произведений корней, произведений корней, взятых по три и т. д.

Работа, в которой Виет подробно рассмотрел это утверждение, до нас не дошла. Неизвестно, как он поступал в том случае, когда уравнение имело отрицательные корни. Скорее всего, это не представляло для Виета особых трудностей: достаточно было в исходном уравнении сделать замену

и можно оперировать с положительными корнями нового уравнения. Такие примеры в его работах встречались. Например, если уравнение

имеет два положительных корня х1 и х2 , то уравнение

имеет один положительный корень , причем .

Тогда

В исследованиях Виета встречались начала теории симметрических многочленов и разложения многочленов на линейные множители, что вскоре привело к открытию основной теоремы алгебры о числе корней уравнения произвольной натуральной степени.

Задачи математиков связанных с кубическим уравнением

Задача. Доказать, что если дано кубическое уравнение

,

то a, b, c – корни этого уравнения. Проверить на уравнениях:

1) ;

2) .

Решение. Пусть х = а , тогда

.

Раскрывая скобки и приводя подобные члены, получаем тождество:

Аналогично производится проверка чисел b и с.

1) .

Легко видеть, что при х = 1. Следовательно, числа 1, 2, 3 являются корнями уравнения (1).

2) .

Легко видеть, что при х = 2. Следовательно, числа 2, −2, 4 являются корнями уравнения (2).

Шлемильх Оскар (1832-1901)известный немецкий математик, имя которого связано с выражением остаточного члена ряда Тейлора; автор весьма полезного двухтомного курса по математике.

Задача. Решите кубическое уравнение

если его корни составляют:

а) арифметическую прогрессию;

б) геометрическую прогрессию.

Решение. Известно, что между корнями и коэффициентами кубического уравнения существует следующая зависимость (формулы Виета):

а) Если корни уравнения составляют арифметическую прогрессию, то имеем дополнительное условие:

Тогда из (1) и (4) следует: ;

из (1) и (3) : ; ,

откуда , .

Если подставить найденные корни в (2) , то получится условие, которому должны удовлетворять коэффициенты для того, чтобы кубическое уравнение имело корни, представляющие арифметическую прогрессию: .

Обратно, если имеется указанная связь между коэффициентами кубического уравнения, то его корни будут членами арифметической прогрессии.

б) Если корни уравнения составляют геометрическую прогрессию, то имеем дополнительное условие: х1 : х2 = х3 : х4 . (5)

Тогда из (5) и (3) следует: ; (6)

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Решить уравнение если известно что его корни образуют арифметическую прогрессию

Вопрос по математике:

Найти корни уравнения x^3+3x^2-6x+a=0,если известно, что оно имеет три различных действительных корня, образующих геометрическую прогрессию.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Выведем формулы Виета для уравнения третьей степени:

Т.к. корни образуют геометрическую прогрессию, то, справедливо:

Найдём знаменатель геометрической прогрессии и один из членов:

Само уравнение принимает вид .

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

💥 Видео

Как за 10 минут понять СЛОЖНЕЙШУЮ ТЕМУ в Алгебре? Геометрическая прогрессияСкачать

Уравнение и его корни. Математика. АлгебраСкачать

9 класс, 23 урок, Арифметическая прогрессияСкачать

10 класс. Алгебра. Преобразование выражений, содержащих арифметические квадратные корни.Скачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Математика Найти три числа образующих геометрическую прогрессию если известно что их произведениеСкачать

Решение биквадратных уравнений. 8 класс.Скачать

АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать

8 класс. Квадратное уравнение и его корни. Алгебра.Скачать

Арифметическая и геометрическая прогрессия | Математика TutorOnlineСкачать

Алгебра 9 класс. Как найти арифметическую прогрессию, зная сумму и произведение некоторых её членов.Скачать

9 класс, 24 урок, Геометрическая прогрессияСкачать

АЛГЕБРА 9 класс: Целое уравнение и его корни | ВидеоурокСкачать

Задание №1 "Решите методом группировки" по теме "Целое уравнение и его корни". Алгебра 9 классСкачать

Составьте квадратное уравнение, корнями которого являются числаСкачать

#25_Самое сложное задание 14 ОГЭ 2021 // Арифметическая прогрессия на ОГЭ. Задача про шарыСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать