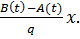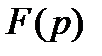Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Займемся решением первой смешанной задачи для уравнения теплопроводности: найти решение и(х, t) уравнения удовлетворяющее начальному условию и граничным условиям Начнем с простейшей задачи: найти решение u(x,t) однородного уравнения удовлетворяющее начальному условию и нулевым (однородным) граничным условиям Метод Фурье для уравнения теплопроводности.
Будем искать нетривиальные решения уравнения (4), удовлетворяющие граничным условиям (6), в виде Псдстаапя в форме (7) в уравнение (4), получим или откуда имеем два обыжювенных дифференциальных уравнения Чтобы получить нетривиальные решения и(х, *) вида (7), удовлетворяющие граничным условиям (6), необходимо найти нетривиальные решения уравнения (10), удовлетворяющие граничным условиям.
Таким образом, для определения фунмдои Х(х) мы приходим к задаче на собственные значения: найти те значения параметра А, при которых существуют нетривиальные решения задачи Эта задача была рассмотрена в предыдущей главе. Там было показано, что только при существуют нетривиальные решения При А = А„ общее решение уравнения (9) имеет вид удовлетворяют уравнению (4) и граничным условиям (6). Образуем формальный ряд.
Потребовав, чтобы функция и(х> t), определяемая формулой (12), удовлетворяла начальному условию , получим Ряд (13) представляет собой разложение заданной функции в ряд Фурье по синусам в интервале (О, I). Коэффициенты а„ разложения определяются по известным формулам Метод Фурье для уравнения теплопроводности Предположим, что Тогдаряд (13) с коэффициентами, определяемыми по формулам (14), будет сходиться к функции абсолютно и равномерно.
Так как при то ряд при также сходится абсолютно и равномерно.
Поэтому функция и(х, t) — сумма ряда (12) — непрерывна в области и удовлетворяет начальному и граничному условиям. Остается показать, что функция и(х, t) удовлетворяет уравнению (4) в области 0. Для этого достаточно показать, что ряды, полученные из (12) почленным дифференцированием по t один раз и почленным дифференцированием по х два раза, также абсолютно и равномерно сходятся при.
Но это следует из того, что при любом t > 0 если п достаточно велико. Единственность решения задачи (4)-(6) и непрерывная зависимость решения от начальной функции были уже установлены ранее. Таким образом, для t > 0 задача (4)-(6) поставлена корректно; напротив, для отрицательных t зада ча эта некорректна. Замечание.
В отличие отдомового уравнения уравнение неомметрично огноситн о времени t: если заменить t на -t, то получаем уравнение другого вида описывает необратимые процессы: Мы можем предсказать, каким станет данное и через промежуток времени данной t, но мы не можем с уверенностью сказать, какн м было это и за время t до рассматриваемого момента. Это раолич иемежду предсказание м и предысторией типично для параболического ура внения и не имеет места, например, для волнового уравн сния; в случае последнего заглянуть в прошлое так же легко, как и в будущее.
Возможно вам будут полезны данные страницы:
- Пример:
- Решение задач:
- Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными
- Условие
- Нужно полное решение этой работы?
- Решение
- Зарегистрируйся, чтобы продолжить изучение работы
- Введение 3 page. Задание 8.Решить смешанную задачу для уравнения теплопроводности с кусочно-гладкими начальными и нулевыми граничными условиями первого рода методом разделения
- 💥 Видео
Пример:
Найти распределение температуры в однородном стерве длины ж, если начальная температура стержня и на концах стержня поддерживается нулевая температура. 4 Задача сводится к решению уравнения при начальном условии и граничных условиях Применяя метод Фурье, ищем нетривиальные решения уравнения (15), удовлетворяющие граничным условиям (17), в виде Подставляя u(x,t) в форме (18) в уравнение (15) и разделяя переменные, получим откуда Собственные значения задачи . собственные функции Хп(х) = мп пх.
При А = А„ общее решение уравнения (19) имеет вид Tn(t) = апе а п так что Решение задачи (15)—(17) ищем в виде ряда Потребовав выполнения начального условия (16), получим откуда . Поэтому решением исходной задачи будет фунхция 2. Рассмотрим теперь следующую задачу: найти решение гх(ж, t) неоднородного уравнения _ удовДстворя ющее начальному условию и однородным граничным услови м Предположим, что функци / непрерывна, имеет непрерывную производ-ную и при всех t > 0 выполняется условие .
Решение задач:
Решение задачи (1)-(3) будем искать в виде где определим как решение задачи а функци — как решение задачи Задача (8)—(10) рассмотрена в п. 1. Будем искать решение v(x, t) задачи (5)-(7) в виде ряда по собстве нным функциям < краевой задачи . Подсгааяяя t) в виде в уравнение (5), получим Разложим функцию /ОМ) в ряд Фурье по синусам, где Сравнивая два разложения (12) и (13) функции /(х, t) в ряд Фурье, получаем ! Пользуясь начальным условием для v(x, t).
| Метод Фурье для уравнения теплопроводности. |
Находим, что Решения уравнений (15) при начальных условиях (16) имеют вид: Подставляя найденные выражения для Tn(t) в ряд (11), получим решение Функция будет решением исходной задачи (1)-(3). 3. Рассмотрим задачу: найти в области решение уравнения при начальном условии и неоднородных граничных условиях Непосредственно метод Фурье неприменим из-за неоднородности условий (20).
Введем новую неизвестную функцию v(x, t), положив где Тогда решение задачи (18)—(20) сведется к решению задачи (1)-(3), рассмотренной в п. 2, для функции v(x, J). Упражнения 1. Задан бесконечный однородный стержень. Покажи те, что если начальная температура то влобой момент температура стержня 2. Ко|рцы стержня длиной ж поддерживаются при температуре, равной нулю. Начальная температура определяется формулой Определите температуру стержня для любого момента времени t > 0. 3.
Концы стержня длиной I поддерживаются при температуре, равной нулю. Начальная температура стержня определяется формулой Определите температуру стержня для любого момента времени t > 0. 4. Концы стержня длиной I поддерживаются при температуре, равной нулю. Начальное распределение температуры Определите температуру стержня для любого момента времени t > 0. Ответы
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными
- Реферат.Справочник
- Решенные задачи по высшей математике
- Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными
Условие
Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевыми начальными и граничными условиями:
Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Нужно полное решение этой работы?
Решение
Данное уравнение является неоднородным уравнением параболического типа (уравнением теплопроводности) с однородными граничными и начальными условиями.
Найдем вначале собственные функции соответствующей однородной задачи:
Решаем задачу методом Фурье.
Положим
.
Вычислив производные и и, подставив их в уравнение, получим
.Последнее равенство выполняется только в том случае, если обе части его не зависят ни от х, ни от t, т.е. представляют собой одну и туже постоянную, которую обозначим за , т.е.
.
Отсюда получаем два обыкновенных однородных линейных уравнений первого и второго порядка
и
.
Для того чтобы получить не равные нулю решения, удовлетворяющие граничным условиям, необходимо найти нетривиальные решения, удовлетворяющие граничным условиям
.
Воспользовавшись ими, получаем
Получаем задачу Штурма-Лиувилля:
Решаем ее
Зарегистрируйся, чтобы продолжить изучение работы
.
Составим характеристическое уравнение: . Его решения: .
Рассмотрим 3 различных случая.
1) λ 0.
В этом случае и общее решение уравнения имеет вид
.
Подставляем граничные условия:
.
Система будет иметь ненулевое решение, если С2≠0, .
Отсюда
.
Получили собственные значения
Оплатите решение задач или закажите уникальную работу на похожую тему
Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

Введение 3 page. Задание 8.Решить смешанную задачу для уравнения теплопроводности с кусочно-гладкими начальными и нулевыми граничными условиями первого рода методом разделения
Задание 8.Решить смешанную задачу для уравнения теплопроводности с кусочно-гладкими начальными и нулевыми граничными условиями первого рода методом разделения переменных
8.1. 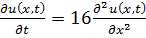 , 0 , 0 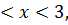  u(x,t) u(x,t) 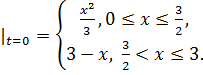 u(x,t) u(x,t)  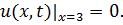 | 8.2. 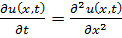 , 0 , 0 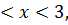  u(x,t) u(x,t) 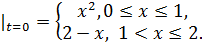 u(x,t) u(x,t)  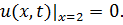 |
8.3. 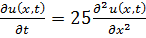 , 0 , 0 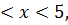  u(x,t) u(x,t) 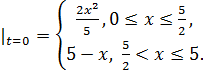 u(x,t) u(x,t)   | 8.4. 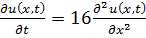 , 0 , 0 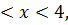  u(x,t) u(x,t) 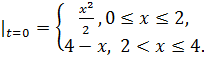 u(x,t) u(x,t)  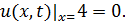 |
8.5. 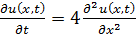 , 0 , 0 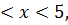  u(x,t) u(x,t) 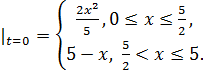 u(x,t) u(x,t)   | 8.6. 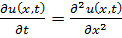 , 0 , 0 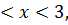  u(x,t) u(x,t) 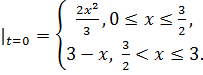 u(x,t) u(x,t)  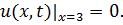 |
8.7. 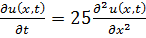 , 0 , 0   u(x,t) u(x,t) 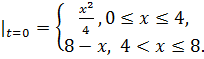 u(x,t) u(x,t)   | 8.8. 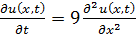 , 0 , 0 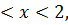  u(x,t) u(x,t) 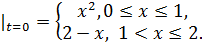 u(x,t) u(x,t)  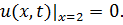 |
8.9. 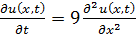 , 0 , 0 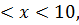  u(x,t) u(x,t) 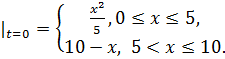 u(x,t) u(x,t)  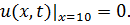 | 8.10. 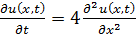 , 0 , 0 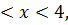  u(x,t) u(x,t) 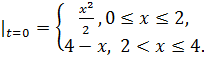 u(x,t) u(x,t)  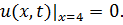 |
8.11. 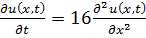 , 0 , 0 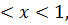  u(x,t) u(x,t) 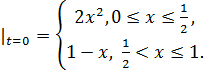 u(x,t) u(x,t)  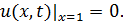 | 8.12. 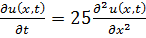 , 0 , 0 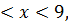  u(x,t) u(x,t) 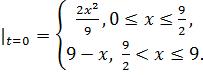 u(x,t) u(x,t)  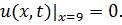 |
8.13. 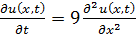 , 0 , 0 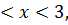  u(x,t) u(x,t) 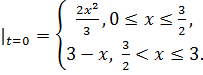 u(x,t) u(x,t)  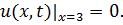 | 8.14. 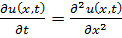 , 0 , 0 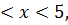  u(x,t) u(x,t) 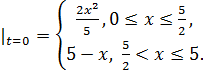 u(x,t) u(x,t)   |
8.15. 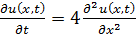 , 0 , 0 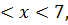  u(x,t) u(x,t) 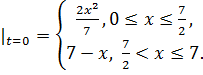 u(x,t) u(x,t)  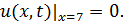 | 8.16. 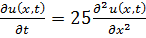 , 0 , 0 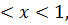  u(x,t) u(x,t) 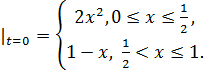 u(x,t) u(x,t)  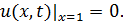 |
8.17. 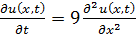 , 0 , 0 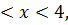  u(x,t) u(x,t) 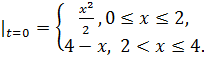 u(x,t) u(x,t)  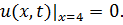 | 8.18. 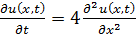 , 0 , 0 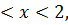  u(x,t) u(x,t) 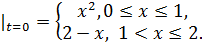 u(x,t) u(x,t)  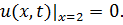 |
8.19. 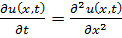 , 0 , 0 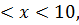  u(x,t) u(x,t) 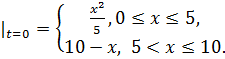 u(x,t) u(x,t)  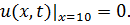 | 8.20. 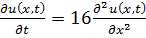 , 0 , 0   u(x,t) u(x,t) 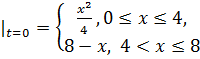 u(x,t) u(x,t)   |
8.21. 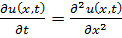 , 0 , 0 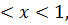  u(x,t) u(x,t) 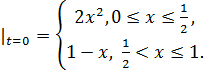 u(x,t) u(x,t)  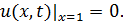 | 8.22. 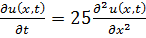 , 0 , 0 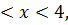  u(x,t) u(x,t) 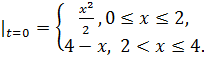 u(x,t) u(x,t)  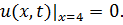 |
8.23. 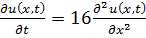 , 0 , 0 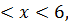  u(x,t) u(x,t) 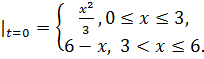 u(x,t) u(x,t)  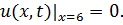 | 8.24. 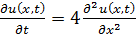 , 0 , 0 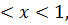  u(x,t) u(x,t) 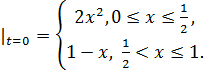 u(x,t) u(x,t)  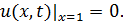 |
8.25. 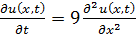 , 0 , 0 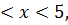  u(x,t) u(x,t) 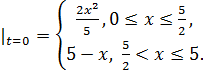 u(x,t) u(x,t)  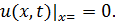 | 8.26. 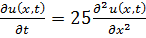 , 0 , 0 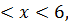  u(x,t) u(x,t) 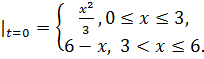 u(x,t) u(x,t)  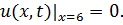 |
8.27. 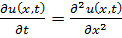 , 0 , 0 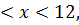  u(x,t) u(x,t)  u(x,t) u(x,t)  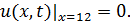 | 8.28. 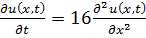 , 0 , 0 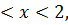  u(x,t) u(x,t) 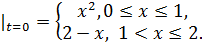 u(x,t) u(x,t)  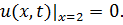 |
8.29. 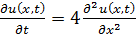 , 0 , 0 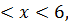  u(x,t) u(x,t) 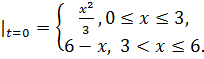 u(x,t) u(x,t)  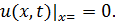 | 8.30. 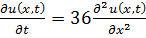 , 0 , 0 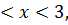  u(x,t) u(x,t) 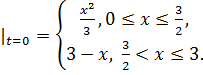 u(x,t) u(x,t)  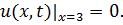 |
Указания к решению расчетно-графической работы №1:
1. Смешанная задача для уравнения теплопроводности с неоднородными граничными условиями u(0,t)=A(t), u(q,t)=B(t) сводится к задаче с однородными граничными условиями с помощью замены u(x,t)= v(x,t)+A(t)+
2. Смешанная задача для неоднородного уравнения теплопроводности сводится к смешанной задаче для однородного уравнения теплопроводности с помощью подбора частного решения методом неопределенных коэффициентов.
Расчетно-графическая работа №2 «Специальные функции, интегральные преобразования и их применение»
Теоретические вопросы
1. Преобразование Лапласа. Оригиналы и изображения.
2. Теоремы линейности, подобия, смещения, запаздывания.
3. Теоремы дифференцирования и интегрирования оригиналов и изображений.
4. Свёртка функций. Теорема умножения.
5. Теорема обращения. Нахождение оригинала по известному изображению.
6. Применение преобразования Лапласа при решении дифференциальных уравнений.
Задания для расчетно-графической работы №2 «Специальные функции, интегральные преобразования и их применение»
Задание 1. Найти решение первой смешанной задачи для стационарного уравнения теплопроводности в круге Δu(r,φ)=0, где Δu(r,φ)= 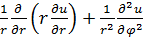
1.1. 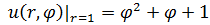 , 0 , 0 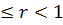 . . | 1.2. 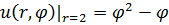 , 0 , 0 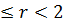 . . |
1.3. 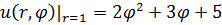 , 0 , 0  1. 1. | 1.4. 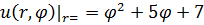 , 0 , 0 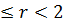 . . |
1.5. 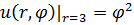 , 0 , 0 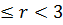 . . | 1.6. 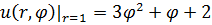 , 0 , 0 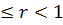 . . |
1.7. 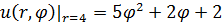 , 0 , 0  . . | 1.8.  , 0 , 0 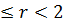 . . |
1.9. 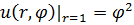 , 0 , 0 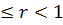 . . | 1.10. 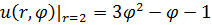 , 0 , 0 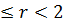 . . |
1.11. 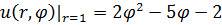 , 0 , 0  1. 1. | 1.12. 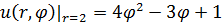 , 0 , 0  2. 2. |
1.13. 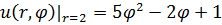 , 0 , 0  2. 2. | 1.14. 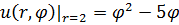 , 0 , 0  2. 2. |
1.15. 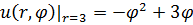 , 0 , 0  3. 3. | 1.16. 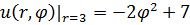 , 0 , 0  3. 3. |
1.17. 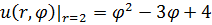 , 0 , 0  2. 2. | 1.18. 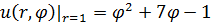 , 0 , 0  1. 1. |
1.19. 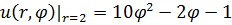 , 0 , 0  2. 2. | 1.20. 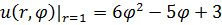 , 0 , 0  1. 1. |
1.21. 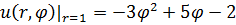 , 0 , 0  1. 1. | 1.22. 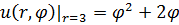 , 0 , 0  3. 3. |
1.23. 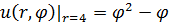 , 0 , 0  4. 4. | 1.24. 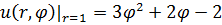 , 0 , 0  1. 1. |
1.25. 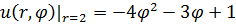 , 0 , 0  2. 2. | 1.26. 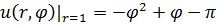 , 0 , 0  1. 1. |
1.27.  , 0 , 0  2. 2. | 1.28. 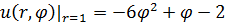 , 0 , 0  1. 1. |
1.29.  , 0 , 0  2. 2. | 1.30. 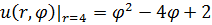 , 0 , 0  4. 4. |
Задание 2.Найти изображение функции, пользуясь теоремами линейности и подобия.
| № | 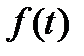 | № | 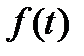 | № | 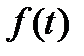 |
| 2.1 | 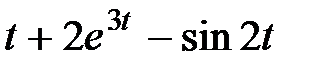 | 2.2 | 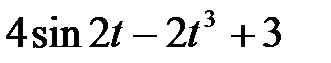 | 2.3 | 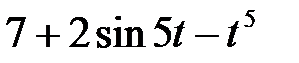 |
| 2.4 | 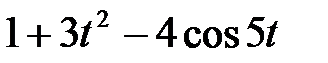 | 2.5 |  | 2.6 | 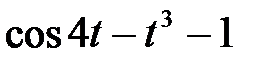 |
| 2.7 | 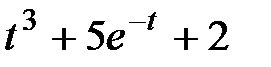 | 2.8 | 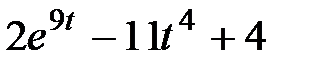 | 2.9 | 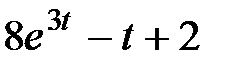 |
| 2.10 | 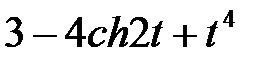 | 2.11 | 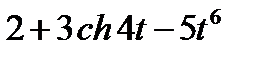 | 2.12 | 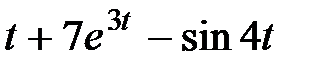 |
| 2.13 |  | 2.14 | 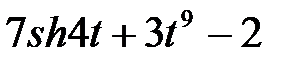 | 2.15 | 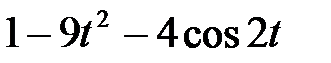 |
| 2.16 | 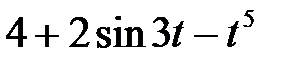 | 2.17 | 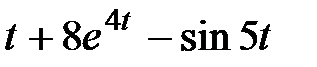 | 2.18 | 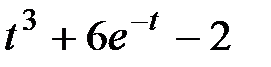 |
| 2.19 | 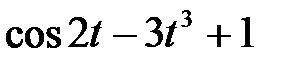 | 2.20 | 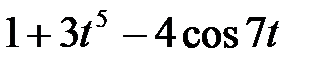 | 2.21 | 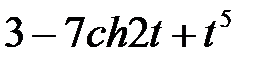 |
| 2.22 | 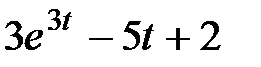 | 2.23 | 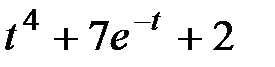 | 2.24 | 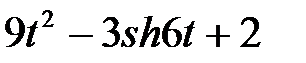 |
| 2.25 | 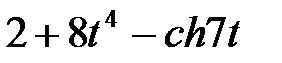 | 2.26 | 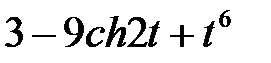 | 2.27 | 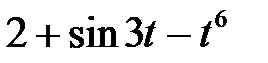 |
| 2.28 | 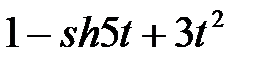 | 2.29 | 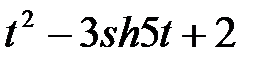 | 2.30 |  |
Задание 3. Найти свёртку функций 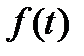
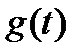
| № | 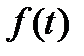 | 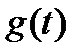 | № | 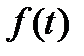 | 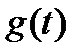 | № | 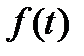 | 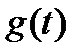 |
| 3.1 | 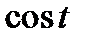 | 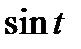 | 3.2 | 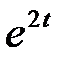 | 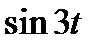 | 3.3 | 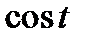 | 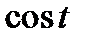 |
| 3.4 | 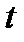 | 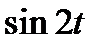 | 3.5 | 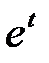 | 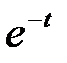 | 3.6 | 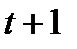 | 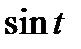 |
| 3.7 | 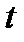 | 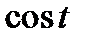 | 3.8 | 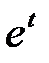 | 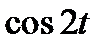 | 3.9 | 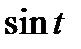 | |
| 3.10 | 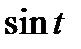 | 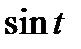 | 3.11 | 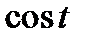 | 3.12 | 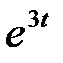 | ||
| 3.13 | 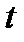 | 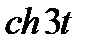 | 3.14 | 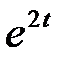 | 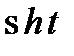 | 3.15 | 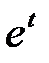 | 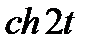 |
| 3.16 | 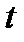 | 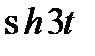 | 3.17 | 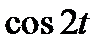 | 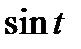 | 3.18 | 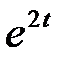 | 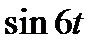 |
| 3.19 | 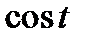 | 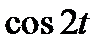 | 3.20 | 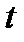 |  | 3.21 | 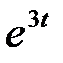 | 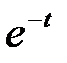 |
| 3.22 | 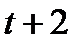 | 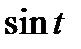 | 3.23 | 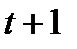 | 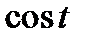 | 3.24 | 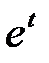 | 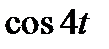 |
| 3.25 | 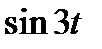 | 3.26 | 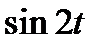 | 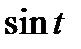 | 3.27 | 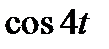 | ||
| 3.28 | 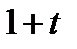 | 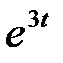 | 3.29 | 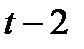 | 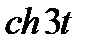 | 3.30 | 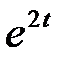 | 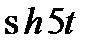 |
Задание 4.Найти оригинал 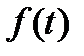
💥 Видео
8.2 Теплопроводность на отрезке. Сложные задачи.Скачать

Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Решение неоднородного уравнения теплопроводностиСкачать

Неоднородное уравнение колебания струныСкачать

Решение уравнения теплопроводности / граничные условия второго и третьего родаСкачать

Стационарное решение одномерного уравнения теплопроводности.Скачать

15. Решение уравнения теплопроводности в кругеСкачать

УМФ, 01.12, решение задач Лапласа и Пуассона в случае неоднородных граничных условийСкачать
Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Разбор решения задачи Штурма-ЛиувилляСкачать

4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

Неоднородное уравнение теплопроводности. Ненулевые граничные условия.Скачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 2)Скачать