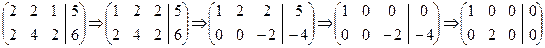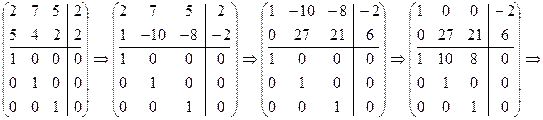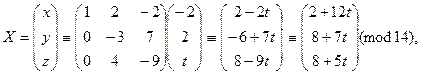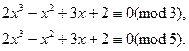Решить систему уравнений в поле вычетов по указанному модулю (3 видео)

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 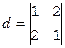, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

В дальнейшем станем действовать аналогично, к тому же не будем педантично ставить индекс +_n, ×_n около символов операций, обозначая их просто + и
× , если значение индекса n ясно из контекста.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре определителя:

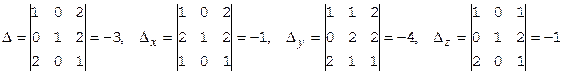
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

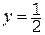
Сделаем проверку (символом Þ обозначен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найденные значения вычетов удовлетворяют системе уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

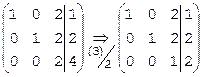
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .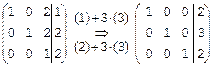

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Видео:Система уравнений с модулями #1Скачать

Системы линейных сравнений по модулю. Китайская теорема об остатках

Определение 1.Системой m линейных cравнений с n неизвестными x₁, x₂,…, x_n (СЛCУ) называется система cравнений вида:

(1)

Определение 2.Решением системы сравнений (1) называется такой вектор , состоящий из классов вычетов по некоторому модулю m, для которого любой вектор целых чисел

удовлетворяет всем сравнениям системы (1).

Рассмотрим сначала случай, когда все модули m₁,…, m_k в системе (1) равны и система (1) имеет вид:

(2)

Если p простое число, то множество классов вычетов Z_p по модулю p является полем и для системы сравнений применимы все методы решений и основные теоремы, которые имеют место для теории СЛУ над полем.

Пример 1.Решить СЛС

Способ 1. Метод Гаусса:

Все операции выполняются по модулю 7 или в роле Z₇.

Способ 2. Правило Крамера:

Тогда система равносильна системе

Ответ: .

В общем случае для решению системы сравнений вида (2) можно применить методы, изложенные в лекции 2 для решения систем линейных диофантовых уравнений, учитывая следующие замечания:

Нельзя умножать или делить сравнения системы на числа, которые не взаимно простые с модулем, так как при этом может получиться не равносильная система сравнений. Такие преобразования системы назовем элементарными целочисленными приведенными преобразованиями.

Определение 3. Целая матрица D = (d_ij) размерности m´n называется матрицей канонического вида, если она обладает свойствами:

Элементы d_ij, i = 1, 2,…,k, где k = min <m, n>, называем диагональными элементами канонической матрицы. Обозначим число ненулевых диагональных элементов канонической матрицы через r. Очевидно, что r = rang D.

Теорема 1.Любую целую матрицу конечным числом целочисленных приведенных элементарных преобразований строк и столбцов можно привести к матрице канонического вида, при этом r = rang A.

Диагональные элементы d₁₁,…, d_rr, r = rang A, матрицы канонического вида, эквивалентной матрице A, называются элементарными делителями матрицы A.

Теорема 2.Система ЛC (2) разрешима тогда и только тогда, когда НОД(d_ii, m), элементарных делителей d_ii матрицы A делит соответствующие элементарные делители расширенной матрицы СЛС.

Пример 2. Выяснить разрешимость данной СЛС

Решение. Приводим матрицу и расширенную матрицу СЛС к каноническому виду.

Так как элементарные делители матриц равны, то данная СЛДУ разрешима.

Алгоритм решения СЛС Пусть дана СЛС (2). Запишем ее в матричном виде:

Расширенную матрицу СЛДУ (2) расширим вторично, приписав к ней снизу единичную матрицу размерности n´n и нулевую матрицу размерности n´1. Получим дважды расширенную матрицу СЛДУ:

Преобразуем матрицу A к каноническому виду D, выполняя элементарные целочисленные приведенные преобразования над первыми m строками и первыми столбцами n матрицы . Тогда матрица B перейдет в матрицу F = U₁B, где U₁ — произведение элементарных матриц, соответствующих элементарным преобразованиям строк. Единичная матрица E¢ перейдет в матрицу U₂, где U₂ — произведение элементарных матриц, соответствующих элементарным преобразованиям столбцов. Получим матрицу:

Полученной матрице соответствует матричное уравнение:

(5)

Если хотя бы один из элементов f_r _{+ 1} ,…, f_m не сравним с нулем по mod m, или хотя бы одно из чисел f_k не делится на D_k =НОД(d_kk, m), (k =1, 2, …, r), то система (5), а поэтому и система (2) не имеют решений. Если же

Так как Y = U₂ -1 X, то отсюда находим

Пример 3. Решить СЛC:

Решение. Составим дважды расширенную матрицу и приведем ее к каноническому виду:

Отсюда приходим к системе сравнений вида (5):

где t Î Z₁₂. Таким образом, получаем решения сравнения:

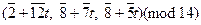
Случай, когда дана СЛУ с различными модулями решается более сложно. Рассмотрим СЛС простейшего вида с одним неизвестным:

(6)

но с различными и попарно взаимно простыми модулями.

Тогда совокупность всех значений x, удовлетворяющих системе (5), определяется сравнением

Доказательство.Для любого j ¹ s все M_j делятся на m_s. Тогда отсюда и из (7) следует, что

Тогда система (6) равносильна системе:

Так как числа m₁,…, m_k – попарно взаимно простые, то система (10) равносильна сравнению (9).ÿ

Из теоремы 3 следует, что для любых попарно взаимно простых целых чисел m₁,…, m_k и любых целых чисел r₁,…, r_k где 0 £ r₁ n + a₁x n — 1 +…+a_n Î Z[x], a₀ T 0(mod p). Рассмотрим сравнение

Так как кольцо классов вычетов Z_p по простому модулю p является полем, то рассматривая сравнение (1) как уравнение над конечным полем Z_p, можем применить к сравнению (1) всю теорию многочленов над конечным полем и получаем следующие теоремы.

Теорема 1.Любое сравнение вида (1) равносильно нулевому сравнению или сравнению степени не большей p-1.

Доказательство.Разделим многочлен f (x) на многочлен x p – x с остатком

где – нулевой многочлен или многочлен степени не выше p-1. Так как по теореме Ферма для любого целого числа a

то сравнение (1) равносильно сравнению

Теорема 2.Число x₀ удовлетворяет сравнению (1) тогда и только тогда, когда

Теорема 3.Если число решений сравнения (1) больше чем n решений, то все его коэффициенты делятся на p.

Доказательство.Допустим, что сравнение (1) имеет, по крайней мере, n + 1 решений. Обозначим числами x₁, x₂, …, x_n₊₁ вычеты этих решений. Деля многочлен f (x) с остатком последовательно на двучлены x — x₁, x — x₂, …, x — x_n представим многочлен f (x) в виде:

Следствие.Если a₀ T 0(mod p), то число решений сравнения (1) не больше степени сравнения.

Доказательство.Допустим, что сравнение (1) имеет более чем n решений, то все его коэффициенты делятся на p. Тогда a₀ º 0(mod p), и получили противоречие с условием.ÿ

Теорема 4(теорема Вильсона).Число p простое, тогда и только тогда, когда справедливо сравнение

Доказательство.Длячисла p = 2 сравнение выполняется. Пусть p – нечетное простое число. Тогда по малой теореме Ферма следует, что сравнение

имеет p -1 решений `0, `1 ,…, `p-1. Тогда по теореме 2 получим:

Отсюда при x º 0(mod p) следует формула (4).ÿ

равносильно системе сравнений

(6)

при этом, число T решений сравнения (5) равно

где T₁,…, T_k – обозначают соответственно число отдельных решений сравнений системы (6).

Доказательство.Первая часть теоремы 1 следует из свойства делимости на взаимно простые числа:число a делится на m тогда и только тогда, когда оно делится на каждый из взаимно простых множителей m₁,…, m_k числа m.

Пусть теперь все попарно различные решения соответственно сравнений системы (6). Тогда для каждого набора чисел ; i=1,…,T₁;…; j=1,…,T_k по формуле (8) предыдущего параграфа находится число, удовлетворяющее всем сравнениям системы (6), т.е. удовлетворяющее системе (5). При этом все полученные числа попарно несравнимы по модулю m. Таким образом система (6) имеет T = T₁… T_k решений.ÿ

Пусть — каноническое разложение числа m. В виду теоремы 5 исследование и решение сравнения

(7)

сводится к исследованию и решению сравнений:

. (8)

Поэтому рассмотрим сравнение вида:

, (9)

где p – простое число. Покажем, что решение этого сравнения сводиться к решению сравнения (1).

Теорема 6.Всякое решение x º x₁ (mod p) сравнения (1) при условии, что f´(x₁) не делится на p, даст одно решение сравнения (9):

(10)

Доказательство.Так как всякое число x, удовлетворяющее сравнению (9) удовлетворяет и сравнению (1), то x º x₁ (mod p), где x₁ – какое-нибудь решение сравнения (1).

Обратно, пусть x₁ – любое решение сравнения (1), x º x₁ (mod p). Тогда x = x₁ + pt₁, где t₁ – целое число. Подставляем это значение x в сравнение

(11)

и применяем формулу Тейлора n-го порядка, получим:

Заметим, что в этой формуле все коэффициенты в формуле целые числа и последние n – 2 членов делятся на p. Тогда сравнение (11) принимает вид:

Так как f´(x₁) не делится на p, то последнее сравнение имеет единственное решение

где t₂ – целое число. Тогда выражение для x принимает вид

где t₂ – целое число. Подставляя это значение x в сравнение

(12)

где t₃ – целое число. Тогда выражение для x принимает вид

Продолжая эти рассуждения, получим справедливость утверждения теоремы.ÿ

Пример 1. Решить сравнение

f(x) = 2x 3 — x 2 + 3x +2 º 0 (mod 225). (13)

Так как 225 = 3 2 5 2 , то сравнение равносильно системе сравнений:

(14)

методом испытаний, выполняя проверку по схеме Горнера:

a	-1
-1	mod 3
mod 3
mod 3
-1	mod 5
mod 5
mod 5
mod 5
mod 5

Первое сравнение имеет 1 решение x º 1(mod 3), второе сравнение имеет 1 решение x º 2(mod 5). Далее

f´ (1) = 7 º 1 T 0(mod 3),

f´ (2) = 24 – 4 + 3 = 23 º 3 T 0(mod 5),

то каждое из сравнений (14) и сравнение (13) имеет по одному решению.

Решая первое из сравнений (14) положим x = 1 + 3t₁, где t₁ – целое число. Подставляем это значение x в сравнение, получим

Решая второе из сравнений (14) положим x = 2 + 5t₁, где t₁ – целое число. Подставляем это значение x в сравнение, получим

Все решения сравнения (13) являются решениями системы сравнений:

M₂´ º 9 19 º 9× (9 2 ) 9 º 9×6× (6 2 ) 4 º 4× (11 2 ) 2 º 4× 4 2 º -4×9 º -11 (mod 25),

Тогда число x₀ вычислим о формуле:

Ответ: .

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгоритм решения систем линейных уравнений в кольцах вычетов

1 Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов [], эквивалентный по сложности известному алгоритму решения систем в полях Галуа ([2], [4]). Приведены результаты сравнительного анализа предложенного алгоритма и существующих аналогов ([3], [0], [8]) на основе асимптотической оценки их временной сложности. Показано, что разработанный метод является корректным и существенно снижает трудоемкость алгоритмов дискретного логарифмирования. Введение Объектом исследования данной работы являются методы решения систем линейных уравнений в кольцах вычетов. Такие системы возникают в алгоритмах факторизации и дискретного логарифмирования (см., например, метод Диксона, алгоритм Копперсмита-Одлыжко-Шреппеля «COS» и алгоритм решета числового поля в [3]). Частным случаем колец вычетов являются поля Галуа, т.е. кольца вычетов по модулю простых чисел. Методы решения систем в таких полях известны (см., например, метод Гаусса (последовательного исключения) в [2, с.89], [4, с.42]). Модификацией метода Гаусса является метод Жордана. Однако для решения систем линейных уравнений в кольцах вычетов эти методы, вообще говоря, неприменимы. Проиллюстрируем сказанное. Рассмотрим систему линейных уравнений: 26x+ 3y = 4 () 9x+ 34y = в поле Галуа Z 37 и в кольце вычетов Z 36. В соответствии с методом Жордана требуется с помощью элементарных преобразований над строками привести матрицу к единичной. Для получения единичного элемента на диагонали в поле действительных чисел используется деление на число a, равное ведущему элементу; аналогом этой операции в кольце вычетов является умножение на элемент, обратный к a. Обратный элемент по модулю можно найти как решение уравнения: ax (mod ) (2) Для его вычисления используется расширенный алгоритм Евклида (см. [7, с. 744], [0, с.227]). На рис. приведено описание этого алгоритма. Если a и — взаимно простые числа, т.е. НОД( a, ) = = ax + y, то 2 ; в противном случае коэффициент Безу x является решением уравнения ( ) уравнение ( ) 2 не имеет решения и элемент a необратим в кольце Z. Как показано в [7, с.743], время работы алгоритма Евклида при вычислении НОД ( ab, ), где a > b 0, составляет O(log b ). Тогда

2 сложность операции вычисления обратного элемента в кольце Z можно оценить как O(log ). Метод Жордана с учетом алгоритма Евклида имеет временную сложность O( n ( n m+ log ) ) для системы n уравнений с m неизвестными в Z. Евклид( ab, ). d x y a 0 n r s b 0 2. c d / n 3. d x y 0 d x y n r s c n r s 4. ЕСЛИ n > 0 5. ТО перейти к шагу 2; 6. ИНАЧЕ вернуть( d, x, y, r, s ) Рис. В результате вычислений, приведенных ниже, получаем решение системы в поле Галуа Z 37 : x = 6, y = 23. [] [] ( 26 = 0 ) 30 3 [2] [] [2] [] 30 3 [2] ( 23 = 29 ) 30 3 [] [2] [2] Однако в кольце вычетов по модулю = 36 система () не может быть решена ни с помощью метода Жордана, ни с помощью метода Гаусса, поскольку все коэффициенты при неизвестных являются делителями нуля ([9, с.75]) и, следовательно, не является обратимыми. Таким образом, получить единичный элемент на диагонали умножением на какой-либо элемент кольца невозможно. Тем не менее, конечность области определения позволяет убедиться в том, что решение данной системы в Z 36 существует ( x = 7, y = 22), и притом единственно. Для решения систем линейных уравнений в кольцах вычетов необходимы специальные методы. Обзор существующих методов Анализ методов решения систем линейных уравнений в кольцах вычетов, описанных в современной литературе, выявил ряд недостатков, которые затрудняют использование этих алгоритмов на практике. В монографии [3] задача сводится к решению систем линейных уравнений над полями Галуа. Пусть

3 где систем t q α = m = ( ) ax b(mod ), i=, n 3 i i =, тогда решение системы ( ) m = 3 сводится к решению семейства ( ) ax b(mod q α ), i=, n, =, t 4 i i где неизвестные значения x (mod q α ) для фиксированного представляются в виде α α x x + x q x q (mod q ), 5 0, α Здесь 0 xl q, l = 0, α. Редуцируя систему ( 4 ) к модулю q, получаем систему уравнений: над полем Галуа виде ( ) q m = 5 с известными i0 поделив на i 0 ax b(mod q), i=, n ( ) Z. Если мы найдем все x,, 0 = m, то, подставляя x в x в систему ( ) 4, редуцируя ее к модулю q, мы получим систему линейных уравнений над полем 2 q и затем относительно неизвестных x,, = m, и т.д. В конечном счете, найдя значение x (mod q α ) для всех, мы восстановим x (mod ) по китайской теореме об остатках (см. [0, с.420]). 2 2 В нашем примере = 36 = 2 3, т.е. для решения одной системы в кольце вычетов придется решить 4 системы над полями Галуа. Но основным недостатком метода является необходимость разложения на множители числа : вопрос о существовании алгоритма факторизации с полиномиальной сложностью является одной из открытых проблем современной теории чисел. Другой метод предполагает сведение системы линейных уравнений в кольце вычетов к системе линейных диофантовых уравнений. При помощи одного из известных алгоритмов (см. [3] или [0]) расширенная матрица системы ( A b ) приводится к ступенчатому виду ( A b ) и вычисляется правая матрица перехода R размером ( m+ ) ( m+ ), такая, что: ( A b) R = ( A b ). На основании матрицы R можно получить общее решение системы. Проиллюстрируем применение данного способа на примере. Система линейных диофантовых уравнений, соответствующая системе ( ) в Z 36, имеет вид: 26x+ 3y+ 36v = 4. 9x+ 34y + 36v2 = Ее общее решение в кольце целых чисел: Z q

4 x = t t (-2492) y = t0 (-324) + t 5688, t0, t Z v = t0 (-857) + t 5048 v2 = 0 + t0 0 + t Редуцируя результат к модулю 36, получаем: x = 7, y = 22. Однако при решении систем линейных уравнений в кольцах вычетов наблюдается экспоненциальный рост длины коэффициентов. Так, в нашем примере коэффициенты исходной матрицы ограничены числом 36, тогда как в 6 целых числах мы получили общее решение с коэффициентами

0. Заметим, что этот результат соответствует системе в кольце вычетов, состоящей всего лишь из двух уравнений с двумя неизвестными. Для того, чтобы избежать экспоненциального роста длины коэффициентов, разработаны специальные методы решения систем линейных алгебраических уравнений над кольцом целых чисел, такие как модификация метода Гаусса и построение нормальной диагональной формы Смита (см. [8, с. 8]). Несмотря на то, что эти алгоритмы являются полиномиальными, их сложность существенно превышает сложность алгоритма Гаусса при решении систем в полях Галуа. Так, для системы из n уравнений с n неизвестными, коэффициенты которой по абсолютной величине не превосходят α, временная сложность модифицированного алгоритма Гаусса при использовании самого быстрого алгоритма умножения составляет O( n 4 (log α + log n ) ). Трудоемкость построения нормальной диагональной формы Смита матрицы 2 O n m 2 logα. A, где a α, i, n,, m n m i = =, ограничена величиной ( ) Метод решения систем линейных уравнений в кольцах вычетов, предлагаемый в данной работе, лишен недостатков вышеописанных алгоритмов и показал свою эффективность при программной реализации. Описание метода В основе разработанного метода лежит преобразование строк матрицы с использованием коэффициентов Безу, которые позволяет вычислить расширенный алгоритм Евклида (см. рис.). В результате работы алгоритма получаем: НОД ( ab, ) = d= a x+ b y, 0 = n = a r+ b s. a = 26 = a, b= 9 = a : НОД (26, 9) = = 26 ( ) + 9 (3), 0= 26 (9) + 9 ( 26). При 2 Применяя к -й и 2-й строке расширенной матрицы системы () преобразования, соответствующие преобразованиям алгоритма Евклида над поступающими на его вход коэффициентами a = 26 и a 2 = 9, в результате мы получаем матрицу, строчно эквивалентную исходной (см. [5, с.27]):

5 [] [] [2] [] [2] 9 34 [2] [] 9 34 [] [2] [] [2] [2] [] [] [2] [] [2] [2] В полученной матрице: A(, ) x y A(, ) = A(2, ) r s A(2, ), где x, y, r, s удовлетворяют условию: НОД ( a, a2) = a x + a2 y, 0 = a r + a2 s (запись A(, ) используется для обозначения -й строки расширенной матрицы A). Коэффициенты Безу x =, y = 3, r = 9, s = 26 можно получить, оперируя лишь коэффициентами a и a 2. Тогда цепь преобразований ( 6 ) сводится к одному преобразованию следующего вида: [] [] =[] 35 + [2] [2] =[] 9 + [2] 0 [2] С учетом того, что коэффициент a 22 = 7 обратим в Z 36 : 7 3(mod36), преобразуем матрицу к единичной и получаем решение: [] [] =[] + [2] [2] =[2] 3 [2] В общем виде алгоритм решения систем линейных уравнений в кольцах вычетов, представляющий собой модификацию метода Жордана, описан на рис.2. Доказательство корректности Предложенный алгоритм является корректным, т.е. полученная в результате преобразований система равносильна исходной (иначе говоря, решения системы не теряются и новые решения не появляются). 3 в матричном виде: Запишем систему уравнений ( ) Ax = b ( 7) Тогда по теореме о равносильности систем линейных уравнений: Если U — обратимая ( n n) коммутативное кольцо с единицей), тогда система уравнений ( ) системе ( UA) x = Ub. (Доказательство см. в [5, с.58]). Следствие из этой теоремы: ( 6) -матрица над R (R — произвольное 7 равносильна Если матрицы ( A, b ) и ( C, δ ) строчно эквивалентны, то система уравнений ( 7 ) равносильна системе Cx = δ.

6 Поскольку преобразования матрицы в описанном модифицированном методе Жордана базируются на элементарных преобразованиях строк (элементарными преобразованиями строк матрицы с элементами из коммутативного кольца с единицей называют (см. [6, с.85]) умножение любой ее строки на обратимый элемент кольца; прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца; транспозицию строк), то полученная на выходе алгоритма матрица строчно эквивалентна исходной (см. Модиф _ Жордан( A ). n Число _ Строк( A) 2. i 3. ДЛЯ = i+, n ЦИКЛ 4. НОД ( aii, ai ) = aii x + ai y ВЫЧИСЛИТЬ x, y, r, s : 0 = aii r + ai s 5. Ai (, ) x y Ai (, ) A(, ) r s A(, ) 6. ЕСЛИ коэффициент a ii необратим в Z 7. ТО выйти из алгоритма 8. ИНАЧЕ 9. A(, i ) A(, i ) a ii 0. A(, ) A(, ) A( i, ) ai, =, i. i i+ 2. ЕСЛИ i n 3. ТО перейти к шагу 2; 4. ИНАЧЕ вернуть( A) [5, с.27]). Тогда приведенному выше следствию соответствующие системы уравнений являются равносильными. Что и требовалось доказать. Оценка сложности Предложенный алгоритм обладает временной сложностью ( ( log )) Рис.2 O n nm+ для системы в кольце вычетов по модулю, в которой n — число уравнений системы, m — число неизвестных. Для получения этой формулы воспользуемся оценкой временной b сложности алгоритма Евклида T( a, b) = O + logϕ НОД ( a, b), где a > b 0, ϕ = ( + 5) 2 (доказательство этой оценки предлагается в [7, с.745], в качестве упражнения). На каждом -м шаге процедура, реализующая алгоритм Евклида, вызывается раз: первым параметром является текущее значение ведущего

7 элемента, в качестве второго на вход последовательно подаются ai ( i = +, n) и. Пусть di — значение ведущего элемента на i -й итерации цикла: d0 = a, d = НОД ( a, a+, ) = НОД ( d0, a+, ). d = НОД ( d, a ). d = НОД ( d, a ). +, n n n, Тогда число операций оценивается неравенством: n min, + log ( n ) + log НОД ( d, a ). i= i i, Помимо этого, на каждом -м шаге над элементами матрицы производится порядка 2( n )( m+ ) 2nm операций. Число шагов алгоритма для системы равно n. Получаем временную сложность алгоритма: n ( ) ( ). Tn (, ) = 2 nm+ ( n ) + log On ( nm+ log ) = Заключение В заключение приведем сравнительный анализ временной сложности предложенного алгоритма и алгоритмов, описанных в современной литературе, для системы n уравнений с m неизвестными в кольце вычетов Z ( t q α = = ). Алгоритм Модифицированный метод Жордана Метод сведения к полям Галуа* Метод сведения к диофантовым уравнениям (с построением матрицы Смита) Временная сложность ( ( + log )) O n nm t O n ( n m α + log ) + ln lnln e = 2 O n m 2 log р ( ) ln ln ln *Оценка временной сложности этого метода дана при условии использования для разложения на множители числа наиболее эффективного на сегодняшний день (см. [7, c.779]) алгоритма «квадратичного решета» () Померанца, имеющего временную сложность L ( ) + o ln ln ln, где L ( ) e =.

8 Список литературы. Авдошин С.М., Савельева А.А. Свидетельство об официальной регистрации программы для ЭВМ : «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ Ван дер Варден Б.Л. Алгебра. — М.: Наука, с. 3. Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, с. 4. Гантмахер Ф.Р. Теория матриц. Гостехиздат, с. 5. Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра: Учебник. В 2-х т. Т. I — М.: Гелиос АРВ, с. 6. Джекобсон Н. Теория колец (Перевод с английского Н. Я. Виленкина). М.: Государственное издательство иностранной литературы, с. 7. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦНМО, с. 8. Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. Нижегородский Государственный Университет им. Н.И. Лобачевского. htt:// с. 9. Курош А.Г. Теория групп (Издание третье, дополненное). М.: «НАУКА», Главная редакция физико-математической литературы, с. 0. Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. — М.: Мир, с.