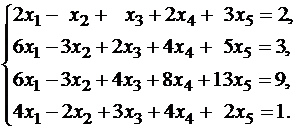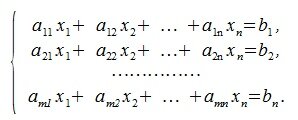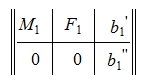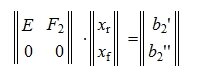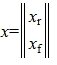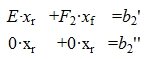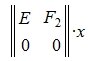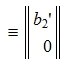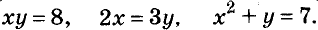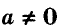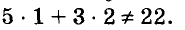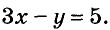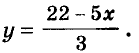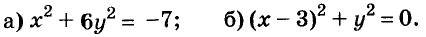Пример 2. Исследовать совместность, найти общее и одно частное решение системы
Решение. Переставим первое и второе уравнения, чтобы иметь единицу в первом уравнении и запишем матрицу B.
Получим нули в четвертом столбце, оперируя первой строкой:
Теперь получим нули в третьем столбце с помощью второй строки:

Третью строку умножим на (–2) и прибавим к четвертой:
Видим, что ранги основной и расширенной матриц равны 4, причем ранг совпадает с числом неизвестных, следовательно, система имеет единственное решение:
-x1=-3 → x1=3; x2=3-x1 → x2=0; x3=1-2x1 → x3=5.
x4 = 10- 3x1 – 3x2 – 2x3 = 11.
Пример 3. Исследовать систему на совместность и найти решение, если оно существует.
Решение. Составляем расширенную матрицу системы.

Умножая первую строку на (-1), складываем ее с третьей:
Умножим вторую строку на (-2) и прибавим к третьей:
Система несовместна, так как в основной матрице получили строку, состоящую из нулей, которая вычеркивается при нахождении ранга, а в расширенной матрице последняя строка останется, то есть rB > rA.
Задание. Исследовать данную систему уравнений на совместность и решить ее средствами матричного исчисления.
Решение
Пример. Доказать совместимость системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) методом Крамера. (ответ ввести в виде: x1,x2,x3)
Решение:doc:doc:xls
Ответ: 2,-1,3.
Пример. Дана система линейных уравнений. Доказать ее совместность. Найти общее решение системы и одно частное решение.
Решение
Ответ:x3 = — 1 + x4 + x5; x2 = 1 — x4; x1 = 2 + x4 — 3x5
Задание. Найти общее и частное решения каждой системы.
Решение. Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:
| 1 | 1 | 14 | 0 | 2 | 0 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
| x1 | x2 | x3 | x4 | x5 |
Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (3). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 3 | 4 | 2 | 3 | 0 | 1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (2). Умножим 3-ую строку на (-3). Добавим 3-ую строку к 2-ой:
| 0 | -1 | 40 | -3 | 6 | -1 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -3 | 6 | -1 |
| 2 | 3 | -3 | 3 | -2 | 1 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4,x5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 0 | 27 | 0 | 0 | 0 |
| 0 | -1 | 13 | -1 | 3 | -6 |
| 2 | 3 | -3 | 1 | -3 | 2 |
| x1 | x2 | x3 | x4 | x5 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
27x3 =
— x2 + 13x3 = — 1 + 3x4 — 6x5
2x1 + 3x2 — 3x3 = 1 — 3x4 + 2x5
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4,x5, то есть нашли общее решение:
x3 = 0
x2 = 1 — 3x4 + 6x5
x1 = — 1 + 3x4 — 8x5
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.
Задание. Решить систему уравнений.
Ответ😡2 = 2 — 1.67x3 + 0.67x4
x1 = 5 — 3.67x3 + 0.67x4
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной
Пример. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера — Капелли. Согласно теореме Кронекера — Капелли, из того, что следует несовместность исходной системы.
Ответ: система не совместна.
Решение
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Система линейных уравнений. Общее решение
Система линейных уравнений (СЛУ) может быть записана в виде
где m, n натуральные числа, aij (i= 1,2, . m, j= 1,2. n) называются коэффициентами, bi (i= 1,2. m) называются свободными членами, xi (i= 1,2. n) называются неизвестными.
Систему линейных уравнений (1) можно записать в виде
где A матрица порядка m×n , x — вектор порядка n (x∈R n ), b — вектор порядка m (b ∈R m ).
Решением системы (2) называется выбор такого вектора x’, что выполнено равенство
Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.
Если СЛУ не имеет решения, то СЛУ называется несовместным.
Если СЛУ имеет единственное решение, то СЛУ называется определенным.
Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.
Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.
Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.
Видео:Решение систем уравнений методом подстановкиСкачать

Нахождение общего решения системы линейных уравнений
Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.
Пусть A m×n — матрица rankA=r. В общем случае можем предположить что r 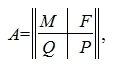
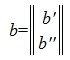
Применяя метод исключения Гаусса для системы (3), получим:
где M1 верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:
где E — единичная матрица порядка r×r.
Запишем (5) в виде системы линейных уравнений:
где
Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:
Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b2»≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора xr:
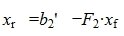 | (8) |
Таким образом первые r координаты вектора x 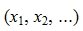
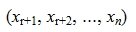
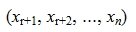
Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).
Рассмотрим множество всех векторов х, удовлетворяющих условию
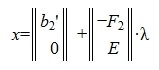 | (9) |
где λ — произвольный вектор-столбец длины n-r.
Подставляя (9) в (6) получим:
Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор 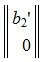
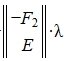
Видео:Матричный метод решения систем уравненийСкачать

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы
Обозначим через R(A) пространство столбцов матрицы A, т.е.
1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A -1 , и следовательно единственное решение СЛУ (2) примет вид:
Действительно, подставляя (3) в (2) имеем:
2. Пусть A m×n − матрица, rank(A)=r.
Видео:Решение систем уравнений. Методом подстановки. Выразить YСкачать

Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
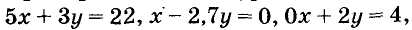
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 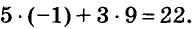
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 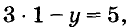
Уравнение 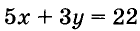
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 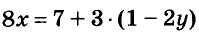
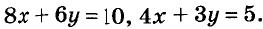
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 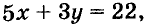
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 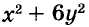
б) Значение выражения 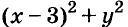
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 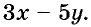
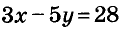
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 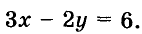
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎬 Видео
Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

6 способов в одном видеоСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Решение системы уравнений методом ГауссаСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Решение системы уравнений методом обратной матрицы.Скачать

Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать
Решение систем уравнений второго порядка. 8 класс.Скачать

Решение системы уравнений методом Крамера.Скачать

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Решение матричных уравненийСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать