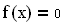Решить систему уравнений используя функцию find (5 видео)

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Содержание

Использование метода Given — Find:
Использование метода Solve:
Решение систем уравнений с помощью функции Find
Решение уравнений с помощью функции Find(x)
🎬 Видео

Видео:MathCAD Решение системы уравненийСкачать

Использование метода Given — Find:

В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

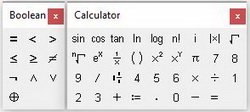
Рис. 1. Ввод исходных данных в поле mathcad

Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Видео:MathCAD. Given - FindСкачать

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

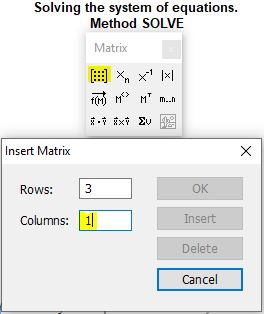
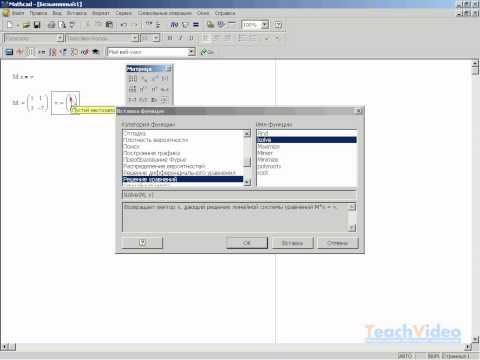
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

Видео:Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать

Решение систем уравнений с помощью функции Find

Дата добавления: 2015-07-23 ; просмотров: 2571 ; Нарушение авторских прав

Лабораторная работа №4

Тема: Решение систем линейных алгебраических уравнений точными методами в MathCAD.

Цель работы: изучение приемов численного и символьного решения систем линейных уравнений с помощью функций MathCAD.

Порядок выполнения работы

1. Ознакомиться с теоретическими положениями.

2. Выполнить практическое задание.

3. Ответить на контрольные вопросы.

Содержание отчета

1. Тема, цель работы.

2. Практическое задание:

2.1. Постановка задачи.

2.2. Результаты выполнения.

3. Ответы на контрольные вопросы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Точные методы – это методы, представляющие собой конечные алгоритмы для вычисления корней системы. К ним относятся матричный способ решения СЛАУ, метод Крамера, метод Гаусса и др.

Решение систем уравнений с помощью функции Find

MathCAD дает возможность решать системы уравнений, содержащих максимальное число уравнений и переменных равное 50. Результатом решения системы будет численное значение искомого корня.

Для решения системы уравнений необходимо выполнить следующее:

— Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.

— Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.

— Ввести уравнения и неравенства в любом порядке. Использовать [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов , ³ и £.

— Ввести любое выражение, которое включает функцию Find, например: а:= Find(х, у).

Возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое–либо выражение, содержащее функцию Find, называют блоком решения уравнений.

Следующие выражения недопустимы внутри блока решения:

— Ограничения со знаком ¹.

— Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.

— Неравенства вида a

\|	следующая лекция ==>
Формула	\|	Решение системы линейных уравнений матричным способом

Не нашли то, что искали? Google вам в помощь!

Видео:Решение СЛАУ в пакете MathCadСкачать

Решение уравнений с помощью функции Find(x)

6.3 Решение уравнений с помощью функции Find(x)

Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Если задано уравнение f(x) = 0, то его можно решить следующим образом с помощью блока Given – Find:

– задать начальное приближение

– ввести служебное слово

– записать уравнение, используя знак жирное равно

– написать функцию find с неизвестной переменной в качестве параметра

В результате после знака равно выведется найденный корень.

Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.

Пример. Решение уравнения 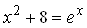с помощью функции find представлено на рисунке 3.3.

Рис. 3.3. Решение уравнения с помощью функции find

Иногда возникает необходимость отметить на графике какие-либо точки (например, точки пересечения функции с осью Ox). Для этого необходимо:

· указать значение x данной точки (по оси Ох) и значение функции в этой точке (по оси Оy);

· дважды щелкнуть по графику и в окне форматирования во вкладке Traces для соответствующей линии выбрать тип графика — points, толщину линии — 2 или 3.

Пример. На графике отмечена точка пересечения функции 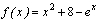с осью Ох. Координата х этой точки была найдена в предыдущем примере: х = 2.742 (корень уравнения ) (рис. 3.4).

Рис. 3.4. График функции 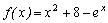с отмеченной точкой пересечения

В окне форматирования графика во вкладке Traces для trace2 изменены: тип графика — points, толщина линии — 3, цвет — черный.

7. Решение систем уравнений 7.1 Решение систем линейных уравнений

Систему линейных уравнений можно решить матричным методом (или через обратную матрицу или используя функцию lsolve(A,B)) и с использованием двух функций Find и функции Minerr.

Пример. Дана система уравнений:

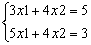
Решение данной системы уравнений матричным методом представлено на рисунке 4.1.

Рис. 4.1. Решение системы линейных уравнений матричным методом

Использование функции lsolve(A,B)

Lsolve(A,B) — это встроенная функция, которая возвращает вектор Х для системы линейных уравнений 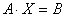при заданной матрице коэффициентов А и векторе свободных членов В.

Пример. Дана система уравнений:

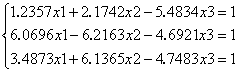
Способ решения данной системы с использованием функции lsolve(A,B) приведен на рисунке 4.2.

Рис. 4.2. Решение системы линейных уравнений с использованием функции lsolve

Решение системы линейных уравнений с помощью функции Find

При данном методе уравнения вводятся без использования матриц, т.е. в «натуральном виде». Предварительно необходимо указать начальные приближения неизвестных переменных. Это могут быть любые числа, входящие в область определения. Часто за них принимают столбец свободных членов.

Для того чтобы решить систему линейных уравнений с помощью вычислительного блока Given – Find, необходимо:

1) задать начальные приближения для всех переменных;

2) ввести служебное слово Given;

3) записать систему уравнений, используя знак жирное равно(=);

4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.

В результате расчетов выведется вектор решения системы.

Пример. Дана система уравнений:

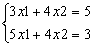
Решение данной системы с помощью вычислительного блока Given – Find приведено на рисунке 4.3.

Рис. 4.3. Решение системы линейных уравнений с помощью функции Find

Приближенное решение системы линейных уравнений

Решение системы линейных уравнений с помощью функцию Minerr аналогично решению с помощью функции Find (используется тот же алгоритм), только функция Find дает точное решение, а Minerr — приближенное. Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке.

Общие рекомендации по решению уравнений и систем уравнений

Ниже перечислены некоторые рекомендации, которые следует выполнять, если MathCAD не может самостоятельно найти решение.

· Можно подобрать другое начальное приближение.

· Можно увеличить или уменьшить точность расчетов. Для этого в меню выбрать Math ► Options (Математика – Опции), вкладка Built-In Variables (Встроенные переменные). В открывшейся вкладке необходимо уменьшить допустимую погрешность вычислений (Convergence Tolerance (TOL)). По умолчанию TOL = 0.001.

Внимание. При матричном методе решения необходимо переставить коэффициенты согласно возрастанию неизвестных х1,х2, х3, х4.

7.2 Решение систем нелинейных уравнений

Системы нелинейных уравнений в MathCAD решаются с помощью вычислительного блока Given – Find.

Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.

Для решения системы уравнений с помощью блока Given – Find необходимо:

1) задать начальные приближения для всех переменных;

2) ввести служебное слово Given;

3) записать систему уравнений, используя знак жирное равно(=);

4) написать функцию Find, перечислив неизвестные переменные в качестве параметров функции.

В результате расчетов выведется вектор решения системы.

Если система имеет несколько решений, алгоритм следует повторить с другими начальными приближениями.

Примечание. Если решается система из двух уравнений с двумя неизвестными, перед решением желательно построить графики функций, чтобы проверить, есть ли корни у системы (пересекаются ли графики заданных функций), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.

Пример. Дана система уравнений

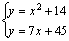
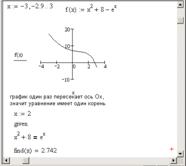
Перед решением системы построим графики функций: параболы (первое уравнение) и прямой (второе уравнение). Построение графика прямой и параболы в одной системе координат приведено на рисунке 4.5:

Рис. 4.5. Построение графика двух функций в одной системе координат

Прямая и парабола пересекаются в двух точках, значит, система имеет два решения. По графику выбираем начальные приближения неизвестных x и y для каждого решения. Нахождение корней системы уравнений представлено на рисунке 4.6.

Рис. 4.6. Нахождение корней системы нелинейных уравнений

Для того чтобы отметить на графике точки пересечения параболы и прямой, координаты точек, найденные при решении системы, введем по оси Ох (значения х) и по оси Оу (значения у) через запятую. В окне форматирования графика во вкладке Traces для trace3 и trace4 изменим: тип графика — points, толщина линии — 3, цвет — черный (рис. 4.7).

Рис. 4.7. Графики функций с отмеченными точками пересечения

8. Примеры использования основных возможностей MathCAD для решения некоторых математических задач

В данном разделе приведены примеры решения задач, для решения которых необходимо решить уравнение или систему уравнений.

8.1 Нахождение локальных экстремумов функций

Необходимое условие экстремума (максимума и/или минимума) непрерывной функции формулируется так: экстремумы могут иметь место только в тех точках, где производная или равна нулю, или не существует (в частности, обращается в бесконечность). Для нахождения экстремумов непрерывной функции сначала находят точки, удовлетворяющие необходимому условию, то есть находят все действительные корни уравнения .

Если построен график функции, то можно сразу увидеть — максимум или минимум достигается в данной точке х. Если графика нет, то каждый из найденных корней исследуют одним из способов.

1-й способ. Сравнение знаков производной. Определяют знак производной 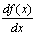в окрестности точки (в точках, отстоящих от экстремума функции по разные стороны на небольших расстояниях). Если знак производной при этом меняется от «+» к «–», то в данной точке функция имеет максимум. Если знак меняется от «–» к «+» , то в данной точке функция имеет минимум. Если знак производной не меняется, то экстремумов не существует.

2-й способ. Вычисление второй производной. В этом случае вычисляется вторая производная 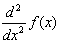в точке экстремума. Если она меньше нуля, то в данной точке функция имеет максимум, если она больше нуля, то минимум.

Пример. Нахождение экстремумов (минимумов/максимумов) функции .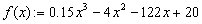

Сначала построим график функции (рис. 6.1).

Рис. 6.1. Построение графика функции

Определим по графику начальные приближения значений х, соответствующих локальным экстремумам функции f(x). Найдем эти экстремумы, решив уравнение 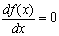. Для решения используем блок Given – Find (рис. 6.2.).

Рис. 6.2. Нахождение локальных экстремумов

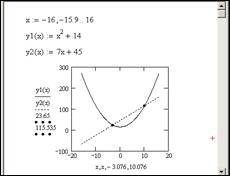
Определим вид экстремумов первым способом, исследуя изменение знака производной в окрестности найденных значений (рис. 6.3).

Рис. 6.3. Определение вида экстремума

Из таблицы значений производной и из графика видно, что знак производной в окрестности точки x1 меняется с плюса на минус, поэтому в этой точке функция достигает максимума. А в окрестности точки x2 знак производной поменялся с минуса на плюс, поэтому в этой точке функция достигает минимума.

Определим вид экстремумов вторым способом, вычисляя знак второй производной (рис. 6.4).

Рис. 6.4. Определение вида экстремума с помощью второй производной

Видно, что в точке x1 вторая производная меньше нуля, значит, точка х1 соответствует максимуму функции. А в точке x2 вторая производная больше нуля, значит, точка х2 соответствует минимуму функции.