Решить систему линейных уравнений над полем

Видео:Неоднородная система линейных уравненийСкачать

Системы линейных уравнений над полем.

Рассмотрим один из наиболее распространенных на практике методов решения систем линейных уравнений над полем_; называемый методом Гаусса.

Пусть дана система уравнений над произвольным полем. Если А = Оmхn, то система совместна только при β ↓ = 0 ↓ . При выполнении этого условия любой вектор из Р ( n ) является ее решением. Далее считаем, что А — ненулевая матрица. Приведем расширенную матрицу В = (А,β ↓ ) к специальному ступенчатому виду с помощью элементарных преобразований строк. Пусть при этом получилась матрица С = (с_ij)_mx(n+1)типа S(i₁. i_r). Тогда система равносильна системе уравнений

где С’ = (с_ij)_mхn,a γ ↓ —последний столбец матрицы С. В зависимости от значений параметров r,i₁. i_r возможны следующие три принци­пиально различных случая.

1) i_r = п + 1. В этом случае столбец β ↓ матрицы В не выражается линейно через столбцы матрицы А, и система уравнений несовместна.

2) i_r ≤ n,r= п.В этом случае матрица С имеет тип S(1,2. n), а тогда имеем:β ↓ = A₁ ↓ c_{1 n+1} + . + A_n ↓ c_nn+1 и система столбцов A₁ ↓ , . , A_n ↓ линейно независима. Отсюда и следует, что столбецγ ↓ является единственным решением системы уравнений . Следовательно, в рассматриваемом случае система совместна и определенна.

которая, очевидно, равносильна системе (1), Подставляя в (3) вместо х_ir+1. x_iппроизвольные элементы air+l , . , a_inполя P, мы однозначно определим значения а_i1. а_ir остальных неизвестных x_i1. x_ir так, что набор (a₁. ,a_n) будет решением системы (3). Нетрудно заметить, что каждое решение системы (3) можно получить указанным способом. Так как r ↓ ), можно сделать следующий вывод. При решении системы уравнений методом Гаусса логически возможны следующие взаимно исключающие случаи:

1) rangA ≠rangВ, система несовместна;

2) rangА = rangВ= п, система совместна и определенна;

Эту теорему называют теоремой Кронекера-Капеллив честь немецкого математика Л. Кронекера (1823—1891) и итальянского математика А. Капелли (1855-1910).

Пояснение. Система уравнений Ax=b разрешима тогда и только тогда, когда operatorname A = operatorname(A, b), где (A, b) — расширенная матрица, полученная из матрицы A приписыванием столбца b.

ДОК-ВО

Пусть система совместна. Тогда существуют числа x_1,dots,x_ninmathbb R такие, что b=x_1 a_1+dots+x_n a_n. Следовательно, столбец b является линейной комбинацией столбцов a_1,dots,a_n матрицы A. Из того что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что operatorname A = operatorname B.

Пусть operatorname A = operatorname B = r. Возьмём в матрице A какой-нибудь базисный минор. Так как operatorname B = r, то он же будет базисным минором и матрицы B. Тогда, согласно теореме о базисном миноре, последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Следствия

· Количество главных переменных системы равно рангу системы.

· Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Теорема (критерий определенности).Система линейных уравнении над полем имеет единственное решение тогда и только тогда,когда ранги основной и расширенной матриц системы равны числу её неизвестных.

Теорема.Совместная и неопределенная система линейных уравнений над полем Р имеет бесконечно много решений при бесконечном поле Р и q n — r решений при |Р| = q, где п — число неизвестных, аr — ранг основной (и расширенной) матрицы системы.

Рассмотрим еще метод решения систем линейных уравнений над полем, основанный на использовании ранговых подматриц матриц этих систем.

Пусть дана система с основной матрицей А и расширенной матрицей В = (A, β ↓ )и известно, что rangA = rangВ = r. Выберем в матрице А произвольную ранговую подматрицу

Так как rangB = r и А есть подматрица матрицы В, то А’ является ранговой подматрицей и для матрицы В, Отсюда и легко получить, что система строк является базисом системы всех строк матрицы В. Поэтому матрицу В элементарными преобразованиями строк можно привести к матрице вида:

Также равносильна системе уравнений

где β‘ ↓ — последний столбец матрицы B’, а А’ получена из В’ удалением столбца β‘ ↓ . Удалив из системы (4) последние m-r уравнений и перенеся в оставшихся уравнениях в правые части все слагаемые, не содержащие неизвестных x_j1, . , x_jrполучим систему из r уравнений, равносильную системе:

(5)

Подставив в (5) вместо x_jr+1, . , x_jnпроизвольные элементы из Р, мы получим систему rуравнений с r неизвестными x_j1, . x_jr, которая по теореме Крамера имеет единственное решение x_j1= a_j1, . x_jr= а_jr. В итоге мы найдем решение (a₁, . a_n) системы (5) . Легко видеть, что таким образом можно получить все решения системы (5). Действительно, если γ = (с₁, . ,c_n) — любое решение системы (5), то, заменив в (5) х_i на с_i при всех i Є 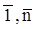,получим систему верных равенств, которая свидетельствует о том, что c_j1. c_jrесть решение системы, полученной из (5) заменой x_jr+1, . x_jnсоответственно элементами c_jr+1. c_jn.

Замечание 1. Вместо того чтобы решать методом Крамера все системы уравнений, получаемые из (5) заменой xjr+1, . , xjn всевозможными элементами поля Р, можно решить методом Крамера саму систему (5), считаяx_jr+1. x_jn параметрами со значениями из поля Р. В итоге неизвестные x_j1, . , x_jrбудут представлены в виде аффинных функций от переменных x_jr+1, . , x_jn. Придавая последним произвольные значения из Р и вычисляя соответствующие значения неизвестных x_j1. x_jrполучим все решения системы (5).

Замечание 2. Набор неизвестных x_jr+1, . x_jnиз правых частей уравнений системы (5) называют системой свободных неизвестных системы уравнений В общем случае система свободных неизвестных для системы находится неоднозначно, а определяется выбором ранговой подматрицы в матрице A.

3. Поле частных коммутативного кольца без делителей нуля. Простые поля. Расширения полей. Поле разложения многочлена. Конечные поля и их свойства

По́ле в общей алгебре — алгебра, для элементов которой определены операции сложения, вычитания, умножения и деления (кроме деления на нуль), причём свойства этих операций близки к свойствам обычных числовых операций. Простейшим полем является поле рациональных чисел (дробей). Хотя названия операций поля взяты из арифметики, следует иметь в виду, что элементы поля не обязательно являются числами, и определения операций могут быть далеки от арифметических.

По́лем называется множество F с двумя бинарными операциями + (аддитивная операция или сложение) и cdot (мультипликативная операция или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей, все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями + (сложение) и cdot (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.

Примеры полей

Числа вида a + bsqrt, a,bin , относительно обычных операций сложения и умножения. Это один из примеров квадратичного поля, которое образует подполе в .

_p — поле вычетов по модулю p, где p — простое число.

_q — конечное поле из q=p^k элементов, где p — простое число, k — натуральное. Все конечные поля имеют такой вид.

(x) — поле рациональных функций вида f(x)/g(x), где f и g — многочлены над некоторым полем (при этом g ne 0, а f и g не имеют общих делителей, кроме констант).

Определение. Элементы a и b кольца, для которых 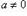, , но ab = 0, называются делителями нуля. Кольцо без делителей нуля называется также областью целостности.

Теорема 1. Из ab = ac следует b = c, если только и не является делителем нуля.

Доказательство. Из ab = ac следует ab — ac = 0 или a(b — c) = 0. Но так как 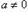и не делитель нуля, то b — c = 0, b = c.

В дальнейшем нам придется иметь дело исключительно с кольцами без делителей нуля. Для них из ab = ac и следует b = c.

При умножении справедливы обычные правила знаков, а именно:

Теорема 2. Поле не имеет делителя нуля, т. е. если ab = 0, то либо a = 0, либо b = 0.

Доказательство. Если ab = 0 и a ≠ 0, то, умножая обе части равенства на a -1 , найдем 1 · b = a -1 · 0, т. е. b = 0.

Итак, поле является кольцом без делителей нуля. Утверждение, обратное этому, вообще неверно: существуют кольца без делителей нуля (например, кольцо целых чисел), не являющиеся полями. Однако для конечных колец обратная теорема также верна. А именно:

Теорема 3. Всякое конечное кольцо без делителей нуля, содержащее более одного элемента, является полем.

Доказательство. Достаточно проверить свойство VII. Пусть a ≠ 0. Каждому элементу x кольца поставим в соответствие элемент y =ax. Если x₁ ≠ x₂, то также y₁ ≠ x_y, т. к. иначе ax₁ = ax₂ и x₁ = x₂(Теорема1).Значит, x → y есть взаимно однозначное отображение всего кольца R на некоторое его подмножество M, т. е. R

M. Но по основнай теореме о конечных множествах (Конечное множество не равномощно никакому его собственному подмножеству и собственному надмножеству) конечное множество R не равномощно своему собственному подмножеству. Поэтому R = M, т. е. для любого элемента 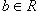существует в R элемент q такой, что q → b, т. е. aq = b, что и доказывает VII.

Так как все элементы поля, отличные от нуля, образуют по умножению коммутативную группу, то для любого элемента a ≠ 0 степень a n определена при любом целом показателе n.

Для частного элементов любого поля верны те же правила оперирования, что и для обыкновенных дробей.

Простые поля

Подполе. Простое поле. Множество M поля P называется подполем P, если оно само является полем при тех же операциях сложения и умножения, которые заданы в поле P. Тогда P называется надполем или расширением поля M.

Так, поле рациональных чисел является подполем поля действительных чисел, а последнее — подполем поля комплексных чисел.

Теорема 1. Для того чтобы множество M поля P, содержащее не менее двух элементов, было подполем, необходимо и достаточно, чтобы сумма, разность, произведение и частное (если только оно существует в P) любых элементов из M снова принадлежали к M.

Доказательство вполне аналогично проведенному для соответствующей теоремы о кольцах (теорема о кольцах: Для того чтобы непустое подмножество M кольца R было его подкольцом, необходимо и достаточно, чтобы сумма, разность и произведение любых двух элементов из M снова принадлежали M.).

Всякое подполе M поля P содержит 0 как разность a — a, где , и единицу как частное , где , a ≠ 0.

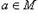
Теорема 2. Пересечение (в смысле пересечения множеств) любого множества надполей поля P опять является подполем поля P.

Соответствующая теорема верна и для колец, т. е. пересечение любого множества подколец кольца R есть подкольцо кольца R. Доказательство ее вполне аналогично данному здесь для полей.

Доказательство. Пусть <M_s> есть некоторое множество подполей, где индексы s образуют множество S и — пересечение всех подполей M_s данного множества; 0 и 1 входят в каждое подполе M_s и, значит, в D. Итак, D содержит не менее двух элементов. Если aиb — элементы D, то они входят в каждое M_s и по теореме 5 a + b, a — b, ab, а при b ≠ 0 и также входят в M_s, а значит, и в D. В силу теоремы 5 D — подполе поля P.

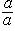
Поле, не имеющее подполей, отличных от него самого, называется простым.

Примерами простых полей могут служить поле рациональных чисел и поля вычетов по простому модулю p.

Любое подполе M поля P рациональных чисел содержит число 1, а значит, и все его кратные n · 1 = n, т. е. все целые числа, а значит, и все их частные, т. е. все рациональные числа. Итак, M = P, т. е. P — простое поле. Точно так же любое подполе M поля C_pвычетов по простому модулю p содержит класс (1), служащий единицей C_p, а значит, любой класс (r) как r-кратное класса (1). Итак, M= C_p, т. е. C_p — простое поле.

Можно доказать, что этими полями в некотором смысле исчерпываются все простые поля.

Теорема 3. Любое поле содержит простое подполе и притом только одно.

Доказательство. Поле P вообще содержит подполя (например, само P). Пусть D есть пересечение всех подполей поля P. По теореме 6 D является подполем P и по самому определению входит в любое подполе. Пусть M — подполе D, отличное от D.

Из определения подполя следует, очевидно, что M будет подполем и для P, и D не входит в M, что невозможно. Итак, D — простое подполе P. Если D’ — также простое подполе поля P, то пересечение будет опять подполем поля P, причем и . Но из определения подполя следует, что в таком случае D» будет подполем как для D, так и для D’, а так как D и D’ — простые подполя, то D = D» = D’, чем доказана единственность простого подполя.

Расширения полей

Расшире́ние по́ля K — поле E, содержащее данное поле K в качестве подполя. Исследование расширений является важной задачей теории полей, так как любой гомоморфизм полей является расширением.

Базовые определения

Если E — поле, его подполе — это его подмножество K, замкнутое относительно сложения и умножения, взятия обратного и противоположного элементов и содержащее единицу, на котором введены те же операции, что и в поле E. В этом случае E называется расширением поля K, заданное расширение обычно обозначают Esupset K (также используются обозначения E/K и Ksubset E). Любой гомоморфизм полей инъективен, то есть является вложением. Из этого следует, что задание конкретного расширения Esupset K эквивалентно заданию гомоморфизма f:Kto E.

Если задано расширение Esupset K и подмножество S поля E, то наименьшее подполе E, содержащее K и S, обозначается K(S) и называется полем, порождённым множеством S над полем K. Расширения, порождённые одним элементом, называются простыми расширениями, а расширения, порождённые конечным множеством — конечно порождёнными расширениями.

Для любого расширения Esupset K E является векторным пространством над полем K. В этой ситуации элементы E можно понимать как «векторы», а элементы K — как «скаляры», умножение вектора на скаляр задаётся операцией умножения в поле E. Размерность этого векторного пространства называется степенью расширения и обозначается [E:K]. Расширение степени 1 называется тривиальным, расширения степени 2 и 3 — квадратичными и кубическими соответственно. Расширение конечной степени называют конечным, в противном случае — бесконечным.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 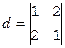, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

В дальнейшем станем действовать аналогично, к тому же не будем педантично ставить индекс +_n, ×_n около символов операций, обозначая их просто + и
× , если значение индекса n ясно из контекста.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре опре­делителя:

.

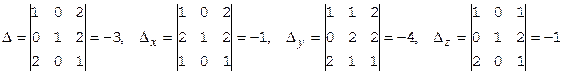
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

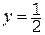
Сделаем проверку (символом Þ обозна­чен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найден­ные значения вычетов удовлетворяют сис­теме уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

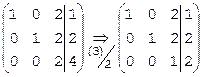
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .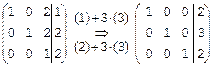

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Видео:Матричный метод решения систем уравненийСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )

Ввод: -1,15
Результат: ( -115 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Немного теории.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.

📸 Видео

Решение системы уравнений методом Крамера.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Решение системы уравнений методом ГауссаСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем уравнений методом подстановкиСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение систем уравнений методом сложенияСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Решение системы линейных уравнений методом ГауссаСкачать

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать