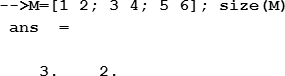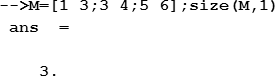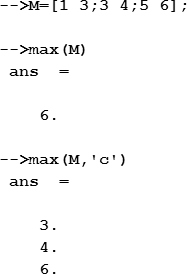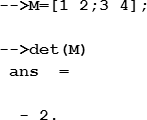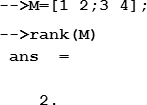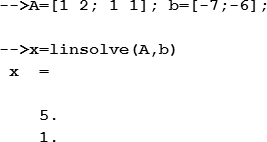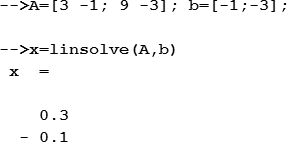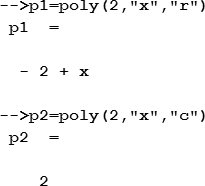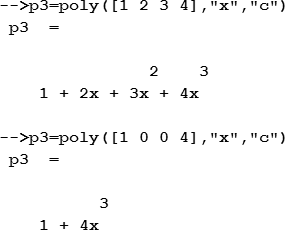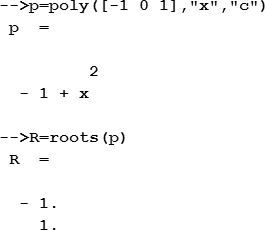Решить систему линейных алгебраических уравнений в scilab

Видео:Решение систем линейных уравнений в Scilab.aviСкачать

Сопромат .in.ua

изучаем сопротивление материалов

Видео:Решение трансцендентных уравнений в Scilab.aviСкачать

Некоторые варианты решения системы уравнений

Видео:Решение уравнений в ScilabСкачать

Решение online

На странице “Решение системы линейных уравнений“ вы можете решить систему до 10 уравнений online.

Видео:Решение системы уравнений методом Крамера.Скачать

Решение системы линейных алгебраических уравнений в OpenOffice.org

Из линейной алгебры нам известно, что для системы линейных уравнений A*x=b решением 1 есть x=A -1 *b, если детерминант матрицы A не равен нулю. Здесь A -1 – обратная матрица коэффициентов СЛАУ .

Решим систему из двух уравнений.

В ячейках (A1:B2) вводим данные.
Детерминант матрицы: MDETERM(A1:B2)

Затем получаем обратную мартицу A -1 :
=

Умножаем полученную обратную матрицу на столбик з правою частью систем уравнений:
=

Осталось проверить проверить правильность решения, подставив полученные неизвестные в систему уравнений.

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Пример решения системы линейных уравнений в Scilab

Scilab — мощный открытый пакет прикладных математических программ (система компьютерной математики) для инженерных и научных расчётов.

• решать задачи линейной алгебры;
• решать нелинейные уравнения и системы;
• решать задачи оптимизации;
• дифференцировать и интегрировать;
• решать обыкновенные дифференциальные уравнения и системы.
• обрабатывать экспериментальные данные (интерполяция и аппроксимация, метод наименьших квадратов);
• создавать различные виды графиков и поверхностей.

Более подробно с пакетом можно ознакомится на домашней странице Scilab или в википедии

Пример

Решим систему из двух уравнений вида A*x=b

Задаем матрицу коэффициентов: —>A=[1,2;3,4] A = 1. 2. 3. 4. Задаем вектор свободных коэффициентов: —>b=[2;1] b = 2. 1.

Определяем детерминант матрицы: —>det(A) ans = — 2 Так как определитель матрицы отличен от нуля, решение СЛАУ существует.

Решение СЛАУ методом обратной матрицы —>x=Ab x = — 3. 2.5 Запись Ab соответствует математической операции A -1 b. Записи x=Ab эквивалентна запись x=inv(A)*b

Эту систему уравнений также можно решить с помощью специальной функции linsolve (эта функция решает уравнение вида Ax+b=0, поэтому поменяем знак вектора b) x=linsolve(A,-b) x = — 3. 2.5 и получили ответ: x₀= -3; x₁= 2.5;

Проверяем A*x-b ans = 1.0D-14 * 0.2220446 0.3552714 результирующий вектор близок к нулю, то есть система решена верно.
Существуют и другие способы решения системы линейных уравнений в среде Scilab.

Видео:Решение системы уравнений методом ГауссаСкачать

Пример решения системы линейных уравнений в среде программирования R

R — язык программирования для статистической обработки данных и работы с графикой, а также свободная программная среда вычислений с открытым исходным кодом.

Пример

Решаем систему Ax=b (из двух уравнений)

A A [,1] [,2] [1,] 1 2 [2,] 3 4 > b b [1] 2 1 > x x [1] -3.0 2.5 и получили ответ: x₁= -3; x₂= 2.5;

Проверка: > A %*% x [,1] [1,] 2 [2,] 1

Определитель матрицы: > det(A) [1] -2

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы линейных уравнений Ax=b в Euler Math Toolbox

Домашняя страница Euler Math Toolbox . В пакет интегрирована система компьютерной алгебры Maxima. Система напоминает Matlab, но имеет собственный стиль, и немного иной синтаксис.
Домашняя страница автора René Grothmann

Пример

This is Euler Math Toolbox, Version 5.8. >A:=[1,2;3,4] 1 2 3 4 >b:=[2;1] 2 1 >x:=Ab -3 2.5 Получили ответ: x₀= -3; x₁= 2.5;

Определитель матрицы: >det(A) -2

Проверка: умножим A на x (операция умножения обозначается точкой «.») >A.x 2 1

Решить указанную систему можно также с помощью следующего выражения (inv(A) — обратная матрица) >x:=inv(A).b -3 2.5

1 Этот способ решения называется — решение СЛАУ методом обратной матрицы

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Основы работы с системой технических расчетов Scilab

Решение задач линейной алгебры

Функции для нахождения числовых характеристик матриц

Для определения количества строк и столбцов матрицы М используют функцию size, аргументом которой является имя массива:

Если нужно определить количество только строк или только столбцов, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «1» или «r», если следует определить количество строк, «2» или «с» — если столбцов. Например:

Общее количество элементов матрицы или длину вектора вычисляет функция length, аргументом которой является имя матрицы или вектора:

Для определения максимального значения элемента матрицы или вектора используется функция max, аргументом которой является имя матрицы или вектора. Если нужно определить максимальное значение для каждого из строк или столбцов матрицы, то синтаксис функции модифицируется: добавляется второй аргумент, который имеет значение «r», если следует определить максимальное значение для каждой строки, или «c» — если для каждого столбца:

Аналогично используется функция min, предназначенная для определения минимального значения элемента матрицы или вектора.

Для вычисления определителя (детерминанта) квадратной матрицы используется функция det, аргументом которой является имя матрицы:

Для вычисления ранга матрицы используется функция rank, аргументом которой является имя матрицы:

Функции, реализующие численные алгоритмы решения задач линейной алгебры

Вычисление матрицы, обратной М

Напомним, что обратной по отношению к матрице М называется такая матрица, которая при ее умножении на матрицу М дает единичную матрицу.

Как видим, обратная матрица А достаточно близка к единичной, но все же полностью ею не является, что является следствием погрешности численных вычислений.

Scilab позволяет решать системы линейных алгебраических уравнений вида Ax=b. В документе для значений A формируется матрица коэффициентов при неизвестных, каждая строка которой содержит коэффициенты одного уравнения, а для значений b формируется вектор-столбец из свободных коэффициентов.

После этого для решения системы используется функция linsolve, имеющая такой синтаксис:

где A — это матрица коэффициентов при неизвестных, b — вектор-столбец свободных коэффициентов.

Функция возвращает найденные значения неизвестных системы в виде вектора.

Таким образом, решение системы линейных уравнений 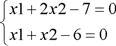имеет вид:

Искомые значения: х1=5, х2=1.

Если система не имеет решения, то об этом выдается сообщение «WARNING: Conflicting linear constraints!» (Конфликтующие условия для линейных уравнений). Например, такая ситуация возникнет при попытке решения системы линейных уравнений :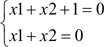

Система линейных алгебраических уравнений может иметь множество решений. В таком случае функция возвращает только одно. Ниже приведен пример такой ситуации при решении системы линейных уравнений :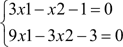

Работа с полиномами

Напомним, что полиномом или алгебраическим уравнением называется уравнение вида a₀x n + a₁x n-1 + . + a_n-1x + an.

Для создания полинома используется функция poly.

где р — это имя полинома (его можно и не задавать).

Аргументы функции: a — матрица или вещественное число, x — символьная переменная, «flag» — символьная переменная, которая определяет способ задания полинома и имеет значение «roots» (допускается сокращение «r») или «coeff» («c»). По умолчанию — «roots». Если «roots» имеет значение «r», то полином создается с параметрами a_i для соответствующих символьных переменных x_i. Если «flag» имеет значение «c», то значения параметров a_i воспринимаются как корни, для которых нужно рассчитать коэффициенты полинома.

Следующий пример демонстрирует использование функции poly для создания полиномов р1, который имеет корень «2» и р2 с коэффициентом «2»:

В следующих примерах создаются полиномы с соответствующими коэффициентами для кубического уравнения.

С полиномами можно производить действия умножения, создавать из них дроби (деление), складывать и вычитать.

Решение уравнения с одним неизвестным

Scilab может решать алгебраическое уравнение с одним неизвестным. Например, нужно найти корни уравнения x 2 = 1. Если — как в данном примере — уравнение не имеет вида полинома, то его следует предварительно преобразовать в полином: x 2 — 1 = 0. После этого используется функция roots, единственным аргументом которой является имя полинома. Функция возвращает найденные корни полинома.

Если уравнение не имеет решения на множестве вещественных чисел (x 2 + 1 = 0), то Scilab ищет решение среди комплексных чисел:

Вычисление сумм элементов матрицы

Для вычисления суммы значений элементов матрицы используется функция sum.

Если следует вычислить отдельно сумму значений для каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».

Вычисление произведения элементов матрицы

Для вычисления произведения используется функция prod.

Если следует вычислить отдельно произведение значений каждого столбца, то вторым аргументом функции является число «1» или буква «с», а если для строки, то — «2» или буква «r».

Дифференциалы

Для нахождения дифференциалов в определенной точке используется функция numdiff, первый аргумент которой является именем функции, которую нужно продифференцировать, а второй — координата точки, в которой нужно вычислить производную.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Метод Крамера в Scilab
презентация к уроку по информатике и икт на тему

Решение систем линейных уравнений с несколькими неизвестными методом Крамера в программе Scilab. Интегрированное занятие для дисциплин информатика и математика в СПО.

Видео:Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

Скачать:

Предварительный просмотр:

Видео:6 способов в одном видеоСкачать

Подписи к слайдам:

Авторы проекта: Зыбина А.С. Пашикина С.И . Решение систем линейных уравнений с несколькими неизвестными методом Крамера в программе Scilab . Интегрированное занятие для дисциплин информатика и математика в СПО.

Основные понятия Рассмотрим систему трёх линейных уравнений с тремя неизвестными: где — неизвестные, — коэффициенты ( ), — свободные члены. Тройка чисел называется решением системы трёх линейных уравнений с тремя неизвестными , если при подстановке их в уравнения системы вместо получают верные числовые равенства. Если система трёх линейных уравнений имеет хотя бы одно решение, то она называется совместной . Если система трёх линейных уравнений решений не имеет, то она называется несовместной . Если система трёх линейных уравнений имеет единственное решение, то ее называют определенной ; если решений больше одного, то – неопределенной . Если свободные члены всех уравнений системы равны нулю , то система называется однородной , в противном случае – неоднородной .

Метод Крамера Пусть нам требуется решить систему трёх линейных уравнений с тремя неизвестными: (1) в которой определитель системы (он составлен из коэффициентов при неизвестных) ∆≠0, а определители получаются из определителя системы ∆ посредством замены свободными членами элементов соответственно первого, второго и третьего столбцов. Теорема (правило Крамера ). Если определитель системы ∆≠0 , то рассматриваемая система (1) имеет одно и только одно решение, причём

Решите систему методом Крамера : Решение: Вычислим определитель системы: Так как определитель системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера . Составим и вычислим необходимые определители :

Решим систему методом Крамера : Находим неизвестные по формулам Крамера : Ответ:

Решение систем линейных уравнений в программе SCILAB Для решения подобных систем уравнений в Scilab существует функция linsolve . Обращение к ней выглядит следующим образом: linesolve ( K,k ) . K — таблица, составленная из коэффициентов уравнений системы, причем она сформирована таким образом, что каждая строка представляет собой список коэффициентов одного из уравнений системы, а каждый столбец — список коэффициентов при одноименных переменных, то есть если первым элементом в первой строке является коэффициент при y , то первыми элементами других строк также должны быть коэффициенты при y в соответствующих уравнениях. Общий вид K : K =

Для решаемой системы: К= k — столбец, содержащий свободные (стоящие после знака «=») коэффициенты. Примечание: при задании в Scilab k должен быть именно столбцом , поэтому перечисление переменных нужно делать через «;» Общий вид: Для решаемой системы k = к = :

После того как элементы списков K и k определены, приступим к решению системы в Scilab

Второй корень ( 5.888D-16 ) нужно округлить. Получится 0. Таким образом, решение системы принимает вид: (4; 0; -1). Для проверки можно посчитать детерминанты (определители) матриц отдельно. Процесс будет более длительным. Рассмотрим такой способ решения.

Задание для самостоятельной работы : решить систему уравнений с помощью системы Scilab и проверить полученное решение вручную.

Видео:Решение системы линейных уравнений в MapleСкачать

По теме: методические разработки, презентации и конспекты

Двумерные массивы (прямоугольные таблицы). Информационная модель решения системы линейных уравнений с двумя неизвестными методом Крамера.

На уроке мы изучаем метод Крамера для решения системы линейных уравнений, основанный на вычислении определителя прямоугольной матрицы, и составляем информационную модель вычисления корней с испо.

Презентация «Метод Крамера для решения систем уравнений»

Цель: познакомить студентов с методом Крамера для решения систем линейных уравненийМетодические рекомендации: презентация предназначена для демонстрации метода Крамера. Не содержит теоретическог.

Тема: «Определитель второго порядка. Решение системы двух линейных уравнений с двумя переменными методом Крамера» (2 ч)

План открытого урока по математике.

решение систем методом Крамера и Гаусса

Методическая разработка по проведению обобщенного и систематизированного урока с применением различных методов обучения на каждом этапе урока окажет помощь в совершенствовании процесса обучения, а так.

Разработка бинарного урока на тему: «Решение систем алгебраических уравнений методом Крамера»

Достижения профессиональной компетентности обучающегося ГАОУ СПО «Нижнекамский политехнический колледж им.Е.Н.Королева» обеспечивается интеграцией двух групп компетенций: профессиональных и общи.

Методическая разработка для проведения занятия по теме «Решение систем линейных уравнений методом Крамера»

Тема урока: Способы решения линейных систем уравненийТип урока: урок первичного ознакомления с материаломДлительность: 1 час 20 мин.Технология — развитие критического мышления через чтение и письмоЦел.

Самостоятельная работа по теме «Решение систем линейных уравнений методом Крамера»

Самостоятельная работа по теме «Решение систем линейных уравнений методом Крамера». В самостоятельной работе представлено 5 вариантов с решением.

🎥 Видео

Решение системы линейных уравнений. MaximaСкачать

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Матричный метод решения систем уравненийСкачать

Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать