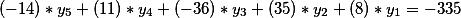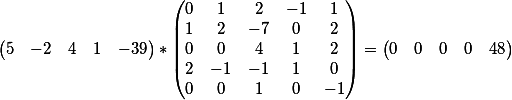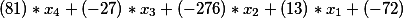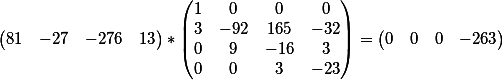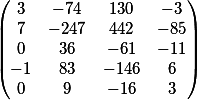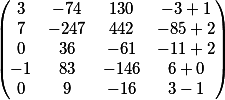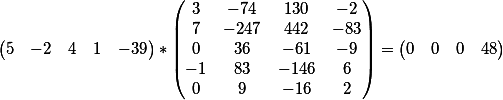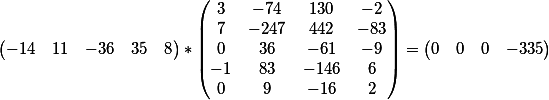Как и обещал в первой своей статье, я хочу ознакомить Вас с одним из методов решения системы диофантовых уравнений. Цель статьи ознакомить остальных читателей с этой методикой и донести её в более или менее понятном виде.
Рассмотрим систему из двух диофантовых уравнений
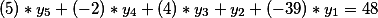
и
Найдем все возможные решения первого уравнения. Как, спросите Вы? Наверняка есть разные методики, но я поделюсь в одной из следующих статей, как бы я решал подобную задачу. А сейчас просто примем что общее решение имеет вид
Как проверить что я не лгу?
получили в результате значение свободного члена, а следовательно вычисления правильные
Следующим этапом мы подставим наше общее решение
во второе уравнение
Процедура такая же: умножаем вектор из коэффициентов второго уравнения на общее решение первого
получаем вот такой результат
то есть мы получили уравнение вида
С правой стороны второго диофантового уравнения как был свободный член равный -335, так и остался, то есть наше окончательное решение на этом этапе имеет вид
Или перенеся свободные члены в правую сторону получим
Итак, мы получили очередное диофантовое уравнение. Давайте найдем его общее решение и проверим его на истинность.
то есть общее решение имеет вид
А теперь делаем обратное преобразование(пусть так называется). То есть в систему
Мы вместо неизвестных x подставляем то, что получилось на последнем этапе
В матричном исчислении это решается умножением одной матрицы на другую.
Но с первой матрицей надо сделать определенную процедуру: убрать (временно) последний столбец с свободными членами, так как этот параметр не участвует в умножении, и будет пользоваться позднее.
Последний столбец это свободные члены этой системы.
Учтем тот столбец который временно удаляли, перед умножением и сложим их
наш окончательный ответ в виде матрицы
Векторное произведение коэффициентов первого уравнения и матрицы
а векторное произведение коэффициентов второго уравнения и матрицы
Как видим, результат совпадает с свободным членом каждого из уравнений.
Таким образом общее решение имеет вид
где m,p,q — могут принимать любые целые значения
Таким незамысловатым способом можно решать и более сложные линейные диофантовые уравнения. По следам этого алгоритма создан калькулятор правда, этот калькулятор очень не любит когда вместо значений в коэффициентах первого уравнения начальной системы встречаются нули. Но это проблема конкретной моей реализации этого алгоритма.
В следующей теме я расскажу как создавать диофантовые уравнения по матрице общего решения. Задача в общем то банальна и делается в одно действие, но вдруг кто то не знает.
Буду благодарен за замечания, отзывы и предложения.
- Решение системы из двух однородных диофантовых уравнений
- Решение систем линейных диофантовых уравнений Текст научной статьи по специальности « Математика»
- Похожие темы научных работ по математике , автор научной работы — Малашонок Г. И.
- Текст научной работы на тему «Решение систем линейных диофантовых уравнений»
- 💥 Видео
Видео:Матричный метод решения систем уравненийСкачать

Решение системы из двух однородных диофантовых уравнений
| Коэффициенты первого диофантового уравнения | |
| Коэффициенты второго диофантового уравнения | |
| Система двух диофантовых уравнений |
| Матрица общего решения |
| Результат в виде строки |
| Проверка для первого уравнения |
| Проверка для второго уравнения |
Рассматривается оригинальный алгоритм решения двух произвольных однородных линейных уравнений в целых числах. Автоматический расчет матрицы решений.
Пусть Нам надо решить систему из двух диофантовых уравнений
Несомненно можно решать эту систему так как делают все.
— Умножив первое уравнение на 31 и вычтя из второго мы получим классическое диофантовое уравнение с двумя переменными.
— Решив которое можно найти все целочисленные значения системы
Схема рабочая, несмотря на множество ручных вычислений
Мне такой подход не нравится и для решения мы будем использовать другой метод.
Он красив и понятен даже для школьников, знающих про вектора и матрицы.
Частично использован алгоритм, описанный вот в этой статье ( стр 36,37)
Он доработан, приведен к матричным операциям и обобщен на любые значения.
Алгоритм и его работу мы будем изучать на примере.
Решаем следующую систему диофантовых уравнений
Мы этот пример взяли по причине, что в интернете его решали и для него вывели общее решение. Так что есть с чем сравнивать.
1. Находим общее решения первого уравнения из заданной системы. Например пусть будет такое. Но мы можем воспользоваться и онлайн калькулятором общее решение линейного диофантового неоднородного уравнения ответ которого будет равноценен.
Как видим ответ совпадает со свободным членом первого уравнения.
2. Теперь, раз мы нашли общее решение первого уравнения, давайте его подставим во второе.
То есть в уравнение (70a-31b+9c=9)подставим наши значения
Можно руками подставлять и сокращать подобное, но в матричном исчислении мы лишь умножаем вектор на нашу матрицу.
То есть мы получили уравнение
Но, обратите внимание, что во втором уравнении свободный член равен не нулю, а девяти.
То есть мы переписываем
Переносим свободные члены в правую часть и получаем классическое диофантовое уравнение, которое можем решать легко.
Общее решение такое
3. А теперь делаем обратное преобразование.
вот в эту систему (begina=8m+14p+20\b=-19m-30p-44\c=-m+p+0end)
мы вместо неизвестных подставляем найденные m и p.
В матричном исчислении это решается так:
последний столбец. Это свободные члены и они нам пока мешаются.
Умножаем эту матрицу на матрицу созданную из этих уравнений
Последняя колонка это свободные члены, прибавим к ней ту колонку которую убирали в начале этого пункта
то есть к вектору <-22 36 -11> прибавляем
А следовательно общее решение системы двух диофантовых уравнений
Проверим, правильно ли посчитали
Для первого уравнения
Как видим значения свободных членов совпадают с значениями в правой части уравнений, а следовательно мы получили общее решение.
Но радоваться рано, несмотря на то, что мы получили общее решение, мы получаем не все возможные значения.
Почему? Да потому что вектор имеет НОД =19
и фактически наше общее решение имеет вид
Так как числа в скобках должны быть целыми, то обозначим их t и наше, уже точно окончательное общее решение системы двух диофантовых уравнений имеет вид
Еще несколько примеров, и небольшие ремарки к алгоритму.
Теперь что калькулятор не может.
Очень сильно не любит уравнения с нулевыми коэффициентами. Особенно первое. Например, вот такую систему
калькулятор не решит.
Прибавим к первому уравнению, второе. Таким образом в первом уравнении исчезают все нулевые коэффициенты и калькулятор сможет решить эту систему. Ну как не решит? Решит, если прибегнем к уловке, и постараемся убрать все нулевые коэффициенты
Проверка показывает что общее решение корректно.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Решение систем линейных диофантовых уравнений Текст научной статьи по специальности « Математика»
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Похожие темы научных работ по математике , автор научной работы — Малашонок Г. И.
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Текст научной работы на тему «Решение систем линейных диофантовых уравнений»
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ ДИОФАНТОВЫХ УРАВНЕНИЙ
Malashonok G.I. Solving systems of linear Diophantine equations. New methods to solve linear systems of Diophantine equations are proposed. These problems are considered from two points of view — modular and p-adic. Both methods allow obtaining solutions of a linear system with the size nxjn with the complexity 0(np + lm). For quasi-square systems, the p-adic method allows obtaining solutions with the complexity 0(n3). Both estimations have the accuracy up to the logarithmic multipliers, /3 being the power in the estimation of matrix multiplication time.
Задачи, в которых ищутся целочисленные решения алгебраических уравнений, относятся к одним из самых старых задач в математике, которые неизменно привлекали к себе внимание.
Основной метод для решения линейных систем диофантовых уравнений основан на вычислении формы Смита матрицы коэффициентов системы [1, 2]. В недавних работах были получены вероятностные методы для нахождения решений линейной системы диофантовых уравнений [3, 4]. Вероятностные методы являются самыми быстрыми из известных сегодня методов. Однако они не гарантируют нахождение решения. Если решение не найдено вероятностным методом, то всегда существует вероятность того, что система совместна, но ее решение не найдено случайно.
В настоящей статье предлагаются детерминистские р-адический и модулярный методы, которые не связаны с вычислением формы Смита матрицы коэффициентов. Оба метода сводят задачу к решению системы в кольце вычетов.
Первый из них, с пощью р-адического подьема, вычисляет базисное множество точек на гиперплоскости всех решений системы. А затем вычисляет все целые точки на этой плоскости.
Второй метод основан на преобразовании к эквивалентной системе с левым квадратным блоком, имеющим диагональный вид. Его диагональные элементы равны определителю соответствующего блока исходной матрицы. Вычисления выполняются с помощью китайской теоремы об остатках. А затем решается систе-
ма по модулю этого определителя. Кроме того удается объединить детерминистские и вероятностные методы. Когда решение не получено вероятностным методом, то процесс решения продолжается до установления несовместности системы или построения всех решений системы детерминистским р-адическим методом.
Показано, что для квазиквадратных систем сложность р-адического метода 0(п3), а модулярного 0(п^+1). Для существенно прямоугольных систем, когда число неизвестных т более чем вдвое превышает число уравнений п, оба метода имеют одинаковый порядок сложности — 0<п^+1т). Здесь оценки приводятся с точностью до логарифмического множителя и предполагается применение стандартного умножения. /3 — показатель степени в оценке сложности матричного умножения.
Приводится алгоритм со сложностью 0(пР
1т) для решения систем над кольцами вычетов.
Как обычно, все результаты переносятся с кольца целых чисел на кольцо полиномов над полем.
Пусть И, — коммутативное кольцо с единицей. Будем называть диофантовой матрицей для ненулевой пары а из И.2 унимодулярную матрицу Еа € Я2*2 такую, что
Еаа = ^ ^ V 9 ± 0, И., выбирающую представителя класса смежности для р’ е К. в прообразе -1(р/):
а’ = (?)€в /2 диофантову матрицу Еа>
следующим образом Еа> = ф(Еа). Очевидно, такое определение корректно, так как
Еа’С1 = ^ о = 1, §’ Ф 0-
Покажем, что д’ = ф(д) ф 0.
Из-за обратимости диофантовых матриц р и д делятся на д. Поэтому если ф(д) = 0,
диофантова матрица для а и Епа =| » ). Определим для ненулевой пары
то ф(р) = ф(д) = 0, но по условию хоть одно из чисел р’ = ф<р)^д' = ф<я) не должно быть нулем.
Следовательно, множество квазиевклидовых колец содержит все 67 кольца и их факторко-льца, в том числе евклидовы кольца и их фак-торкольца.
Будем называть матрицу А = (а^-), размера пхт, верхней треугольной, если все элементы под главной диагональю нулевые: (г, ]) = 0 для всех п > ] > г > 1. Заметим, что элементы на главной диагонали и над ней могут тоже быть нулевыми.
Будем говорить, что матрица А разложима, если она является произведением унимодулярной матрицы А на верхнюю треугольную матрицу Л: А — А А.
Предложение 2. В квазиевклидовом кольце все матрицы разложимы.
Построим такое разложение для матрицы А = (ау), размера п х т. Пусть
** = ( £ )’ * > * *- ■ ‘ матрица для а^. Обозначим через Е™х> унимо-дулярную матрицу, которая получается после замены в единичной матрице порядка п четырх элементов 3. Пусть Е$ = Еап^ • ■ • Еаз+1>я и = Еп- • • • Е. Тогда и — унимодулярная матрица, и А — верхняя треугольная матрица. Эти вычисления приводят к последовательному исключению ненулевых элементов сначала в первом столбце, затем во втором столбце, и так далее до п — 1-го столбца.
асимптотическую оценку сложности вычисления диофантовой матрицы, М(п) — асимптотическую оценку сложности умножения матриц порядка п, М<п) — ап^. Известное сегодня значение для /3 меньше 2,356
Лемма 1. Пусть И. — квазиевклидово кольцо, А,С 6 КпХп, А — верхняя треугольная матрица. Тогда матрицу ^ ^ ^
асимптотической оценкой сложности, не превосходящей
Доказательство. Для разложения матрицы размера 2 х 1 достаточно умножить на ее диофантовую матриц>’. Пусть теперь п = 2Р, р > 0.
Разобьем А и С на квадратные блоки
Пусть имеются четыре разложения:
Матрицы Qi = ( ), г = 1,4, уни-
модулярные, а, аь «2, с?, ^1, с?2 — верхние треугольные. Тогда получим Л =
Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
7з 2т и С2(п,тп) = (7г — т)тСр+ +с*(п — тп)^-2(Адттг(тг — т) + Ютпп — 4/г.2 — 477г2), при тп 2т и т делит тг. Сначала выполним разложение для матрицы, образованной блоком А и верхним квадратным
блоком С матрицы С: Ц)-*( 0>
Затем (тг —2тп)/тп раз проведем разложение матрицы, образованной блоком А на предыдущем шаге и г-тым сверху квадратным блоком Сі матрицы С, г = 2. к. Перемножение уни-моду лярных матриц, получаемых на каждом шаге, требует еще четырех умножений матриц размера т х т. Всего получим
л1. . л/ .(п — т) . (тг — 2т)
ф — унимодулярная, А2 — верхняя треугольная. Обозначим ^ ^2 ^ = С> ^ р1 ^.
(3). Пусть имеется разложение блока Их :
Обозначим й2 = 0.
Тогда разложима матрица А:
Л = Ша8(1, 6,) Я ШаВ(А, 1), А = ( А02 ) .
Всего, при таком разложении, требуется 9 блочных умножений, два блочных разложения
и одно разложение для блока размера п х п/2. Обозначим Ct(n) сложность разложения матрицы А. Получим
По лемме 1 получим
Будем разбивать блоки А и D далее на квадратные блоки. И так будем поступать вплоть до блоков второго порядка. При этом асимптотическая оценка сложности вычислений будет
Ct(n) = EL, 2‘-‘Ш2Со + а(9 + А„)(п/2‘)») og6 = 23/4.
Следствие 2. В квазиевклидовом кольце разложение прямоугольной матрицы А размера п х т можно выполнить с асимптотической оценкой сложности, не превосходящей Ct°(n, т) = Ср(п2 — п)/2 + от/3(цр + (га — п)/п) при п 2т.
Доказательство сразу следует из оценок для Ct(n) и С8(п).
При 71 т достаточно разложить верхний квадратный блок и воспользоваться следствием Леммы 1.
Теорема 2. В квазиевклидовом кольце всякая система линейчых уравнечий Ау = с с верхней треугольчой матрицей коэффици-ечтов A G
может быть решеча с асимптотической оцечкой сложчости
Сп = CD(n2 — п)/2 + афрпр,
Решение системы Ау = с можно свести к решению двух систем вдвое меньшего размера и одному матричному разложению.
блочная запись системы Ау = с. Все блоки матрицы А квадратные, блоки А, И — верхние треугольные.
(1). Пусть решением системы Иуо = її будет Уо = Узо + V, У Є Кл/2хп/2^ у 8о £ БГ1/2, «о — вектор параметров. Подставим его в систему Аух + Вуо = /. Получим Ауі+б^о = где С = ВУ, д = / — £г>.
(2). Разложим матрицу (А, Є):
(А,Є)Р = (Л,0). Р — унимодулярная
матрица, А — верхняя треугольная. По лемме 1 и замечанию к лемме оценка сложности такого разложения матрицы (А, С) составляет Са(п/2).
(3). Пусть решением системы Аг = д будет гх = Wtl+w,W е К*/2хп/25 гУ)іі € Кп/2> ^ _
Т°ГЛа ( го ) =*•«(*.!)( £ ) + ( будет решением системы (Л, 0) ( 21 ) = д.
блочная запись матрицы Р. Так как ^ ^ ^ и
Уо = + г», то решение исходной системы
Лу = с получим в виде
Всего требуется выполнить пять блочных умножений. Обозначим Сп сложность решения системы порядка п. Тогда Сп = 2Сп/2 + 5М(п/2) + С&(п/2) =
= 2Сп/2 + ск(5 + р)пП: 2 + (п/2)2Ср.
Отсюда получаем асимптотическую оценку
Сп = Со(п2 — п)/2 + афрп13,
1 п, А’ = (А, В), А -квадратный блок, имеющий верхний треугольный вид. По замечанию к лемме 1 можно построить унимодулярную матрицу т) + С1(т>п) +Сп + м (п)(т/п),
г = 1,2, где г = 1 соответствует случаю т > 2п, г = 2 соответствует случаю 2п>т> п.
квадратный блок, имеющий верхний треугольный вид. По теореме 2 решение системы Ах = с! можно получить за Ст операций, согласно теореме 2. Следовательно, общее число операций для этого решения будет
Спт — Сь(п, т) Ст і 1» 2,
где i = 1 соответствует случаю 2т > п > т, г = 2 соответствует случаю гг > 2т.
Утверждение теоремы получается подстановкой всех оценок в правую часть.
В частности, для случая квадратной матрицы коэффициентов системы получим
С’пп = п2Со + осфрцР, Фр = —
Для (3 = 3: фр Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Если рассматривать (£,у,и>) как вектор неизвестных, то получим систему уравнений
Домножая каждую часть на обратимую в К матрицу
приходим к системе
Пусть система (5) имеет диофантово решение
2 = (у^) € Я711. Тогда совместна система (7). Следовательно, совместна и система
(6). Наоборот, пусть совместна система (6) и
— ее решение, тогда ( п по формуле (3) получим асимптотические оценки числа операций соответственно для Z и F[x] :
Г)ркпМ (n)(og\A\ +0.5 log п)2
При А; п получим соответственно для Z и F[a-]:
0(п/3+1т(log ||А|| 4- log77.)2),
0(7z^+17Tideg2 ||А||). (13)
При т — п 2тг, оба метода имеют одинаковый порядок сложности 0(тп(3+1).
Если пользоваться быстрыми алгоритмами умножения целых чисел, то эти оценки можно улучшить пропорционально ускорению алгоритма умножения.
1. Gregory R.T., Krishnamurthy E.V. Methods and Applications of Error-Free Computation. Berlin, 1984.
2. Hurt M.F.,Waid C.A. A generalized inverse wicli give all the integral solutions to a sys-
tem of linear equations// SIAM J. Appl. Math. V. 10. 1970. P. 547-550.
3. Mulders T. and Storjohann A. Diophantine Linear System Solving// Proceedings of 1S-SAC’99: ACM International Symposium on Symbolic and Algebraic Computation. July 1999, Vancouver, Canada. P. 181-188.
4. Malaschonok G. Effective Matrix Methods in Commutative Domains// Formal Power Series and Algebraic Combinatorics/ Ed. by D. Krob, A.A. Mikhalev, A.V. Mikhalev. Springer, 2000. P. 506-517.
5. Coppersmith D. and Winogmd S. Matrix multiplication via arithmetic progressions// Journal of Symbolic Computation. 1990. V. 9. P. 251-280.
6. Dixon J. Exact solution of linear equations using p-adic expansions// Numer. Math. 1982. V. 40. P. 137-141.
7. Malaschonok G. Recursive Method for the Solution of systems of Linear Equations// Computational Mathematics/ Ed. by A. Sydow. Proceedings of the 15th IMACS World Congress. Berlin, 1997. V. 1. P. 475-480.
💥 Видео
Решение системы уравнений методом Крамера.Скачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом ГауссаСкачать

6 способов в одном видеоСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

Решение матричных уравненийСкачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

Решение систем уравнений методом подстановкиСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Как распознать талантливого математикаСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Матричный метод решения систем линейных уравнений (метод обратной матрицы)Скачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать