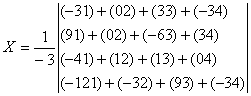Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
- Решение СЛАУ методом обратной матрицы
- Алгоритм решения
- Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.
- Решить систему линейных уравнений матричным методом
- Ввод данных в калькулятор для решения систем линейных уравнений матричным методом
- Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом
- 🌟 Видео
Видео:Решение матричных уравненийСкачать

Решение СЛАУ методом обратной матрицы
Напомним, что решением системы линейных уравнений называется всякая совокупность чисел <x1, x2, . xn> , подстановка которых в эту систему вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
Система линейных алгебраических уравнений обычно записывается как (для 3-х переменных):
| 2x1-3x2+x3 = 4 -x1+2x2+5x3 = 10 3x1-x2+3x3 = -1 | или | 2x-3y+z = 4 -z+2y+5z = 10 3x-y+3z = -1 |
См. также Решение матричных уравнений.</x
Видео:Матричный метод решения систем уравненийСкачать

Алгоритм решения
- Вычисляется определитель матрицы A . Если определитель равен нулю, то конец решения. Система имеет бесконечное множество решений.
- При определителе отличном от нуля, через алгебраические дополнения находится обратная матрица A -1 .
- Вектор решения X =<x1, x2, . xn> получается умножением обратной матрицы на вектор результата B .
Пример №1 . Найти решение системы матричным методом. Запишем матрицу в виде:
|
Вектор B:
B T = (3,-2,-1)
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆ = 2•(1•(-2)-2•0)-(-2•(3•(-2)-2•1))+1•(3•0-1•1) = -21
Итак, определитель -21 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Транспонированная матрица
| A T = |
|
Алгебраические дополнения.
| A1,1 = (-1) 1+1 |
| ∆1,1 = (1•(-2)-0•2) = -2 |
| A1,2 = (-1) 1+2 |
| ∆1,2 = -(3•(-2)-1•2) = 8 |
| A1,3 = (-1) 1+3 |
| ∆1,3 = (3•0-1•1) = -1 |
| A2,1 = (-1) 2+1 |
| ∆2,1 = -(-2•(-2)-0•1) = -4 |
| A2,2 = (-1) 2+2 |
| ∆2,2 = (2•(-2)-1•1) = -5 |
| A2,3 = (-1) 2+3 |
| ∆2,3 = -(2•0-1•(-2)) = -2 |
| A3,1 = (-1) 3+1 |
| ∆3,1 = (-2•2-1•1) = -5 |
| A3,2 = (-1) 3+2 |
| ∆3,2 = -(2•2-3•1) = -1 |
| A3,3 = (-1) 3+3 |
| ∆3,3 = (2•1-3•(-2)) = 8 |
Обратная матрица:
| A -1 = -1/21 |
|
Вектор результатов X = A -1 • B
|
X T = (1,0,1)
x1 = -21 / -21 = 1
x2 = 0 / -21 = 0
x3 = -21 / -21 = 1
Проверка:
2•1+3•0+1•1 = 3
-2•1+1•0+0•1 = -2
1•1+2•0+-2•1 = -1
Запишем матрицу в виде:
Вектор B:
B T = (1,2,3,4)
Главный определитель
Минор для (1,1):
= 3•(3•2-6•2)-5•(3•2-6•1)+7•(3•2-3•1) = 3
Определитель минора
∆ = 2•(-3)-3•0+5•3-4•3 = -3
Вектор результатов X
X = A -1 ∙ B
Пример №3 . Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
Решение:xls
Пример №4 . Записать систему уравнений в матричной форме и решить с помощью обратной матрицы.
Решение:xls
Пример №5 . Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления.
Методические рекомендации. После решения методом Крамера, найдите кнопку «Решение методом обратной матрицы для исходных данных». Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется.
Решение. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов:
|
Вектор B:
B T =(4,-3,-3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А -1 . Умножив обе части уравнения на А -1 , получим: А -1 *А*Х = А -1 *B, А -1 *А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А -1 .
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=-1•(-2•(-1)-1•1)-3•(3•(-1)-1•0)+2•(3•1-(-2•0))=14
Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
| A= |
|
Тогда:
| A=1/∆ |
|
где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1) i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
Транспонированная матрица
| A T = |
|
Вычисляем алгебраические дополнения.
| A1,1=(-1) 1+1 |
|
∆1,1=(-2•(-1)-1•1)=1
| A1,2=(-1) 1+2 |
|
∆1,2=-(3•(-1)-0•1)=3
| A1,3=(-1) 1+3 |
|
∆1,3=(3•1-0•(-2))=3
| A2,1=(-1) 2+1 |
|
∆2,1=-(3•(-1)-1•2)=5
| A2,2=(-1) 2+2 |
|
∆2,2=(-1•(-1)-0•2)=1
| A2,3=(-1) 2+3 |
|
∆2,3=-(-1•1-0•3)=1
| A3,1=(-1) 3+1 |
|
∆3,1=(3•1-(-2•2))=7
| A3,2=(-1) 3+2 |
|
∆3,2=-(-1•1-3•2)=7
| A3,3=(-1) 3+3 |
|
∆3,3=(-1•(-2)-3•3)=-7
Обратная матрица
| A -1 =1/14 |
|
Вектор результатов X
X=A -1 • B
|
| X=1/14 |
|
| X=1/14 |
|
X T =(-1,1,2)
x1= -14 / 14=-1
x2= 14 / 14=1
x3= 28 / 14=2
Проверка.
-1•-1+3•1+0•2=4
3•-1+-2•1+1•2=-3
2•-1+1•1+-1•2=-3
doc:xls
Ответ: -1,1,2.
Пример №6 . Решить неоднородную систему линейных алгебраических уравнений методом обратной матрицы.
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.
Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) матричным методом (методом обратной матрицы), вы сможете очень просто и быстро найти решение системы.
Воспользовавшись онлайн калькулятором для решения систем линейных уравнений матричным методом (методом обратной матрицы), вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Решить систему линейных уравнений матричным методом
Изменить названия переменных в системе
Заполните систему линейных уравнений:
Ввод данных в калькулятор для решения систем линейных уравнений матричным методом
- В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
- Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа.
- Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
- Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.
Например, линейное уравнение x 1 — 7 x 2 — x 4 = 2
будет вводится в калькулятор следующим образом:
Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом
- Между полями для ввода можно перемещаться нажимая клавиши «влево», «вправо», «вверх» и «вниз» на клавиатуре.
- Вместо x 1, x 2, . вы можете ввести свои названия переменных.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
🌟 Видео
Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Матрица интенсивностей. Система уравнений КолмогороваСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом ГауссаСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

ДУ Линейные системыСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Неоднородная система линейных уравненийСкачать

Система дифференциальных уравнений. Операционный методСкачать

Системы дифференциальных уравнений. Часть 2Скачать

Математика это не ИсламСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать