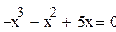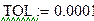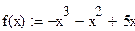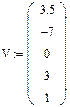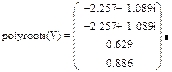В этом разделе приведены примеры решенных задач по теме нахождения корней нелинейных уравнений численными методами. На первом этапе обычно происходит локализация (отделение) корней (графически или аналитически), на втором — уточнение (поиск) корней разными методами: Ньютона, Стеффенсена, секущих, хорд, касательных, простой итерации.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Примеры приближенных решений нелинейных уравнений онлайн
Задача 1. Методом бисекции найти решение нелинейного уравнения на отрезке $[a;b]$ с точностью $varepsilon = 10^$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $varepsilon=10^$. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
Задача 2. Отделить корни нелинейного уравнения аналитически $2 arcctg x -x+3=0$.
Задача 3. Отделить корни нелинейного уравнения аналитически и уточнить один из них методом проб с точностью до 0,01. $$3x^4-8x^3-18x^2+2=0.$$
Задача 4. Отделить корни нелинейного уравнения графически (например, в среде EXCEL) уточнить один из них методом проб с точностью до 0,01. $$x^2-20 sin x =0.$$
Задача 5. Отделите корни уравнения графически и уточните один из них методом хорд с точностью до 0,001. Уточните один из корней этого уравнения методом касательных с точностью до 0,001. $$ sqrt — cos 0.387 x =0.$$
Задача 6.Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. $$sqrt=frac.$$
Задача 7. На отрезке $[0;2]$ методом Ньютона найти корень уравнения $-x^3-2x^2-4x+10=0$ с точностью 0,01.
Задача 8. Методом хорд найти отрицательный корень уравнения $x^3-2x^2-4x+7=0$ с точностью 0,0001. Требуется предварительное построение графика функции и отделение корней.
Задача 9. Решить нелинейные уравнения с точностью до 0.001. $$1), x^3-12x-5=0, (x gt 0), , 2), tan x -1/x=0. $$
Видео:ЧМ-1. Решение нелинейных уравнений. Часть 1/2Скачать
Изучение встроенных функций root(), polyroots(), Given-Find(). Решение системы нелинейных (линейных) уравнений
Страницы работы
Содержание работы
Лабораторная работа №4
— изучить встроенные функции root(), polyroots(), Given-Find().
— найти корни нелинейных уравнений с одной переменной.
— найти корни полинома.
— решить систему нелинейных уравнений.
— решить систему линейных уравнений.
Решить два нелинейных уравнения с точностью до 0,0001. Отобразить корни уравнений графически. Использоваться функцию root() двух форматов. Проверить корни полинома с помощью функции polyroots(). Подставить найденные корни в уравнения и оценить погрешность.
Установим точность вычисления, изменив значение переменной TOL:
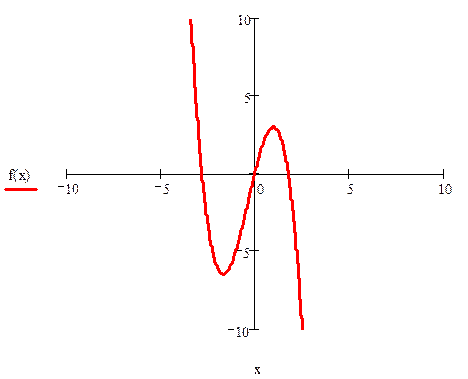
Построим график уравнения:
По графику видно, что у уравнения 3 корня.
Вычисление корней с помощью функции root() (1ый способ):
— определим саму функции
Для решения уравнения с помощью функции root() (1ый способ), нам необходимо задать начальное значение X, относительно которого будет выполняться поиск корня. Обратимся к графику, и установим эти значения.
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать
Решение уравнений с помощью функции root
Дата добавления: 2015-07-23 ; просмотров: 6798 ; Нарушение авторских прав
Функция root осуществляет решение алгебраических и трансцендентных уравнений, определяя вещественные корни уравнений. MathCAD в функции root использует для поиска корня метод секущих.
· f(x) – решаемое уравнений f(x);
· x – аргумент функции f(x) (искомое неизвестное уравнения).
При использовании функции rootзадаётся начальное приближение корня x0.
Функция root представляется в одной из следующих форм:
1-ый вариант 2-ой вариант 3-ий вариант
| x:=x0 | x:=x0 | x:=x0 |
| Root (f(x),x)= | z=root (f(x),x) | j(x):=f(x) |
| z= | z:=root(j(x),x) | |
| z= |
Если после многих итераций MathCAD не может найти решение, то появляется сообщение: «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:
- уравнение не имеет корней;
- корни уравнения расположены далеко от начального приближения;
- функция f(x) имеет локальные экстремумы между начальным приближением и корнем;
- функция f(x) имеет разрывы между начальным приближением и корнем;
- функция f(x) имеет комплексный корень, но начальное приближение было вещественным.
Чтобы установить причину ошибки рекомендуется построить график функции f(x). Он поможет выяснить наличие корней уравнения, определить начальные приближения.
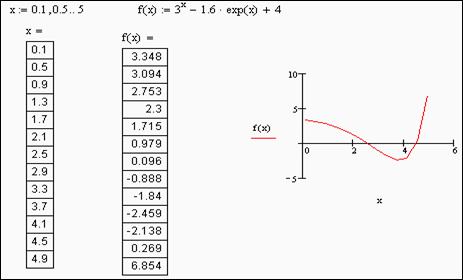
Пример 4.1. Решить уравнение: 3 X — 1.6*e X + 4=0.
Технология выполнения задания.
Определим количество корней уравнения и их интервалы изоляции. Для этого:
- задаём ранжированную переменную x=0.1,0.5..5 (примерный диапазон изменения) и заданное уравнение без правой его части (=0).
- Набираем x= (на экране появляется диапазон изменения x;)
- Набираем f(x)= (на экране появляется диапазон изменения заданного уравнения).
- В системе MathCAD выполнить команды View®Toolbars ® Graph. На появившейся панели Graph щёлкнуть по кнопке XY – Plot.
- Построить график заданного уравнения (см. рис. ).
- Определить по графику интервалы изоляции корней.
Построение графика заданного уравнения представлено на рис.4.1.
Рис. 4.1. График уравнения 3 Х – 1,6e X +4
По графику интервалы изоляции корней x1 и x2 соответственно равны: 2.5 Х – 1.6exp(x)+4,x)=2.541
root(3 Х – 1.6exp(x)+4,x)=4.473
Рис. 4.2. Решение уравнения 3 Х – 1,6*e X +4
Проверить правильность определения корней, подставив полученные решения в исходное уравнение.
Решение уравнений с помощью функции
ФункцияFindпредназначенадля решениясистемуравнений методом итераций. Как частный случай, функция может определять корни одного уравнения.
Решение уравнения выполняется в следующей последовательности:
- задать начальное приближение корня х0 из области его изоляции;
- написать слово Given, указывающее на то, что далее следует заданное уравнение;
- написать заданное уравнение. Следует иметь в виду, что при вводе в уравнение знака равенства необходимо нажать клавиши + ;
- написать функцию Find(x),гдеx –искомое неизвестное;
- нажать клавишу .(знак равенства).
Технология решения уравнения 3 Х — 1,6е Х +4 приведена на рис. 4.3.
| X:=2.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=2.541 | X:=4.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=4.472 |
Рис. 4.3. Решение уравнения 3 Х – 1,6e X +4
Определение корней многочлена с помощью функции polyroots
Корни многочлена обычно определяются с помощью функции polyroots, которая имеет вид:
где V – вектор коэффициентов многочлена, начиная с младшей степени.
Функция находит все вещественные и комплексные корни.
Технология решения задачи состоит в следующем:
- ввести символ присвоения имени вектора-столбца, например V:=;
- нажать комбинацию клавиш Ctrl+M. На экране появляется окно InsertMatrix.В полях Rows и Columns устанавливается число строк и число столбцов матрицы. Для случая определения корней полинома число столбцов равно 1, а число строк – (n+1), где n степень многочлена. После щелчка по кнопке ОК в окне, на экране появляется пустой шаблон вектора- столбца размером (n+1) ×1;
- заполнить маркеры ввода вектора коэффициентами заданного полинома, в первой строке пишется коэффициент свободного члена (коэффициент при нулевой степени полинома);
- написать polyroots (V);
- нажать клавишу = (равно) на клавиатуре. На экране появится ответ в виде вектора корней.
Пример 4.2.Решить уравнениеx 4 +3x 3 -7x+3.5=0
Технология выполнения задания приведена на рис. 4.4.
Рис. 4.4. Решение уравненияx 4 +3x 3 -7x+3.5=0.
Возьмите из Задания 4.1 и Задания 4.2 свой вариант уравнения и найдите его корни используя функцию root и функцию polyroots. Убедитесь, что найденные значения действительно являются корнями Вашего уравнения.
Задание 4.1. Найти все корни заданного уравнения, используя функцию root
| №п.п. | Уравнение f(x) | № п.п. | Уравнение f(x) |
| 4sin x + x 2 — 2=0 | (x — 1) 2 — 0.5exp( — x) – 2=0 | ||
| 3 X -4.5x-5.6=0 | 2/x+x 2 + e x – 8=0 | ||
| 3 sinÖx +0.35x-8x=0 | tgx + x + 2=0 | ||
| 0.25x 2 +x-1.25002=0 | ctgx – 2x + 2=0 | ||
| 0.1x 2 -xlnx=0 | -x 2 + cos (x+1) + 3=0 | ||
| 3x — 4lnx-5=0 | 2ln(2–x)–x + e x – 10=0 | ||
| e x — e –x -2=0 | 1/x + ln(2x + 4) – 3=0 | ||
| e x + lnx – 10x=0 | x× cos x + 1.5=0 | ||
| sin x 2 +cos x 2 -10x=0 | 2x 5 – lnx – 7x 2 =0 | ||
| x 2 -ln(1+x)-3=0 | x×sinx x + 1.5=0 | ||
| 2xsin x – cosx=0 | x2 x – 4x 2 + 1.5=0 | ||
| lnx – x + 1.8=0 | 2.5 x – 8.6x – 3.5=0 | ||
| 0.6 ×3 x – 2.3x – 3=0 | ln(x + 2) + 2x 2 — 9x + 2=0 | ||
| 2 x – 4x=0 | xln(2.5x) – 1.5x + 1.5=0 | ||
| 3x – e x + 4=0 | xtgx – 1/3=0 |
Задание 4.2. Найти все корни заданного уравнения, используя функцию polyroots
Для полинома g(x) выполнить следующие действия:
1. с помощью команды Symbolics ® Polynomial Coefficients (Коэффициенты полинома)создать вектор V, содержащий коэффициенты полинома;
2. решить уравнение g(x) = 0 с помощью функции polyroots;
3. решить уравнение символьно, используя команду Symbolics ® Variable ®Solve
📸 Видео
Графический способ решения систем уравнений. Алгебра, 9 классСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Как найти корни уравнения в Excel с помощью Подбора параметраСкачать
Метод касательных для приближённого решения алгебраических уравненийСкачать
8 класс, 21 урок, Графическое решение уравненийСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Mathcad-09. Пример: уравненияСкачать
14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Графический метод решения задачи линейного программирования (ЗЛП)Скачать
Способы решения систем нелинейных уравнений. 9 класс.Скачать
СЛОЖИТЕ ДВА КОРНЯСкачать
1,2 Решение нелинейных уравнений методом хордСкачать
Решение нелинейных уравнений методом хордСкачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Графический метод решения уравнений 8 классСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Mathcad Prime. Урок 5 - Способы решения уравненийСкачать
