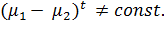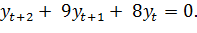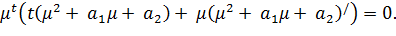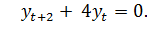- Разностные уравнения для чайников
- Примеры решений разностных уравнений
- Помощь с разностными уравнениями
- Разностные уравнения
- Разностные уравнения
- Разностные уравнения первого порядка с постоянными коэффициентами
- Разностные уравнения второго порядка с постоянными коэффициентами
- Линейные неоднородные стационарные разностные уравнения второго порядка
- 🎦 Видео
Видео:6.3 Решение разностных уравненийСкачать

Разностные уравнения для чайников
На этой странице мы рассмотрим примеры решения типовых задач, встречающихся в курсе дифференциальных и разностных уравнений, а именно нахождение общего или частного решения линейного разностного уравнения с постоянными коэффициентами. Чаще всего в контрольных встречаются уравнения второго или третьего порядка:
$$ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)=f(x), \ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)+ a_3 y(x+3)=f(x). $$
Здесь $a_i$ — постоянные коэффициенты, $f(x)$ — правая часть (неоднородность уравнения), $y(x)$ — искомая неизвестная функция.
Решение разностных уравнений практически полностью аналогично решению линейных дифференциальных уравнений с постоянными коэффициентами (см. тут примеры): ищется решение однородного уравнения через составление характеристического уравнения, и частное решение неоднородного уравнения по виду правой части.
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Примеры решений разностных уравнений
Задача 1. Решить разностное уравнение: $y(x+2)-4y(x+1)+4y(x)=2^x$
Задача 2. Найти общее решение линейного разностного неоднородного уравнения второго порядка с постоянными коэффициентами.
Задача 3. Решить разностное уравнение третьего порядка
$$ y(x+3)-16y(x+2)+83y(x+1)-140y(x)=0, quad y(0)=3, y(1)=18, y(2)=120. $$
Задача 4. Найти частное решение однородного разностного уравнения:
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Помощь с разностными уравнениями
Если вам нужна помощь с решением задач и контрольных по дифференциальным и разностным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Разностные уравнения
Содержание:
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Разностные уравнения
Понятие разницы и разностного уравнения
Если для значений переменной x1, x2, x3, . функция f (x) принимает значения f (x1), f (x2), f (x3) . , то приращения функции составляют f (x2) – f (x1), f (x3) – f (x2), .
Приращение функции при переходе от значения xi к значению xi+1 будем обозначать: 

Введем обозначения ΔΔf (x) = Δ 2 f (x), тогда Δ 2 f (x) = f (x + 2) — 2 f (x + 1) + f (x) и называется разностью второго порядка.
Аналогично можно найти разности третьего, четвертого и т. д. порядков.
Определим разности некоторых важнейших функций.
1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.
Понятно, что и все разности следующих порядков будут также равняться нулю.
2) Если f (x) = ax + b, то
Δf = Δf (x + 1) — f (x) = a (x + 1) + b — ax — b = a.
Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.
3) Если f (x) = ax 2 + bx + c, то 
Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.
4) Если f (x) = a x , то 
В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.
Обозначим yt — значение функции y в момент времени t; yt+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., yt+2 — значение функции y в момент, сдвинутый на две единицы и т. д.
Очевидно, что
Откуда:
За разность второго порядка, имеем 

поэтому
Аналогично можно доказать, что
Итак, любую функцию 
можно представить в виде: 
и наоборот.
Определение. Уравнение

называется разностным уравнением n-го порядка.
Решить разностное уравнение n-го порядка — это значит найти такую функцию yt, которая превращает уравнение (7.50) или (7.51) в тождество.
Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.
Определение. Уравнение

где a0, a1, . an — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.
Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:

Уравнение 

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y1 (t) и y2 (t), то его решением будет также функция y1 (t) + y2 (t).
ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.
ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A1, A2, . An) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A1, A2, . An).
Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.
Разностные уравнения первого порядка с постоянными коэффициентами
Рассмотрим неоднородное разностное уравнение

Соответствующее ему однородное уравнение будет:

Возьмем функцию 



Итак, 
По теореме (2) общее решение однородного разностного уравнения (7.55) является функция 
Пусть 

Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если 

Итак, общее решение уравнения (7.54) запишем в виде: 
Разностные уравнения второго порядка с постоянными коэффициентами
Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:

и соответствующее ему однородное уравнение

Убедимся, что функция 


Это уравнение называется характеристическим уравнением для уравнения (7.57).
Здесь могут иметь место следующие три случая:
1. D = a 2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде: 
а общее решение неоднородного уравнения (7.56) запишется так:
2. D = a 2 – 4b = 0, тогда 

В этом случае однородное уравнение (7.57) примет вид:

Тогда 
Легко убедиться, что решением уравнения (7.59) является также функция


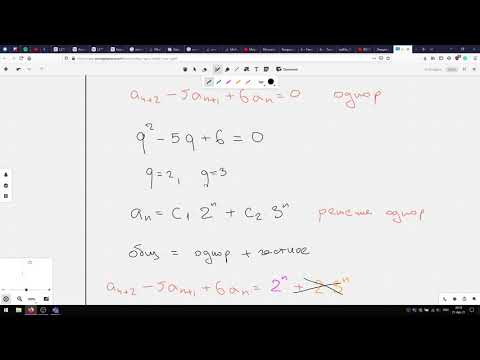
3. D = a 2 – 4b 2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция 
Далее положим, что yt = y — частное решение неоднородного уравнения, тогда 
Таким образом, общим решением неоднородного уравнения является функция 

Решим эту систему уравнений относительно A1 и A2:
Откуда
Итак, 
Примеры применения разностных уравнений в экономических задачах
Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:


Если положить y0 = F , то A = F, откуда
Это известная формула величины фонда F, который выдается под сложный процент.
Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года 

Цена равновесия для данной продукции определяется равенством:

Положим, что функция спроса определяется формулой 
Цена равновесия запишется: 


Тогда p0 = A и решением уравнения является функция 
Если начальная цена p0 = 0, то pt = 0 для всех значений t.
Следовательно, цена не подлежит изменению.
Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Математика без Ху!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.Скачать

Линейные неоднородные стационарные разностные уравнения второго порядка
Лекция № 3. Разностные уравнения
1. Основные понятия теории разностных уравнений.
2. Стационарные разностные уравнения первого порядка.
3. Линейные однородные стационарные разностные уравнения второго порядка.
4. Линейные неоднородные СРУ второго порядка.
5. Нестационарные линейные разностные уравнения первого порядка.
Литература
1. Романко В.К. Разностные уравнения. – М.: Бином, 2006.
Основные понятия теории разностных уравнений
Функция 


Построим приращения этой функции при переходе из точки 




В экономических исследованиях нередко встречаются задачи, в которых роль независимой переменной играет время t, а значения функции фиксируются через равные промежутки времени (1 час, 1 день, 1 месяц, 1 год и т.п.).
Например, так называемая «паутинообразная» модель рынка одного товара описывается уравнением

где 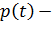

При моделировании относительной численности какого-либо биологического вида появляется уравнение вида

где 

По аналогии с (1) построим приращения значений функции




Из системы (4) следует


Из определения второй разности следует, что













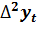

Используя метод математической индукции, можно доказать, что




Поэтому каждую функцию
можно представить как функцию

Определение.



называетсяразностным уравнением n-го порядка.
Определение.
Решить разностное уравнение n-го порядка – значит найти функцию 
Стационарные разностные уравнения первого порядка
Определение.
называется неоднородным стационарным разностным уравнением первого порядка.
Если 
Обозначим 

Убедимся в том, что функция 




Отсюда следует, что любая функция вида 
Итак, 
Теорема.Если 



Пример.

Пусть 

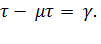


Линейные однородные стационарные разностные уравнения второго порядка
Определение.
Линейным разностным стационарным уравнением порядка nназывается уравнение вида
где 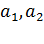

Такие уравнения являются наиболее важными для практики.
Определение.
Если 
Очевидно, такое уравнение всегда имеет решение
Будем рассматривать линейные разностные стационарные уравнения второго порядка:


Соответствующее однородное уравнение имеет вид:


Нетривиальное решение уравнения (2) будем искать в виде

Для нахождения 




Так как 

которое не имеет нулевых корней.
Уравнение (3) называется характеристическим уравнением для уравнения (2).
Таким образом, 

Возможны три случая:
1. Дискриминант 
Тогда функции 

Теорема 1.
Если 


его решение для любых
Доказательство следует из линейности уравнения (2). Итак, в данном случае,


Пример.
Решить уравнение


имеет два различных действительных корня

2. D = 0. Характеристическое уравнение имеет один двукратный действительный корень: 


(t + 2) 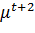


=
=
Функции 


Отсюда следует, что решение уравнения (2) имеет вид:

Пример.
Решим уравнение


Имеет двукратный действительный корень 
3. D 

Теорема.
Функция 

Примечание: Real — действительный, Imagine – мнимый.
Доказательство следует из линейности (2).
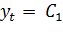

Пример.
Найдём общее решение уравнения
Характеристическое уравнение 
Общее комплексное решение имеет вид

Так как 


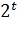

Общее решение однородного разностного стационарного уравнения.
Линейные неоднородные стационарные разностные уравнения второго порядка
Теорема.
Если 



Пример.
Решим уравнение 
Общее решение соответствующего ему однородного уравнения найдено выше. Предположим, что частное решение данного неоднородного уравнения имеет вид:

Тогда



🎦 Видео
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Дифференциальные и разностные уравнения. Л.16. Линейные разностные уравнения. Н.А. ХохловСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

21.04 - дискра, рекуррентные соотношенияСкачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Разностное функциональное уравнение решено двумя способами.Скачать