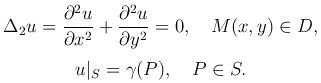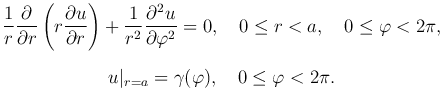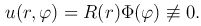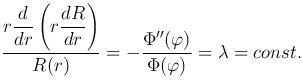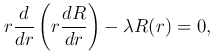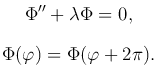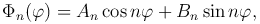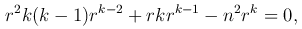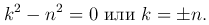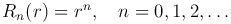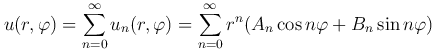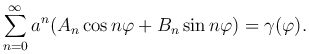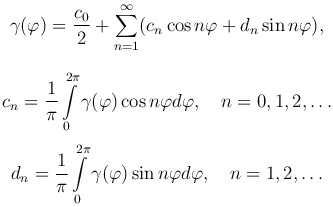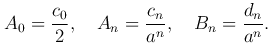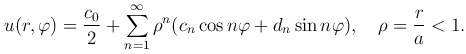Решить краевую задачу дирихле для уравнения лапласа в круге

Рассмотрим внутреннюю краевую задачу для уравнения Лапласа с граничным условием первого рода

Пусть область D — круг радиуса a, ограниченный окружностью S. Это есть задача Дирихле в круге.

Запишем данную задачу в полярных координатах:

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Решение этой задачи будем искать методом разделения переменных в виде

Подставляя это выражение в уравнение Лапласа и разделяя переменные, получаем

Следовательно, функция R(r) должна быть найдена из решения уравнения

а для функции Φ(φ) получаем задачу на собственные значения

Здесь условие периодичности функции Φ(φ) является следствием периодичности искомого решения u(r, φ) по угловой переменной φ с периодом 2π.

Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

Последняя задача имеет нетривиальные периодические решения только при λ=&lambda_n=n², n=0, 1, 2, … Эти решения имеют вид

Для функции R(r) при λ=n² получаем уравнение

()

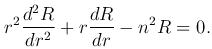
Будем искать частные решения этого уравнения в виде степенной функции

тогда последнее уравнение примет вид

устанавливаем, что показатель k определяется из уравнения

Следовательно, уравнение () имеет два линейно независимых решения: r n и r -n .

Видео:Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

Решение внутренней задачи Дирихле должно быть ограничено в центре круга при r=0. Поэтому из двух найденных решений следует взять лишь

Таким образом, частные решения уравнения Лапласа в полярных координатах можно записать так:

В силу линейности и однородности равнения Лапласа суперпозиция частных решений

также будет удовлетворять этому уравнению.

Из граничного условия получим:

Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

Разложим функцию γ(φ) в интервале (0, 2π) в тригонометрический ряд Фурье:

Приравняв коэффициенты в двух рядах, находим

Тогда решение можно записать в форме

Замечание. Если в этой формуле считать ρ=a/r>1, то она будет определять решение внешней для круга задачи Дирихле.

Решение задачи Дирихле для круга методом Фурье

Видео:Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать

По этой ссылке вы найдёте полный курс лекций по математике:

Задача ставится так: найти функцию tx(r,у?), удовлетворяющую внутри ируга Kr0 радиуса с центром в начале координат уравнению Лапласа непрерывную в замжутой области KtQ и принимающую задан ные значения награнице круга, Решение задачи Дирихле для круга методом Фурье где f(tp) — достаточно гладкая функция, периодическая с периодом 2т.

В силу однозначности искомого решения оно должно быть периодическим по с периодом Из непрерывности решения в Кго следует его ограниченность в КГо. Уравнение (1) в полярных координатах имеет вид (3) Будем искать частные решения уравнения (3) в виде . Подставляя «(г, (р) в форме (4) в уравнение (3),умноженное на г2, получим откуда Из условия получаем находим , так что В частности, = Ао = const. Полагая в уравнении (6) (уравнении Эйлера) Л(г) = г*, при А = п2 получаем Отсюда) и, следовательно.

При п = 0 из (6) находам Так как ооприг 0+0,тодля решения внутренней задачи Дирихле нужно положить Решение внутренней задачи Дирихле будем искать в виде ряда (5) (6) где коэффициенты Ап, Вп определяются из граничного условия (2) При т — tq имеем Запишем разложение /(у) в ряд Фурье где Решение задачи Дирихле для круга методом Фурье Сравнивая ряды (8) и (9), получаем (9) * г0 г0.

Таким образом, формальное решение внутренней задачи Дирихле для круга предста-вимо в виде ряда оо где коэффициенты определяются по формулам (10).

Возможно вам будут полезны данные страницы:

При г го ряд (11) можно дифференцировать по г и любое число раз, и, значит, функция u(r, у) из (11) удовлетворяет уравнению Если предположить, что функция непрерывна и дифференцируема, то ряд (11) при г ^ г0 сходится равномерно, и, следовательно, функция и(г, непрерывна на границе круга и удовлетворяет всем условиям поставл енной задачи.

искать в виде ряда где коэффициенты Ап, В„ определяются из граничного условия Для кольцевой области образованной двумя концентрическими окружностями с центром в точке 0 радиусов Г] и г2 (рис.8), решение задачи ищется в виде ряда коэффициенты которого Л0, определяются из граничных условий Пример.

Видео:Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

Найти функцию, гармоническую внутри круга радиуса го с центром в начале координат и такую. что Решение задачи Дирихле для круга методом Фурье -4 Задача сводится к решению внутренней задачи Дирихле для уравнения при граничном условии Будем искать решение задачи в вида ряда ПО Из граничного условия (15) имеем Отсюда в силу ортогональности системы функций Искомое решение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

🎥 Видео

Часть 1. Примеры на краевую задачу Лапласа в кругеСкачать

OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 5. Уравнение Лапласа в полярных коорд. 1Скачать

Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать

УМФ, 24.11, уравнение Лапласа в кругеСкачать

7.1 Решение уравнения Лапласа в прямоугольникеСкачать

15. Решение уравнения теплопроводности в кругеСкачать

Решение начально-краевых задач в круге для волнового уравнения и теплопроводностиСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 8. Задача Штурма-Лиувилля в пол. коорд. 1Скачать

7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать

Колыбасова В.В. - Методы математической физики.Семинары - 14. Уравнение Лапласа в цилиндреСкачать

Задача Дирихле для шараСкачать

Решение уравнения Лапласа в шареСкачать

Шапошникова Т. А. - Уравнения с частными производными. Часть 1. Семинары - Семинар 10Скачать