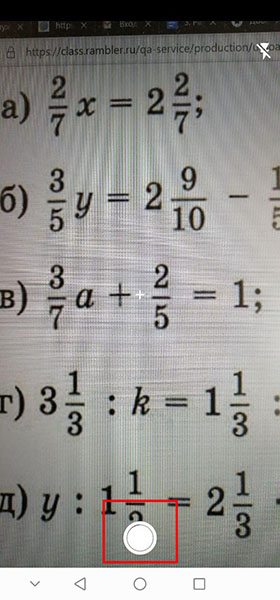Решить иррациональное уравнение по фото

Один из элементов математики — это уравнения. Они встречаются на всех этапах: от начальной алгебры до высшей математики, а также применяются и в других науках. Уравнения являются основной многих теорий в разнообразных дисциплинах. Поэтому решать их учат уже в школе, и с каждым классом они становятся всё сложнее, и сложнее.

Решать их не всем по зубам. Даже имея понятное объяснение в учебнике и квалифицированного педагога, перед определёнными примерами некоторые ученики оказываются в тупике. Поэтому в данной статье мы рассмотрим решение простых и сложных уравнений по фотографии в режиме онлайн. Расскажем о способах, которые легко и качественно помогут определить неизвестные числа любого примера.

Однако, всё же, рекомендуем использовать описанные приложения не для получения решения задач, а для проверки своей работы, чтобы убедиться, что она решена правильно. Ведь упражнения, которые вам задают выполнить в учебном заведении, понадобится вам в будущем на контрольных работах и экзаменах, и важно научиться решать их самому, ведь доступа к смартфону у вас, возможно, не будет.

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Математический онлайн-сканер по фото

Одно из самых качественных приложений подобного рода, заслужило хорошее оценку пользователей и имеет большое количество скачиваний. Подойдёт для устройств под управлением Android.

К функциям и достоинствам этого инструмента можно отнести следующее:

• Умеет решать как простые, так и сложные уравнения.
• Ему под силу не только уравнения, но и многие другие математические задачи.
• Воспринимает задачи по фото — достаточно навести камеру и сфотографировать.
• Уравнение можно ввести числами в калькулятор уравнений.
• Пошагово расписывает решение уравнения, а не только даёт конечный ответ.
• Имеет встроенные простой и тригонометрические калькуляторы.
• Есть множество дополнительных утилит для разных задач, не только по математике, но и тригонометрии, химии, физике и другим наукам.
• Абсолютно бесплатно и минимум рекламы.

Присутствуют и недостатки — интерфейс только на английском языке . Однако большинство задач можно решить и не зная языка. Поэтому этот минус можно легко нивелировать.

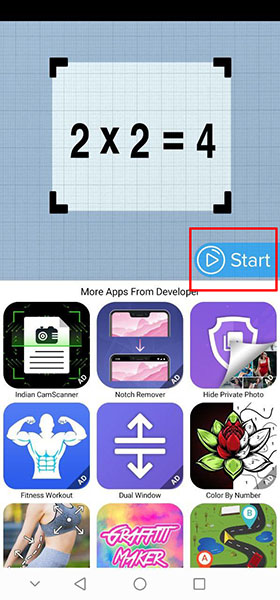
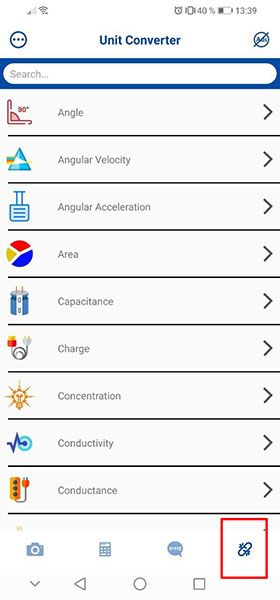
Итак, скачайте приложение для Android можно из Google Play. После установки и запуска нажмите кнопку « Start «.

Перед вами сразу появится камера, готовая к фотографированию уравнения, которое вы не можете решить. Наведите объектив на уравнение, чтобы оно целиком попало в квадрат с синей границей, и нажмите на круглую кнопку снизу, чтобы фотографировать. С помощью перетаскивания вы можете менять границы.

После анализа фото появится версия распознанного уравнения. Здесь желательно проверить, правильно ли приложение распознало все числа и знаки. Если не правильно, то нужно переделать фото, иначе решение получится некорректным. А если правильно, то можно нажать на « Solve «.

Через пару мгновений вы увидите пошаговое решение этого уравнения и итоговый ответ к нему. Желательно проверить решение самому, прежде, чем применять его.

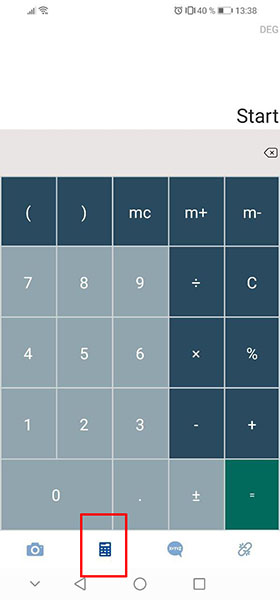
Внизу вы увидите иконки с вкладками с дополнительными функциями, которые тоже могут быть вам полезны. Первая кнопка — это фото-сканер уравнений, который был описан выше. А вторая — калькулятор чисел.

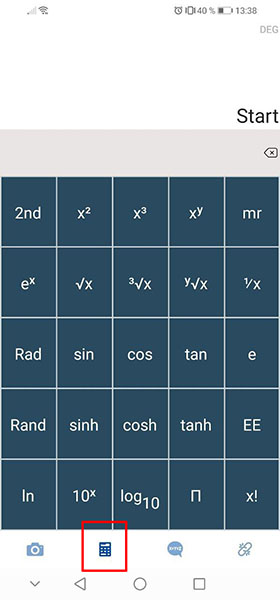
Жестом вверх можно открыть тригонометрический калькулятор.

Третья кнопка — калькулятор уравнений, который поможет их решить.

И четвёртая — дополнительные утилиты.

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Mathway — приложение для быстрого решения уравнений

Замечательное приложение, которое справляется с поставленной задачей не хуже, чем предыдущее. Имеются версии для iOs и Android. Это условно-бесплатная программа, и главный недостаток бесплатной версии — отсутствие шагов решения. То есть приложение выдаст только результат с кратким ходом решения. Но этого может вполне хватить для того, чтобы сверить правильность своего ответа на уравнение.

Вот какие функции и возможности имеются:

• В платной версии есть пошаговые решения и отсутствует реклама. В бесплатной — краткое решение и итоговый ответ, есть немного рекламы. А пошаговое присутствует только в некоторых простых задачах.
• Умеет решать задачи широкого спектра — от начальной алгебры до высшей математики, включая химические задачи, а также построение графиков и многое другое.
• Уравнение для решения можно ввести как онлайн через фото, так и вручную.
• Предлагается несколько методов решения уравнений, если это возможно.
• Присутствует русский язык.

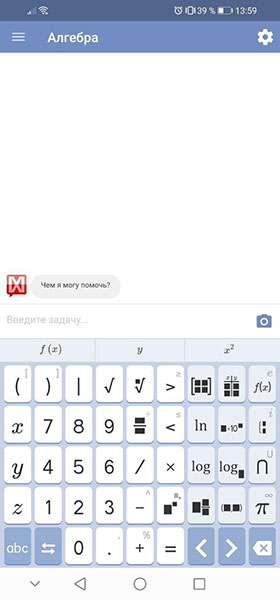
Скачать Mathway можно из официальных магазинов приложений для Android и iOs. После запуска вы увидите страницу, похожую на чат.

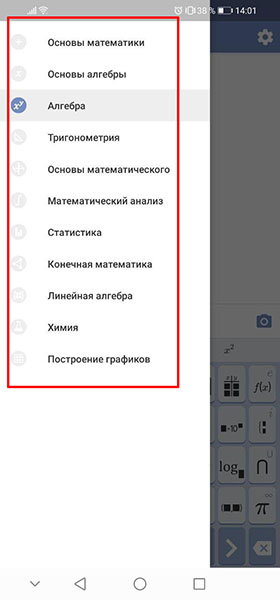
Первым делом здесь следует нажать на три линии вверху слева, чтобы открыть меню задач. В них вы можете познакомиться со всем спектром алгоритмов и выбрать область уравнений, которые сейчас хотите решить по фотографии.

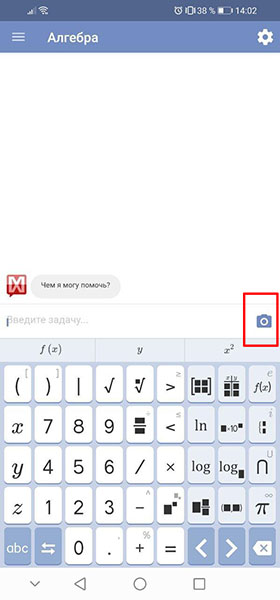
Выберите нужную область задач, а затем загрузите само уравнение в приложение онлайн. Сделать это можно как вручную с помощью клавиатуры, так и через фото. Чтобы сделать решение, в поле ввода нажмите на иконку в виде фотоаппарата.

Откроется камера. Наведите объектив на уравнение так, чтобы оно оказалось в центре экрана и нажмите на белую кнопку, чтобы сфотографировать.

После этого вам нужно будет с помощью границ отметить то уравнение, которое вы хотите решить по фото. Если сфотографировалось несколько задач, то выделить нужно только одну. Двигать границы можно жестом перетаскивания. Когда всё будет готов, нажмите на иконку в виде самолётика внизу.

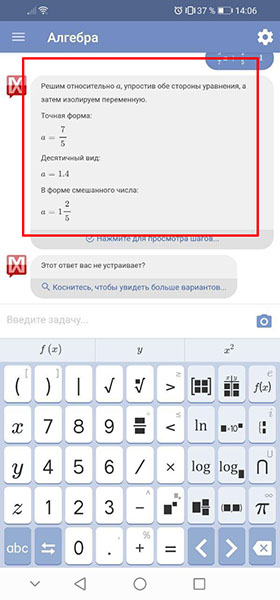
Если заданное вами уравнение можно решить несколькими методами, то вам будет предложен выбор метода. Если только одним, то вы сразу получите ответ. Также для некоторых простых уравнений может быть предложено и пошаговое решение даже в бесплатной версии.

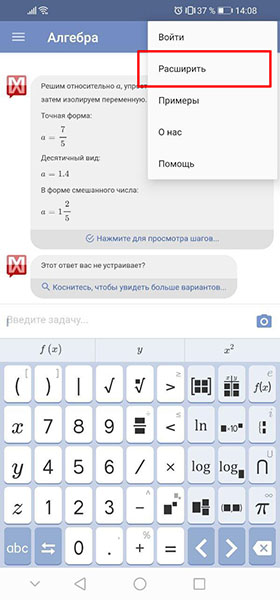
Если вы хотите приобрести платную версию Mathway, то нажмите на шестерёнку вверху справа, а потом « Расширить «.

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Photomath — поможет разгадать математическую задачу по фото

Замечательное приложение с высокой оценкой пользователей, хорошими отзывами, русским языком и пошаговыми решениями. Полностью бесплатный инструмент, в котором нет ни одной рекламы, а также есть версии для Android и iOs. У Photomath есть официальный сайт https://photomath.com/ru/, на котором можно более подробно ознакомиться с ним.

К функциями и достоинства Photomath можно отнести следующие аспекты:

• Решение любых уравнений по фотографии прямо в онлайн режиме может проходить по нескольким методам, если это возможно.
• Показывает ход решения и итоговый ответ.
• Можно ввести задачу как с помощью фото методом сканирования, так и вручную через клавиатуру.
• Хранит историю решений.
• Присутствует русский и многие другие языки.

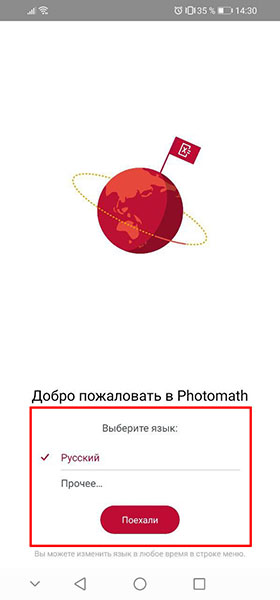
Итак, чтобы начать пользоваться Photomath, установите его на своё устройства под управлением iOs или Android, и запустите. Вам понадобится выбрать желаемый язык, а потом нажмите « Поехали «.

Затем появится презентация работы программы, которую вы можете либо просмотреть, либо нажать « Пропустить «.

После этого откроется камера. Вам нужно навести объектив на уравнение так, чтобы оно оказалось в красной рамке. Вы можете двигать границы касанием. Когда уравнение окажется в прямоугольнике, нажмите на красную кнопку снизу, чтобы распознать его для решения.

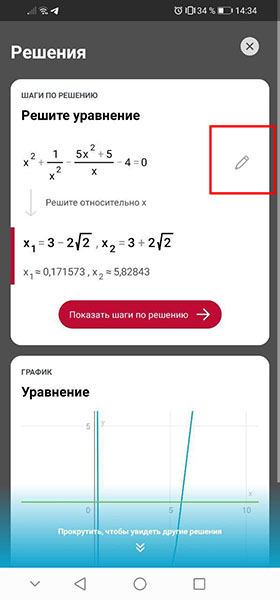
Через пару мгновений вы увидите решение и ответ. Если методов решения может быть несколько, то будут приведены все возможные варианты. Например, уравнение из этого примера можно решить ещё и графиком и он тоже есть. Вы можете нажать на иконку в виде карандаша, чтобы отредактированы распознанную задачу, если приложение сделало это неверно.

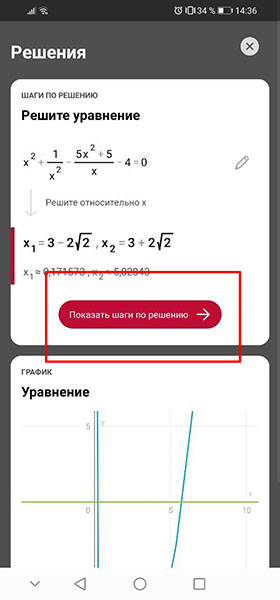
Нажмите « Показать шаги по решения «, чтобы увидеть более подробно.

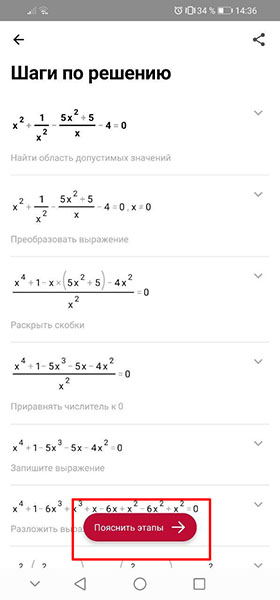
Если вам нужно ещё подробнее, то нажмите « Пояснить этапы «.

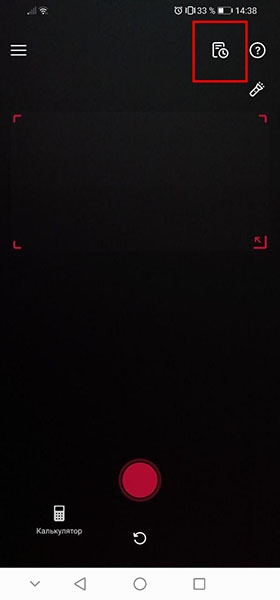
Кроме этого можно открыть историю всех решений, которые проводились ранее. Для этого нужно нажать на кнопку вверху справа на начальной странице.

А калькулятор можно открыть с помощью кнопки внизу слева.

Итак, выше были рассмотрены приложения, которые по фотографии могут решать уравнения, и у всех примерно одинаковый алгоритм работы.

Перед использованием этих инструментов вам следует помнить о некоторых вещах:

• Правильность ответа зависит от качества фото, поэтому старайтесь фотографировать уравнения в хорошем свете и так, чтобы в объективе было только одно уравнение.
• Распознавать лучше напечатанные уравнения, чем рукописные.
• После распознавания проверяйте правильность цифр и знаков.
• После получения результата проверяйте его.

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Решение уравнений по фотографии — приложения для математиков

Как же часто школьникам и студентам не удается решить сложные математические примеры!

Даже если задания легкие, но их слишком много, хочется, чтобы их сделал кто-то другой. Решение существует — решение уравнений по фотографии.

Принцип их работы прост: фотографируете пример, загружаете фото в программу (чаще всего в подобных приложениях уже есть встроенная камера), и она выдает пошаговое решение. Читайте до конца и узнавайте об этих программах, которые не только найдут правильное решение для всех примеров, но и научат вас делать то же самое!

Видео:Иррациональные уравнения | Математика ЕГЭ 10 класс | УмскулСкачать

Решение уравнений по фотографии: Photomath

Пожалуй, самым популярным и распространенным математическим приложением является Photomath. Приведем небольшую инструкцию по работе с этой программой:

• Photomath уже имеет встроенную камеру. Вы наводите ее на пример, и приложение начинает его анализ;
• если схемы решения данного задания уже заложены в «мозг» приложения, то оно выдает решение;
• решение разделено на несколько этапов, есть промежуточные результаты. Каждый шаг можно отдельно изучить;
• немаловажный плюс — с построением графиков программа также справляется.

Видео:Иррациональное уравнение на 2 минутыСкачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Иррациональные уравнения #1Скачать

Калькулятор онлайн.
Решение иррациональных уравнений и неравенств.

Этот математический калькулятор онлайн поможет вам решить иррациональное уравнение или неравенство. Программа для решения иррациональных уравнений и неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> sqrt(x) — квадратный корень x
x^(1/n) — корень степени n

Введите иррациональное уравнение или неравенство
Решить уравнение или неравенство

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Немного теории.

Видео:✓ Иррациональное уравнение | ЕГЭ-2018. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать

Решение иррациональных уравнений и неравенств

Видео:Иррациональное уравнениеСкачать

1. Иррациональные уравнения

Иррациональными называют уравнения, в которых переменная содержится под знаком радикала или под знаком возведения в дробную степень. Для таких уравнений ищут, как правило, только действительные корни.

Основной метод решения иррациональных уравнений — метод возведения обеих частей уравнения в одну и ту же степень. При этом следует иметь в виду, что возведение обеих частей уравнения в одну и ту же нечётную степень есть равносильное преобразование уравнения, а в чётную — НЕравносильное. Значит, основные принципиальные трудности связаны с возведением обеих частей уравнения в одну и ту же чётную степень, когда из-за неравносильности преобразования могут появиться посторонние корни, а потому обязательна проверка всех найденных корней.

ПРИМЕР 1.
( sqrt[Large6normalsize] = sqrt[Large6normalsize] )

Возведя обе части уравнения в шестую степень, получим:
( x^2-5x = 2x-6 Rightarrow )
( x^2-7x +6= 0 Rightarrow )
( x_1=1, ; x_2=6 )
Проверка. «Хорошие» корни можно проверить непосредственной подстановкой в исходное уравнение. При x = 1 заданное уравнение принимает вид ( sqrt[Large6normalsize] = sqrt[Large6normalsize] ), во множестве действительных чисел такое «равенство» не имеет смысла. Значит, 1 — посторонний корень, он появился по причине расширения ОДЗ уравнения после возведения в шестую степень. При х = 6 заданное уравнение принимает вид ( sqrt[Large6normalsize] = sqrt[Large6normalsize] ) — это верное равенство.
Итак, уравнение имеет единственный корень: х = 6.
Ответ: х = 6

Введя новую переменную ( u=x^2-x), получим существенно более простое иррациональное уравнение:
( sqrt+sqrt = sqrt ).
Возведём обе части уравнения в квадрат:
( (sqrt+sqrt)^2 = (sqrt)^2 Rightarrow )
( u+2 +2sqrtsqrt +u+7 = 2u+21 Rightarrow )
( sqrt = 6 Rightarrow )
( u^2+9u+14=36 Rightarrow )
( u^2+9u-22=0 Rightarrow )
( u_1=2, ; u_2=-11 )
Проверка найденных значений их подстановкой в уравнение ( sqrt+sqrt = sqrt ) показывает, что ( u_1=2 ) — корень уравнения, а ( u_2=-11 ) — посторонний корень.
Возвращаясь к исходной переменной x, получаем уравнение ( x^2-x=2 Rightarrow x^2-x-2=0 ), решив которое находим два корня: ( x_1=2, ; x_2=-1 )
Ответ: 2; -1.

Уединение корня и возведение обеих частей уравнения в квадрат привело бы к громоздкому уравнению. В то же время, если проявить некоторую наблюдательность, можно заметить, что уравнение легко сводится к квадратному. Действительно, умножим обе его части на 2:
( 2x^2 +6 -2sqrt = 3x+12 Rightarrow )
( 2x^2 -3x +2 -2sqrt -8 = 0 Rightarrow )

Введя новую переменную ( y=sqrt ), получим: ( y^2-2y-8=0 ), откуда ( y_1=4, ; y_2=-2 ). Значит, исходное уравнение равносильно следующей совокупности уравнений:
( left[begin sqrt =4 \ sqrt = -2 endright. )

Из первого уравнения этой совокупности находим: ( x_1=35; ; x_2=-2 ). Второе уравнение корней не имеет.

Проверка. Так как совокупность уравнений равносильна исходному уравнению, причём второе уравнение этой совокупности корней не имеет, то найденные корни можно проверить подстановкой в уравнение ( sqrt =4). Эта подстановка показывает, что оба найденных значения x являются корнями этого уравнения, а значит, и исходного уравнения.
Ответ: 3,5; -2.

Областью определения уравнения является луч ( [5; ; +infty) ). В этой области выражение ( sqrt ) можно представить следующим образом: ( sqrt = sqrtsqrt ). Теперь уравнение можно переписать так:
( x+x -5 +2sqrtsqrt +2sqrt +2sqrt -48 = 0 Rightarrow ) ( (sqrt)^2 +2sqrtsqrt +(sqrt)^2 +2(sqrt+sqrt) -48 = 0 Rightarrow ) ( (sqrt +sqrt)^2 +2(sqrt+sqrt) -48 = 0 )

Введя новую переменную ( y= sqrt +sqrt ), получим квадратное уравнение ( y^2+2y-48=0 ), из которого находим: ( y_1=6, ; y_2=-8 ). Таким образом, задача свелась к решению совокупности уравнений:
( left[begin sqrt +sqrt =6 \ sqrt +sqrt = -8 endright. )
Из первого уравнения совокупности находим ( x= left( frac right)^2 ), второе уравнение совокупности решений явно не имеет.

Проверка. Нетрудно проверить (подстановкой), что ( x= left( frac right)^2 ) — является корнем уравнения ( sqrt +sqrt =6 ). Но это уравнение равносильно исходному уравнению, значит, ( x= left( frac right)^2 ) — является корнем и исходного уравнения.
Ответ: ( x= left( frac right)^2 )

Иногда при решении иррациональных уравнений оказывается удобным ввести две новые переменные.

ПРИМЕР 5.
( sqrt[Large4normalsize] + sqrt[Large4normalsize] =2 )

Введём новые переменные: ( left<begin u=sqrt[Large4normalsize] \ v=sqrt[Large4normalsize] endright. )

Тогда уравнение примет вид (u+v=2). Но для нахождения значений двух новых переменных одного уравнения недостаточно. Возведя в четвёртую степень обе части каждого из уравнений системы, получим:
( left<begin u^4=1-x \ v^4= 15+x endright. )

Сложим уравнения последней системы: (u^4 +v^4 =16). Таким образом, для нахождения u, v мы имеем следующую симметрическую систему уравнений:
( left<begin u+v=2 \ u^4 +v^4 =16 endright. )
Решив её, находим: ( left<begin u_1=0 \ v_1 =2; endright. ) ( left<begin u_2=2 \ v_2 =0 endright. )

Таким образом, исходное уравнение свелось к следующей совокупности систем уравнений: ( left<begin sqrt[Large4normalsize] =0 \ sqrt[Large4normalsize] =2; endright. ) ( left<begin sqrt[Large4normalsize] =2 \ sqrt[Large4normalsize] =0 endright. )

Решив эту совокупность, находим: (x_1=1, ; x_2=-15 )

Проверка. Проще всего проверить найденные корни непосредственной подстановкой в заданное уравнение. Проделав это, убеждаемся, что оба значения являются корнями исходного уравнения.
Ответ: 1; -15.

ПРИМЕР 6.
( sqrt[Large3normalsize] + sqrt[Large3normalsize] = sqrt[Large3normalsize] )

Возведём обе части уравнения в куб:
( 2x+1 + 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] + 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] +6x+1 = 2x-1 Rightarrow ) ( 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] cdot (3sqrt[Large3normalsize] + sqrt[Large3normalsize] ) = -6x-3 )

Воспользовавшись исходным уравнением, заменим сумму ( sqrt[Large3normalsize] + sqrt[Large3normalsize] ) на выражение ( sqrt[Large3normalsize] ):
( 3sqrt[Large3normalsize] cdot sqrt[Large3normalsize] cdot sqrt[Large3normalsize] = -6x-3 Rightarrow )
( 3sqrt[Large3normalsize] = -2x-1 )
Возведём обе части в куб:
( (2x+1)(6x+1)(2x-1) = -(2x+1)^3 Rightarrow )
( (2x+1)((6x+1)(2x-1) + (2x+1)^2) =0 Rightarrow )
( 16x^2(2x+1) =0 Rightarrow )
( x_1= -05; ; x_2=0 )

Проверка. Подстановкой найденных значений x в исходное уравнение убеждаемся, что его корнем является только x = -0,5.
Ответ: -0,5.

Видео:Как решать иррациональные уравнения. Методы решения иррациональных уравнений. (часть 1).Скачать

2. Иррациональные неравенства

Рассмотрим иррациональное неравенство вида ( sqrt 0 ). Осталось лишь заметить, что при одновременном выполнении указанных выше условий обе части заданного иррационального неравенства неотрицательны, а потому их возведение в квадрат представляет собой равносильное преобразование неравенства.

Таким образом, иррациональное неравенство ( sqrt 0 \ f(x) 0 \ x^2-x-12 0 \ x > -12 endright. )

Получаем: ( x geqslant 4)

Ответ: ( x geqslant 4)

Рассмотрим теперь неравенство вида ( sqrt > g(x) ).

Ясно, во-первых, что его решения должны удовлетворять условию ( f(x) geqslant 0 ).
Во-вторых, замечаем, что при ( g(x) g(x) ) не вызывает сомнений.
В-третьих, замечаем, что если ( g(x) geqslant 0 ), то можно возвести в квадрат обе части заданного иррационального неравенства.

Таким образом, иррациональное неравенство ( sqrt > g(x) ) равносильно совокупности систем неравенств:
( left<begin f(x) geqslant 0 \ g(x) (g(x))^2 endright. )

Во второй системе первое неравенство является следствием третьего, его можно не писать.

Данное неравенство равносильно совокупности систем неравенств:
( left<begin x^2-x-12 geqslant 0 \ x 0 )

Преобразуем неравенство к виду ( x^2+3x-10 +3sqrt >0 ) и введём новую переменную ( y= sqrt ). Тогда последнее неравенство примет вид ( y^2+3y-10 >0 ), откуда находим, что либо (y 2).

Таким образом, задача сводится к решению совокупности двух неравенств:
( left[begin sqrt 2 endright. )

Первое неравенство не имеет решений, а из второго находим:
( x^2+3x >4 Rightarrow )
( (x+4)(x-1) >0 Rightarrow )
( x 1 )
Ответ: ( x 1 ).

🌟 Видео

Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Ограничения в иррациональных уравнениях #shorts #ЕГЭ #ОГЭ #математика #подготовкакегэ #егэматематикаСкачать

ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Система иррациональных уравнений #1Скачать

Иррациональные уравнения / 2 часть ЕГЭ профильСкачать

Иррациональные уравнения и их системы. Практическая часть. 1ч. 11 класс.Скачать

Иррациональные уравнения. 10 классСкачать

Иррациональные уравнения — часть 1Скачать

Иррациональные уравнения. Видеоурок 8. Алгебра 10 классСкачать